A compact solution of a cubic equation

Received: 15-Aug-2025, Manuscript No. PULJPAM-23-6663; Editor assigned: 17-Aug-2025, Pre QC No. PULJPAM-23-6663 (PQ); Reviewed: 30-Aug-2023 QC No. PULJPAM-23-6663; Revised: 24-Jan-2025, Manuscript No. PULJPAM-23-6663 (R); Published: 31-Jan-2025

Citation: Yoon TC. A compact solution of a cubic equation. J Pure Appl Math. 2025;9(1):1-4.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

About the Study

In this article, a simple solution of cubic equation is presented by the use of a new substitution

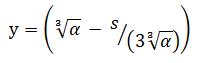
Which can replace a complicated solution presented by G. Cardano, and Francois Viete’s Vieta substitution? This paper also shows that one of the existing solution of the trigonometric function is to be changed to -cos(ÃÃÃÂ??ÂÃÂ??- π/3) instead of cos(ÃÃÃÂ??ÂÃÂ??-4π/3) due to the range limit of the inverse trigonometric function [1].

Derivation of a compact solution of a cubic equation

The solution of cubic equations is well known since an Italian mathematician Gerolamo Cardano had established. In order to replace G. Cardano's solution, I hereby settle a simple and compact substitution for an easier solution [2].

A general form of cubic equations is written as,

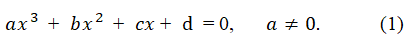
Then, a simplified equation divided both sides by the coefficient a is given as,

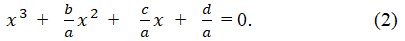
Substituting x=y-b/3a by using the Tschirnhaus transformation, we get Cardano’s basic form [3]:

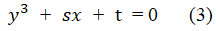
Here the coefficients s and t represent respectively.

Cardano’s basic form is:

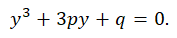
Cardano’s substitution is

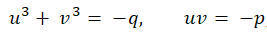
where y=(u+v) is a root of the given cubic equation.

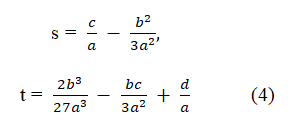
A solution of the cubic equation 1 obtained by Cardano is quite complicated because it needs several steps to get solutions. For a simplified solution, I define a new substitution analogous to Vieta's substitution, which is basically similar to Vieta’s, as is given in the form,

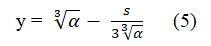
Vieta's solution of a cubic is read as follows:

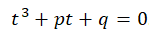
And the substitution is

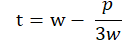
which provides

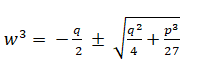
It is to be noted that this substitution provides only one solution of a cubic equation, while Cardano's and Vieta's provide three solutions. By using this substitution, we get from the equation (3),

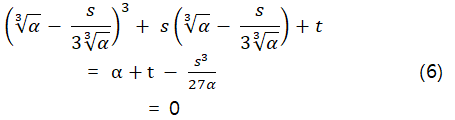
Multiplying both sides by alpha, we get a quadratic equation,

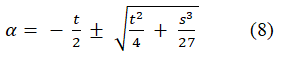
And, then we get a pair of solutions

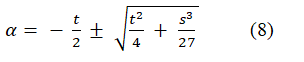
Though the resolvent quadratic equation (7) provides two roots as per the above, we can identify that they produce only one radical of the reduced cubic form (3). Substituting each α of (8) respectively, then we find the same result as follows

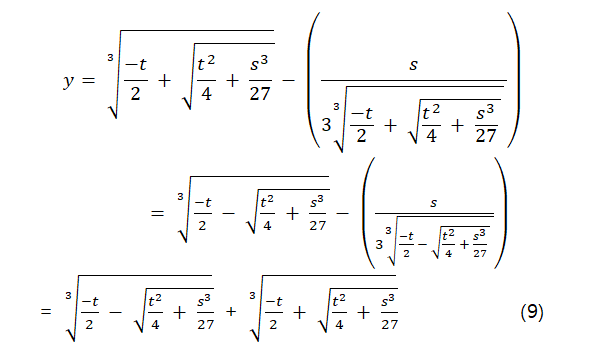
With this result, we can get the two remaining solutions by letting the above solution as y= y1 and solving the factorized quadratic equation of the right hand side

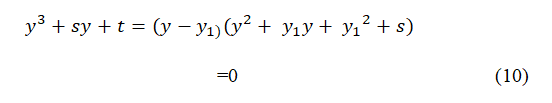
From this, we get

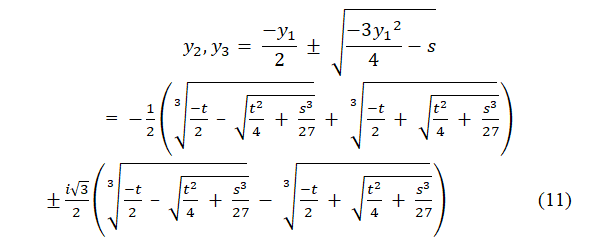
The discriminant of the cubic is given as

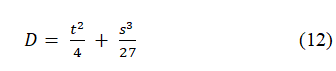
These three roots, (9) and (11) are the solutions of a cubic equation in terms of two unknown coefficients, s and t.

In case the discriminant D>0, of a cubic equation, the roots of (9) and (11) can be used as they are, because the cubic equation has one real roots and two complex conjugate. However, in case of D<0, the value in the square root of (9) is changed to an imaginary unit, in which case, it is convenient to use trigonometric functions,

In case D<0,we may eliminate the imaginary unit by using the trigonometric functions, so we can define an intermediary coefficient θ as follows,

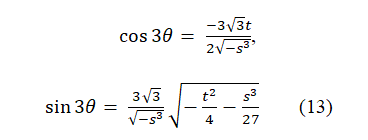
where θ is given as

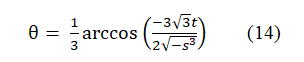
By substituting the above into the equation (9), we get the following result by using the de Moivre’s formula [4]

de Moivre’s formula proves that cosnx +isinnx = (cosx+i sinx )ⁿ.

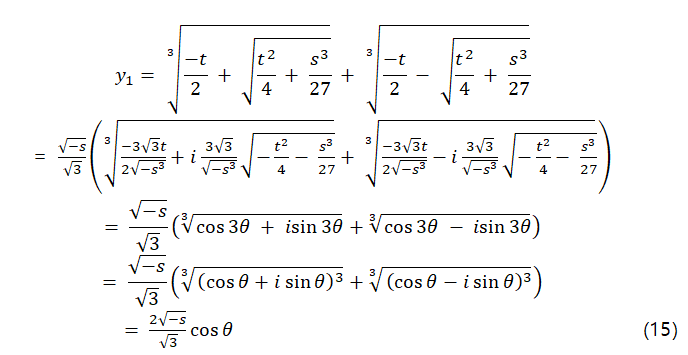
Where i represents the imaginary unit.

And the remaining two roots are given from the equation (11)

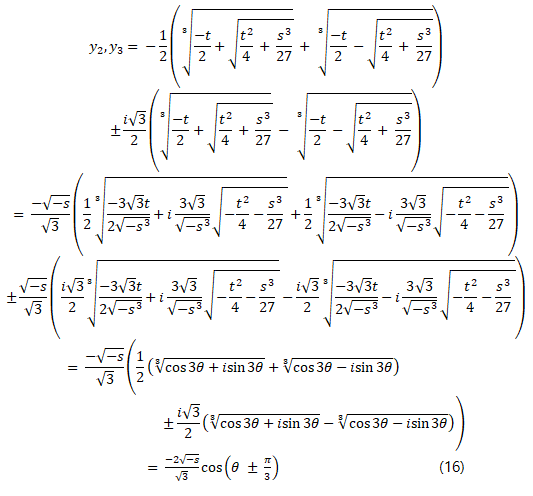
with θ[2] of (14).

The three real roots of a depressed form (t^3+pt+q=0) can be expressed as

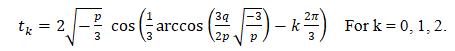
As the results, in case that the discriminant of the cubic equation (3) is D<0, the three real roots of (15) and (16) can be expressed as an inverse function of trigonometry as follows,

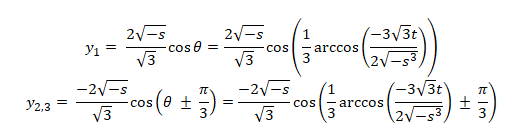
A generalized solution of a cubic equation

A general form of a cubic equation

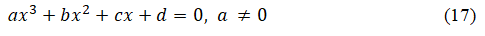
Dividing by the leading coefficient a, we get a monic cubic equation

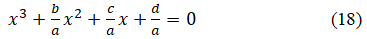
A depressed form of the above by substituting with x=y-b/3a, we get

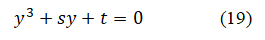
Where

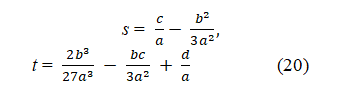
From the above (19), we get a solution of a cubic,

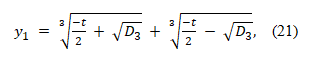
where D₃ is the discriminant of a cubic equation given as

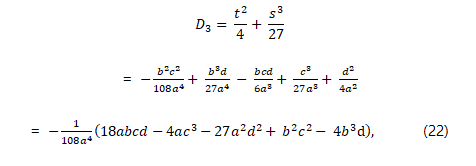
and the remaining two roots are

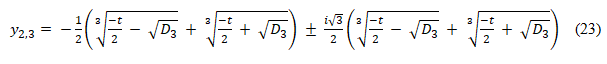
As the results, a solution of the cubic equation (18) is given as,

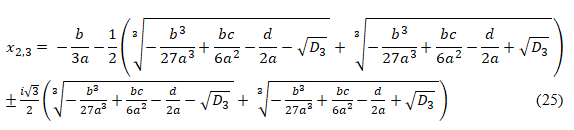
and the remaining two solutions,

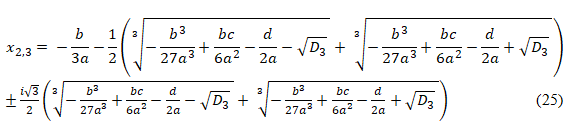
with D₃ of (22).In case D₃>0, the cubic equation has one real root of (24) and two complex conjugate of (25).

In case D₃=0, it has three real roots, two of which are equal to each other.

If D₃<0, the cubic has three different real roots.

References

1. Jeong JH. Concise Mathematics Dictionary. Changwonsa: Seoul, Korea, 1993.
2. Wikipedia contributors. "Cubic equation." Wikipedia, The Free Encyclopedia. 2015.
3. Wikipedia contributors. "Tschirnhaus transformation." Wikipedia, The Free Encyclopedia. 2015.
4. Wikipedia contributors. "De Moivre's formula." Wikipedia, The Free Encyclopedia. 2015.