A solution of a quartic equation

Received: 15-Aug-2024, Manuscript No. PULJPAM-23-6664; Editor assigned: 17-Aug-2024, Pre QC No. PULJPAM-23-6664 (PQ); Reviewed: 30-Aug-2024 QC No. PULJPAM-23-6664; Revised: 24-Jan-2025, Manuscript No. PULJPAM-23-6664 (R); Published: 31-Jan-2025

Citation: Yoon TC. A solution of a quartic equation. J Pure Appl Math. 2025;9(1): 1-3.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

This solution is equal to L. Ferrari's if we simply change the inner square root to. This article shows the shortest way to have a resolvent cubic for a quartic equation as well as the solution of a quartic equation.

Keywords

Ferrari's solution; Resolvent cubic; Solution of a quartic equation

Introduction

Derivation of a solution of a quartic equation

The solution of a quartic polynomial was discovered by Lodovico de Ferrari in 1540. Ferrari's solution is good for solving a quartic equation. This article shows a simpler way to solve the quartic equation than Ferrari [1].

A monic form of a quartic polynomial is written as

To solve a quartic, we need to get a resolvent (1) cubic. A resolvent cubic can be obtained from the above quartic equation by using the following biquadratic equation [2].

where a₁, a₀ and b₀ are arbitrary coefficients, and w is a coupling constant.

Unfolding the brackets of the equation (2) and comparing to those coefficients of the equation (1), we can find

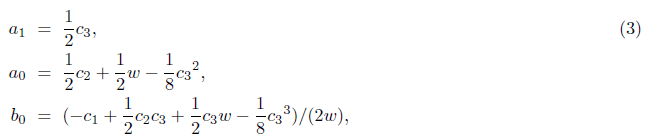
and we get the remaining resolvent equation

Solving the equation (4) with substitutions from (3), we get the resolvent cubic equation with respect to w,

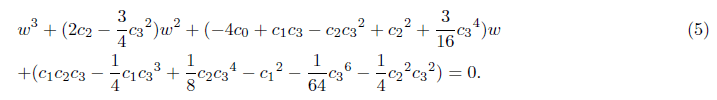
As this resolvent cubic equation is somewhat lengthy and complicated, a reduced form is applicable as follows [3-5],

where y represents

with p₁ and p₀ respectively

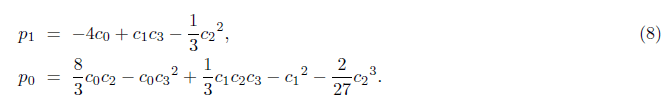
A radical solution of the cubic (6) provides

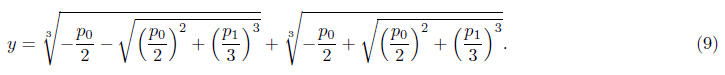
Or we can get the solution in the form of w from the equation (5) by using the equation (7)

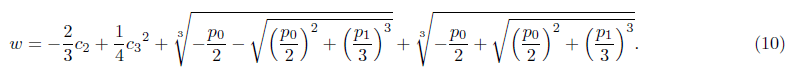
With p₁ and p₀ of (8).

It is to be noted that

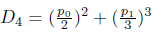
Represents the discriminant of the above quartic equation (1) and it can be expanded as below,

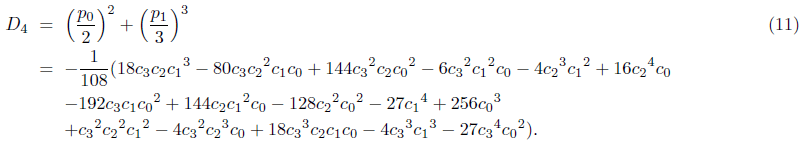
Now, we can derive out a radical solution of a quartic equation. It is convenient to deal with the equation (2) directly otherwise it is so complicated. It provides two quadratic solutions. One of them is [6]:

This gives two roots of the quadratic:

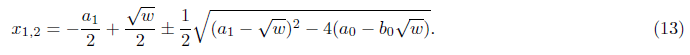
Substituting with the equations (3), we get:

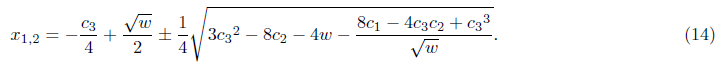
with w from (10).

These are two roots of a quartic equation (1)

Discussion

A full solution of a quartic equation

A general quartic equation is written as

Dividing by c4, we get a monic quartic equation

An intermediary biquadratic equation for a solution of a general monic quartic equation (16) is given as

For a reduced quartic, one may use the following form

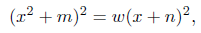
this is simply equal to the above (17) in case l = 0.

Unfolding the brackets and comparing to those coefficients of the equation (17), the coefficients are given as [7]:

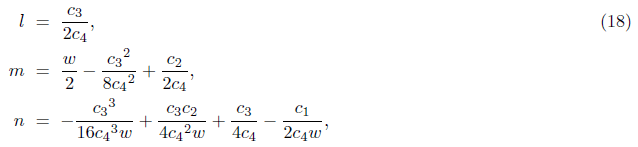
Substituting these coefficients to the equation (16), we get the resolvent cubic equation,

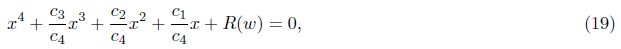
where R(w) provides the resolvent cubic with respect to w,

Where

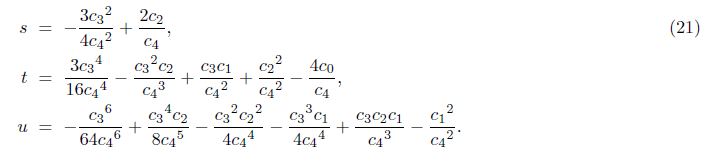
In case w=0, the biquadratic (17) simply becomes a perfect square of a quadratic equation (x²+lx+m)²=0, which includes the case l=0 when it becomes (x² + m)²=0.

Therefore the equation (17) is applicable for all quartic polynomials except when (x²+lx+m)²=0 and (x²+m)²=0, which are simply solvable by factoring. To solve the resolvent cubic equation (20), we get a reduced form by substituting with w=y-s/3,

Where,

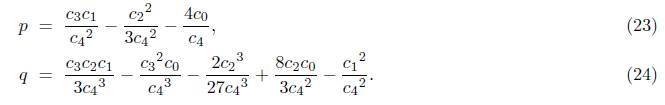
We get a solution from (22)

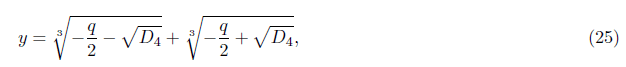
where D₄ is the discriminant of the quartic (15), which is given as follows,

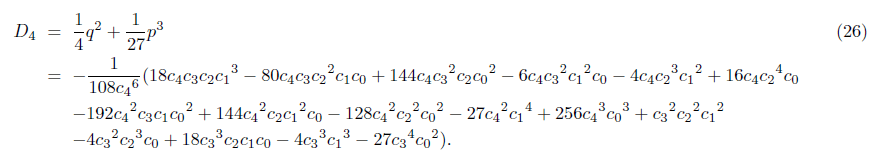
With these results, we have two quadratic equations that are two factors of the quartic equation (16)

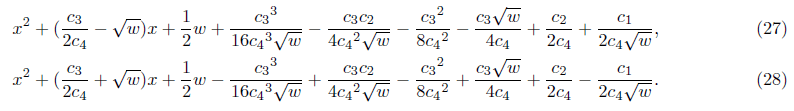
The four roots of a quartic equation are given from the above

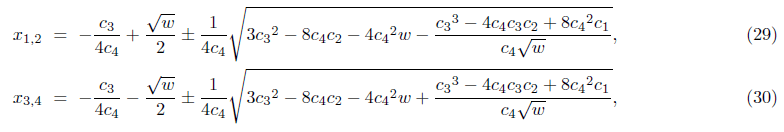
and the resolvent cubic equation of w

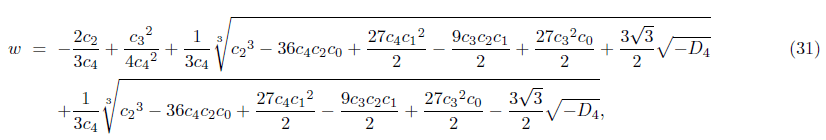
with D₄ of (26).

A full solution of a quartic equation is consisted of three parts of the equations (29), (31) and (26).

References

1. Euler L. A conjecture on the forms of the roots of equations. arXiv preprint. 2008;16

   [Google Scholar]

2. Wikipedia contributors. Quartic equation. Wikipedia, The Free Encyclopedia; 2024.
3. Wikipedia contributors. de Moivre's formula. Wikipedia, The Free Encyclopedia; 2024.
4. Wikipedia contributors. Discriminant. Wikipedia, The Free Encyclopedia; 2024.
5. Wikipedia contributors. Trigonometric functions. Wikipedia, The Free Encyclopedia; 2024.
6. Wikipedia contributors. Hyperbolic functions. Wikipedia, The Free Encyclopedia; 2024.
7. Wikipedia contributors. Quartic. Wikipedia, The Free Encyclopedia; 2021.