A solvable quintic equation

Received: 15-Aug-2023, Manuscript No. PULJPAM-23-6665; Editor assigned: 17-Aug-2023, Pre QC No. PULJPAM-23-6665 (PQ); Reviewed: 30-Aug-2023 QC No. PULJPAM-23-6665; Revised: 24-Jan-2025, Manuscript No. PULJPAM-23-6665 (R); Published: 31-Jan-2025

Citation: Yoon TC. A solvable quintic equation. J Pure Appl Math. 2025;9(1):1-4.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

This article presents a solvable quintic equation under the conditions that several coefficients of a quintic equation are restricted to become dependent on the other coefficients. We can solve a quintic equation by restricting two coecients among total four coefficients available. If a quintic equation has a quadratic factor (x²+b₁x+b₀), then we get a two simultaneous equations, which can be solved by using a sextic equation under restriction.

Keywords

Quintic equation; Coecients; Sextic equation; Quadratic factors

Introduction

de Moivre's quintic equation

A monic general quintic equation form is

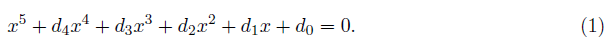
The process of solving a quintic equation is very complicated. So, we consider a reduced quantic form derived from the above equation (1) in which x is substituted with x+d₄/5, or simply d₄=0,

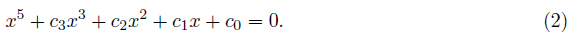
A solvable quintic equation is given from the de Moivre's quintic. de Moivre's theorem is the only formula that can solve a quintic equation by using its coefficients [1]. A solution of the de Moivre's quintic equation can be easily derived as follows. If

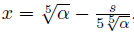
We have,

where t is the coffecient of constant term.

From the above, we get a solution of the quadratic equation with respect to α

Which provides a solution of the de Moivre's quantic

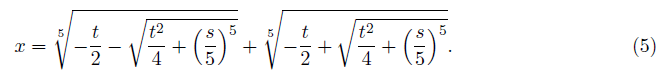
Derivation of a solvable quintic equation

A monic reduced form of a quintic equation is read as follows:

If this quintic equation is factorable into a cubic and a quadratic equation as follows,

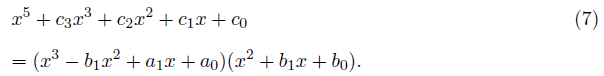
After eliminating the coefficients ai, we get two simultaneous equations with respect to b₁ and b₀.

If we get b₁ and b₀ by solving the simultaneous equations, we can get solutions of the equation (6).

To do so, developing the latter into a cubic and quadratic equation, and comparing each coefficient of nth degree of x, which is equal to each other, we can factor the quintic equation to get a solution of a quintic equation. After developing the parentheses, and comparing to each other, we get

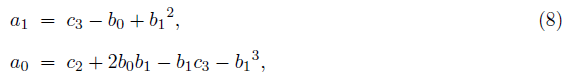
which provides with

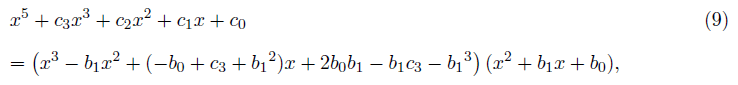
where we get two simultaneous equations with respect to b₀,

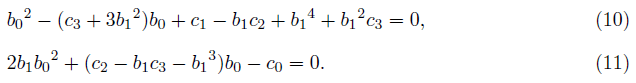
To solve these simultaneous equations (10) and (11), the resultant can be used. However, if we try to and b₁ or b₀ using the resultant, we would face more difficulties as it provides a 10^th degree equation [2]. However, the equation (6) can be solved if certain conditions are given, which has the fifth root of a quintic equation as follows.

From the equation (11), we get

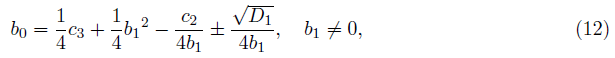
where D₁ is given as the discriminant as

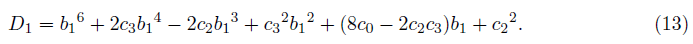
b₁ of the above can be determined by solving the sextic equation if possible.

A sextic equation to solve a quintic equation

A reduced sextic equation is read as;

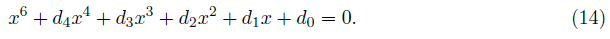
If this equation has factors both a quartic equation and a quadratic equation, we have

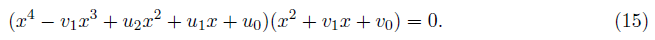
Comparing the two equations (14) and (15) after eliminating the coefficients u_i, we have

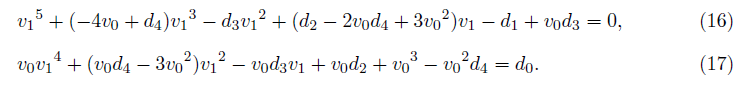
If the equation (16) becomes a de Moivre quintic, we may get v₁. Therefore, if the coefficient d₃=0 of v1² term, and the square of the coefficient of v₁ ³ term is equal to 5 times of the coefficient of v₁ term, we get

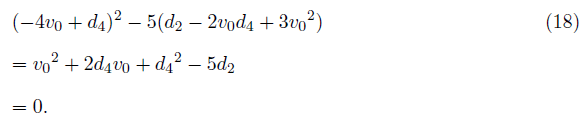
From the above, we have

One of the equation (16) provides

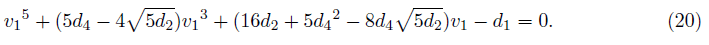
The above provides a solution

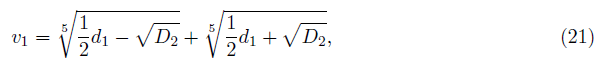
Where

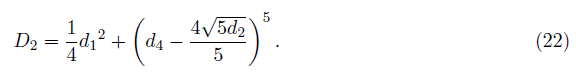
And d₀ is given from (17), which is dependent on the preceding coefficients

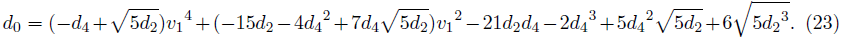
Then, we have two roots of the following quadratic factor of (15),

which provides two roots of the sextic equation (14),

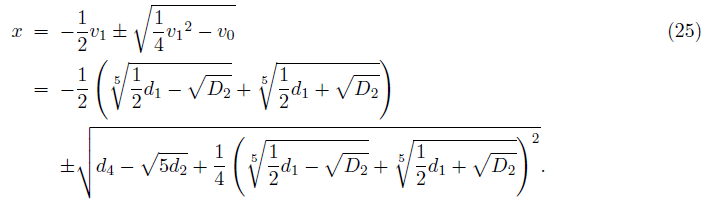
These are two roots of a sextic equation that can be factored into a quartic and a quadratic equation under restrictions [3-6].

Discussion

Solution of a solvable quintic equation

By using the above conditional solution of a sextic equation, we can get a restricted solution of the equation (13),

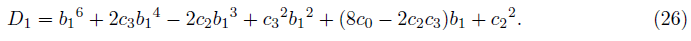
If this sextic equation has a quadratic factor,

Two unknown coefficients v₁ and v₀ are given as the simultaneous equations as follows:

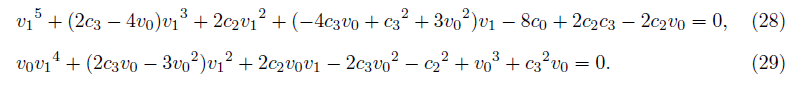
Now, we have the following results from the equation (28)

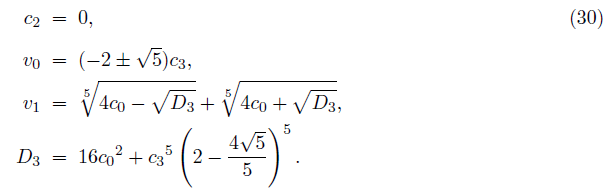
And we get two roots of the equation (27),

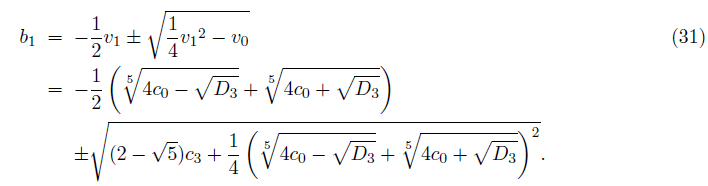
And b₀ from the equation (12) becomes

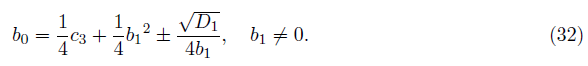
We can have two roots from the quadratic factor (x²+b_1x +b₀) of the equation (7),

where b₁ of (31) with D₃ of (30), and b₀ of (32) with D₁ of (26) respectively.

Summary and examples

A general quintic equation can be written as

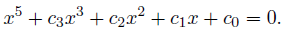
If a quintic equation is factorable with a factor of (x²+b_1x +b₀), then the quintic equation has two roots that shares two roots of the quadratic equation [7].

However, in the process of obtaining b₁ and b₀, which are the coefficients of the quadratic equation, we encounter the difficulty of solving the 10^th degree equation (decic equation). It is therefore clear that there is no general way to solve a quintic equation normally [8]. However, if certain conditions are given, b₁ and b₀ can be obtained, and thus the solution of a quintic equation can be obtained. Nevertheless, in the process of obtaining b₁ and b₀, it is difficult to solve the sextic equation, but we can find that the sextic equation can also be solved using the de Moivre quintic equation in the process of solving the sextic equation with a quadratic equation (x²+v_1x +v₀) as a factor [9]. Here, if v₁ and v₀ are obtained, then b₁ and b₀ can be obtained from them, then the roots of the quintic equation can be obtained from (x²+b_1x+b₀). To get a solvable quintic equation, the coefficient c₂ of x² term equals to zero, and then we get b₁ from (31).

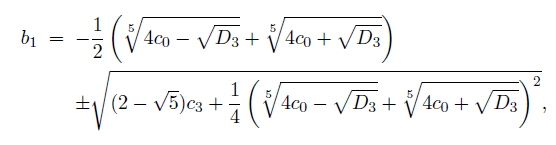
where D₃ is given from (30) as

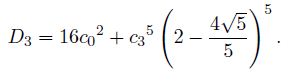
And b₀ from (32) as

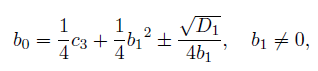
where D₁ is given from (26)

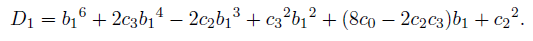
And the coefficient c₁ of x term is given from (10),

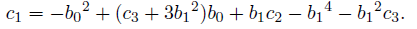
These have steps bring us solutions of a solvable quintic equation by a quadratic factor

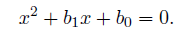
This quadratic equation provides two roots of a solvable quintic equation

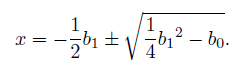
Writing down a solution of a quintic equation in a row is too lengthy, so it's much easier to just plug in each step one by one and get the result.

Since the real values obtained from arbitrary c₃ and c₀ are very complex. So for an easy example, let b₁=2, b₀=2, and c₃=-4, c₀=16, then we have c₁=12. In this case, we get the following quintic equation, which is factored into a quadratic factor

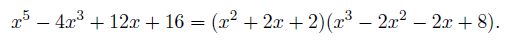
For another case, let b₁=2, c₃=0, c₀=-3, then we get D₁=16, b₀=3/2 and c₁=-1/4. The factoring is given as

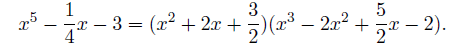
References

1. Wikipedia contributors. Quartic. Wikipedia, The Free Encyclopedia; 2021.
2. Wikipedia contributors. Sextic equation. Wikipedia, The Free Encyclopedia. 2023.
3. Wikipedia contributors. de Moivre's formula. Wikipedia, The Free Encyclopedia; 2024.
4. Wikipedia contributors. Quintic function. Wikipedia, The Free Encyclopedia; 2024.
5. Story of Mathematics. de Moivre's theorem-fomulas, explanation, and examples. 2022.
6. Wolfram Mathworld. Sextic equation. 2022.
7. Titus Piezas. An easy way to solve the solvable quintic using two sextics. Oocities. 2016.
8. Wolfram Mathworld. Quintic equation. 2022.
9. Wolfram Mathworld. De Moivre's Quintic. 2022.