An elementary proof of Fermat's last theorem v. 1.4

Received: 17-Jan-2024, Manuscript No. PULJPAM-24-6920; Editor assigned: 19-Jan-2024, Pre QC No. PULJPAM-24-6920 (PQ); Reviewed: 02-Feb-2024 QC No. PULJPAM-24-6920; Revised: 18-Mar-2025, Manuscript No. PULJPAM-24-6920 (R); Published: 25-Mar-2025

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

In this present paper we will show you an elementary proof of the Fermat’s Last Theorem, that is “too large to fit in the margin”, for the general case xⁿ + yⁿ=zⁿ. First we begin showing you the cases n=2, n=3 and n=4 to familiarize with the general solution n ∈ ℕ, n ≥ 3.

Keywords

Fermat; Theorem; Elementary; Proof; Number theory; Fermat’s last theorem

Introduction

Around the year 1637, Pierre de Fermat, a lawyer and an amateur mathematician, was reading the Diophantus book ”Arithmetica” and wrote in the margin the next words:

”Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.”

Its translation is as follows:

”It is impossible to separate a cube into two cubes, or a fourth power into two fourth powers, or in general, any power higher than the second, into two like powers. I have discovered a truly marvelous proof of this, which this margin is too narrow to contain” [1]. Mathematically speaking, it says: There are no solutions for the diophantine equation xⁿ+yⁿ = zn with x, y, z, n ∈ â?? and n ≥ 3, except the trivial solutions x=0, y=0 and z=0.

For centuries that proposition was challenging for the mathematicians and there is a lot of literature about its development. We suggest the reading of Paulo Ribemboim [2]. On the year 1995, Andrew John Wiles became to the proof of the Fermat’s last theorem with modular elliptic curves theory and solving the Taniyama-Shimura-Weil conjecture [3]. He was awarded with the Abel Prize in 2016 and the Copley Medal in 2017.

In the dawn of October 8 in 2023 we was thinking, relaxed at the moment of almost sleeping, about how to solve the problem of Fermat’s last theorem in an elementary way. Trying an easy reconfiguration of the equation x²+y²=z², we became to the solution of the case n=2. In the next afternoon we proceeded to write the proof and calculate its correctness. Later on October 9 of 2023 we discovered the cases n=3, x³+y³ ≠ z³ and n=4, x⁴+y⁴ ≠ z⁴ by the same way. Later on October 9 of 2023 we arrived to the sketch of the general case xⁿ+yⁿ ≠ zⁿ, n ∈ N, n ≥ 3. We show you the results for your enjoyment [4-5].

Description

Proof of the case N=2, X²+Y²=Z² and Pythagorean triplets

Theorem 1

Let be x, y, z ∈ Z, x ≠ 0, y ≠ 0, z ≠ 0, z>x, z>y.

x²+y²=z²

We can make every primitive Pythagorean triplet, (x, y, z), as follows if k=1, 2, 3... and c=1, 2, 3...

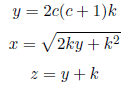
if k=1, 2, 3... and c = 1, 2, 3..

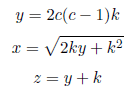
the multiples of the Pythagorean triplets can be made only by multiplying the three numbers (mx,my,mz).

Proof: We begin with the proposed equation to test its validity

x²+y²=z²

let us rewrite this as

x²=z²−y²=(z−y)(z+y)

Setting z=y+k, k=1, 2, 3... , z > y, we have

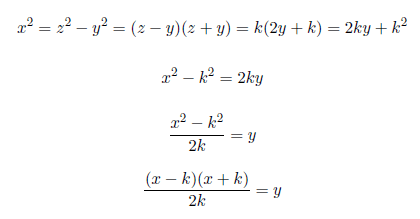
Case 1: To find the value of k, we use the above equation

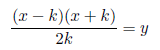
Setting x−k=2ck, c=1, 2, 3... , we have x=(2c+1)k Substituting x=(2c+1)k in the above equation we have

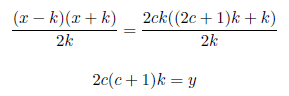
y is a whole number because the left side is a whole number.

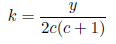
k is a whole number because we can choose y being a multiple of 2c(c+1).

Case 2: Coming back with the above equation, to find the value of k

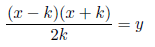
Setting x+k=2ck, c=1, 2, 3... , we have x=(2c−1)k. Substituting x=(2c−1)k in the above equation we have

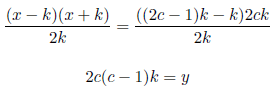
y is a whole number because the left side is a natural number.

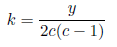
k is a whole number because we can choose y being a multiple of 2c(c−1).

Conclusion: As the proposed equation depends on k being a whole number, remember that z=y+k and k is in fact a whole number that we can conveniently choose, we conclude that

x²+y²=z²

Addendum: We can make every primitive Pythagorean triplet, (x, y, z), as follows if k= , 2, 3... and c=1, 2, 3...

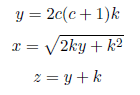
if k=1, 2, 3... and c=1, 2, 3...

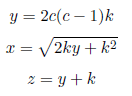
The multiples of the Pythagorean triplets can be made only by multiplying the three numbers (mx,my,mz).

Quod Erat Demonstrandum (QED)

Proof of the case n=3, x³ + y³/= z³

Theorem 2:

Let be x, y, z ∈ Z, x ≠ 0, y ≠ 0, z ≠ 0, z > x, z > y.

x³+y³ ≠ z³

Proof: We begin with the proposed equation to test its validity

x³+y³=z³

Let us rewrite this as

x³=z³−y³=(z−y)(z²+zy+y²)

Setting z=y+k, k=1, 2, 3... , z>y, we have

x³=z³−y³=(z−y)(z²+zy+y²)=k(3y²+3ky +k²)=3ky²+3k²y+k³

x³−k³=3ky²+3k²y

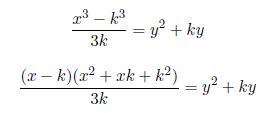
Case 1: To find the value of k, we use the above equation

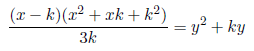
Setting x−k=3ck, c=1, 2, 3... , we have x=(3c+1)k. Substituting x=(3c+1)k in the above equation we have

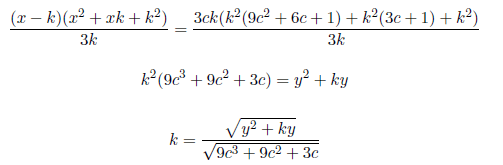
k is not a whole number because the numerator is not a multiple of the denominator, remember that z=y+k.

Case 2: Coming back with the above equation, to find the value of k

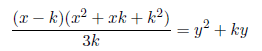
Setting x²+xk+k²=3ck, c=1, 2, 3... , we have

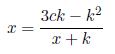
Substituting

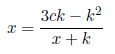
in the above equation we have

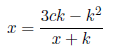
k is not a whole number because the numerator is not a multiple of the denominator, remember that z=y + k.

Conclusion: As the proposed equation depends on k being a whole number, remember that z=y+k, and k is not a whole number, we conclude that

x³+y³ ≠ z³

Quod Erat Demonstrandum (QED).

Proof of the case n=4, x⁴+y⁴ ≠ z⁴

Theorem 3: Let be x, y, z ∈ Z, x ≠ 0, y ≠ 0, z ≠ 0, z > x, z > y.

x⁴+y⁴ ≠ z⁴

Proof: We begin with the proposed equation to test its validity

x⁴+y⁴=z⁴

Let us rewrite this as

x⁴=z⁴−y⁴=(z−y)(z³+z²y+zy²+y³)

Setting z=y+k, k=1, 2, 3... , z > y, we have

x⁴=z⁴−y⁴=(z−y)(z³+z²y+zy²+y³)=k(4y³+6ky²+4k²y+k³)=4ky³+6k2y²+4k³y+k⁴

x⁴−k⁴=4ky³+6k²y²+4k³y

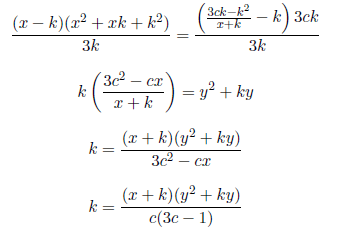
Case 1: To find the value of k, we use the above equation

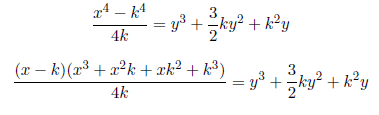
Setting x−k=4ck, c=1, 2, 3... , we have x=(4c+1)k. Substituting x=(4c+1)k in the above equation we have

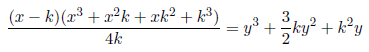
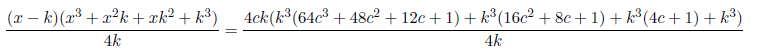
k is not a whole number because the numerator is not a multiple of the denominator, remember that z=y+k.

Case 2: Coming back with the above equation, to find the value of k

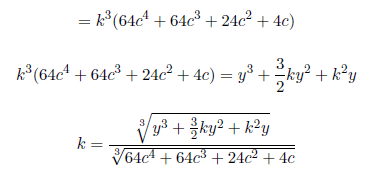
k is not a whole number because the numerator is not a multiple of the denominator, remember that z=y+k.

Conclusion: As the proposed equation depends on k being a whole number, remember that z=y+k, and k is not a whole number, we conclude that

x⁴+y⁴ ≠ z⁴

Quod Erat Demonstrandum (QED).

Proof of the general case xn+yn ≠ zn

Theorem 4:

Let be x, y, z ∈ Z, x ≠ 0, y ≠ 0, z ≠ 0, z>x, z>y, n ∈ N, n ≥ 3.

xⁿ+yⁿ ≠ zⁿ

Proof: We begin with the proposed equation to test its validity

xⁿ+yⁿ=zⁿ

Let us rewrite this as

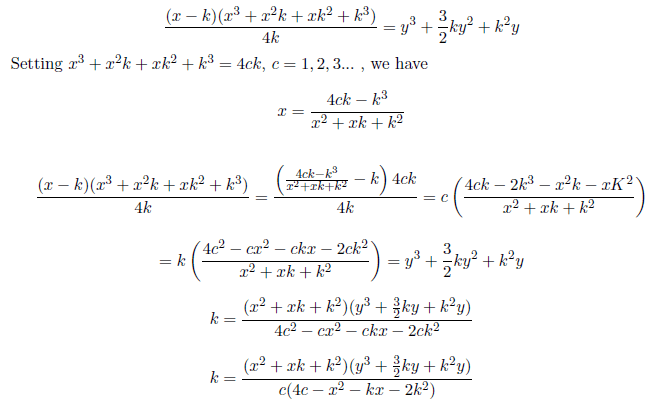
Setting z=y+k, k=1, 2, 3... , z > y, we have

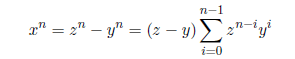
We can rearrange the sums, in order to simplify the double sum into only one sum of variables

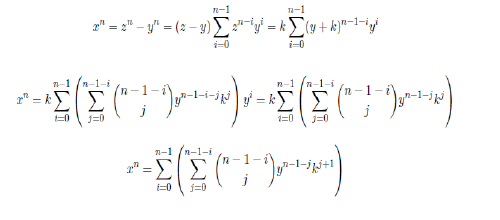
in the next way:

Setting i=0

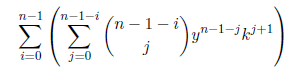
Setting i=1

+

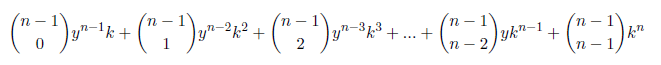
Setting i=n–2

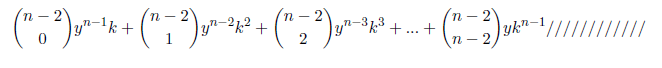
Setting i=n–1

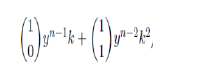
Summing by columns we have

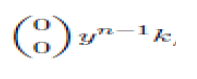
Returning to the main relations we have

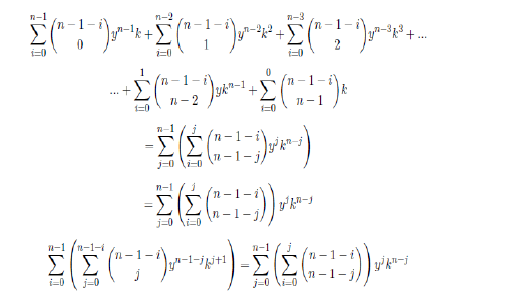
Now we can rearrange taking one element of the sum from the above formula

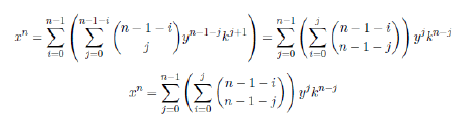
Case 1: To find the value of k, we use the above equation

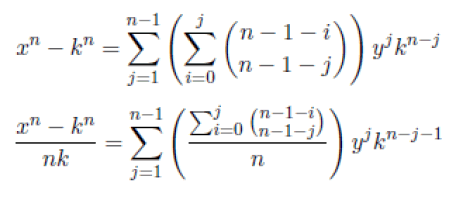
Setting x−k=cnk, c=1, 2, 3... , we have x=(cn+1)k. Substituting x=(cn+1)k in the above equation we have

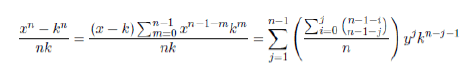
k is not a whole number because the numerator is not a multiple of the denominator, remember that z=y+k.

Case 2: Coming back with the above equation, to find the value of k

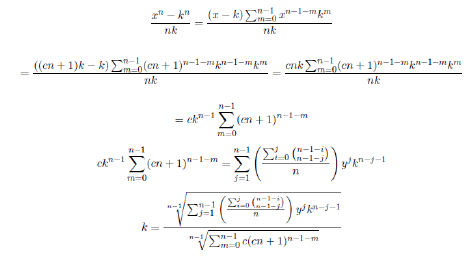
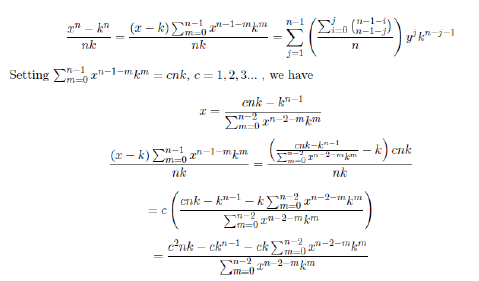
k is not a whole number because the numerator is not a multiple of the denominator, remember that z=y+k.

Conclusion

As the proposed equation depends on k being a whole number, remember that z = y +k, and k is not a whole number, we conclude that

xⁿ+yⁿ ≠ zⁿ

if n ≥ 3.

Quod Erat Demonstrandum (QED).

Acknowledgement

We are thankful with Jean-Marc Deshouillers (jeanmarc. deshouillers@math.u-bordeaux.fr) for pointing out some mistake in our previous reasoning that we have already corrected.

References

1. Heath TL. Diophantus of Alexandria: A study in the history of Greek algebra. University Press; 1910.

   [Google Scholar]

2. Ribenboim P. 13 lectures on Fermat's last theorem. Springer Science and Business Media; 1979.

   [Google Scholar]

3. Wiles A. Modular elliptic curves and Fermat's last theorem. Ann Math. 1995;141(3):443-551.

   [Google Scholar]

4. Nag BB. An elementary proof of Fermat’s Last Theorem for epsilons. Adv Pure Math. 2021;11(8):735-40.

   [Google Scholar]

5. Karmakar SB. An elementary proof of Fermat’s last theorem for all even exponents. J Math Cryptol. 2020;14(1):139-42.

   [Google Scholar]