Brake power required to prevent vehicle’s obstruction with a steadfast obstacle probabilistic approach
Received: 28-Jun-2021 Accepted Date: Jul 02, 2021; Published: 11-Jul-2021, DOI: 10.37532/2752-8081.21.5.31
Citation: E Suhir. Brake power required to prevent vehicle’s obstruction with a steadfast obstacle: probabilistic approach. J Pur Appl Math. 2021; 5(4):51:52.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
A probabilistic approach is applied to assess the required brake power to avoid obstruction with a suddenly detected steadfast obstacle in front of the moving vehicle. The obtained results can be used to select, on the design stage, the level of this power for extraordinary situations of the type in question.
The estimated results are presented in tables and charts and conclusions have been drawn for future precautionary measures.
Keywords
Power; Brake; Steadfast; Research approach
Introduction
The brake system, weather electromagnetic, frictional or hydraulic, is supposed to absorb energy from a moving vehicle and is therefore a must on all types of vehicles [1,2]. The characteristics of a brake system include, as is known, peak force, continuous power dissipation, fade, smoothness, power, pedal feel, drag, durability, weight, and even the level of noise. This analysis, however, is limited to the role and the required power. As is known, two major phases of the stopping process are being distinguished [1-4]: the first one, the pre-braking phase, includes the perception (decision making) time and the reaction time and is characterized by the more or less constant speed; the second one, when actual braking takes place, is characterized by a more or less constant deceleration, and it is at this phase, when an adequate brake power is important. In the analysis that follows a probabilistic approach is applied to assess the required brake power to avoid vehicle’s obstruction with a suddenly detected steadfast obstacle. A situation, when the only way to avoid an accident is by using brakes (see, e,g., Figure 1), is addressed. The objective of the analysis is to establish the never-zero probability of the possible obstruction depending on the level of the brake system’s power. The obtained results can be used to select this level, considering extraordinary, but always possible, situations of the type in question.
Analysis
The vehicle’s kinetic energy 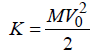 at the beginning of the braking time of the duration is expected to be absorbed during this time by the braking system to assure safe outcome of the situation. This means that the system should possess the power of
at the beginning of the braking time of the duration is expected to be absorbed during this time by the braking system to assure safe outcome of the situation. This means that the system should possess the power of 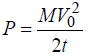 to do the job. Here M is the vehicle’s mass and V0 is its speed at the beginning of the braking time. This time can be found for the given braking distance and the initial speed V0 as
to do the job. Here M is the vehicle’s mass and V0 is its speed at the beginning of the braking time. This time can be found for the given braking distance and the initial speed V0 as 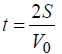 , and therefore
, and therefore
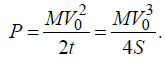 (1)
(1)
No wonder that the existing safety regulations require that in hazardous situations of the type in question the initial driving speed V0 should be kept as low as possible.
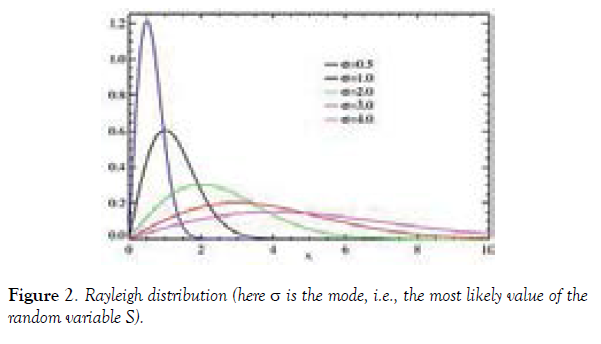
The mass of the car and its initial velocity are usually known reasonably well compared to the available braking distance S, even if radars (“radio detection and ranging”) and/or lidars (optical radars: “laser imaging, detection, and ranging”) are employed. In our analysis this distance is treated therefore as a random variable. We assume that it is distributed in accordance with the Rayleigh law (Figure 2):
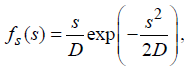 (2)
(2)
where the notation
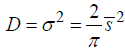 (3)
(3)
is used. Here σ is the mode (the most likely value) of the distance S and s̄ is its mean value. The variance D* of the distribution (2) is related to the D value as 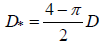 . The rationale behind such an assumption is that the probabilities are zero for both zero and very large braking distances S, that relatively low distances S are much more likely and, as far as this analysis is concerned, are of a greater interest than large distances, and because of that the physically meaningful probability density distribution function fs(s) for the distance S should be heavily skewed towards low S values. Rayleigh distribution is the simplest one that possesses these physically meaningful properties.
. The rationale behind such an assumption is that the probabilities are zero for both zero and very large braking distances S, that relatively low distances S are much more likely and, as far as this analysis is concerned, are of a greater interest than large distances, and because of that the physically meaningful probability density distribution function fs(s) for the distance S should be heavily skewed towards low S values. Rayleigh distribution is the simplest one that possesses these physically meaningful properties.
Treating the random braking power Pas a nonrandom function of the random variable (see, e.g., [5]), we obtain the following expression for the probability density function of the braking power:
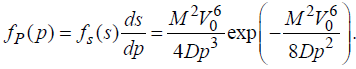 (4)
(4)
This power should be above a certain non-random level (threshold) to avoid obstruction. The probability
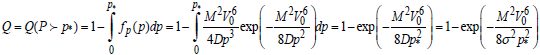 (5)
(5)
could be viewed as the probability of the inability of the braking system to do its job, i.e., as the probability of the obstruction. As evident from this formula, the probability of hitting the obstacle is lower for a lower mass M of the vehicle, for a lower initial speed V0, for a higher most likely available distance σ and for a higher power of the braking system. The formula (5) indicates also that the level of the speed V0 is particularly critical. We would like to emphasize that it is a simplified treatment of the problem and is aimed at the demonstration of the usefulness of the probabilistic approach. Many important factors are not taken into account: the road and tire conditions, the role of the human factor, the friction between the tires and the road (as is known, for rubber tires, the coefficient of friction decreases as the mass of the car increases), rubber temperature, weather conditions, vehicle’s air drag, etc.
Let, e.g., the speed at the beginning of the braking distance for a heavy truck that weighs 30,000 lb =13,608kg (its mass is M = 1387.2kgxs2xm−1) and whose braking system’s horse-power is p =1300hp = 97500kgm / s, is V0 = 50mph = 22.351m / s . Then the formula (5) yields:
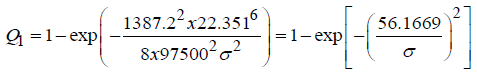
If the initial velocity is only then
The calculated data for different braking distances are shown below in Table 1.
| σ,m | 50 | 75 | 100 | 150 | 200 | 250 | 300 | 350 |
|---|---|---|---|---|---|---|---|---|
| Q1 | 0.7169 | 0.4293 | 0.2706 | 0.1308 | 0.0758 | 0.0492 | 0.0344 | 0.0254 |
| Q2 | 0.2816 | 0.1367 | 0.0794 | 0.0361 | 0.0205 | 0.0131 | 0.00914 | 0.00673 |
Table 1: Data for different braking distances.
As evident from these data, by slowing down the car in anticipation of a hazardous situation, one could reduce dramatically the likelihood of the accident.
Conclusion
A probabilistic approach is applied to assess the required brake power to avoid vehicle’s obstruction with a suddenly detected steadfast obstacle in front of the moving car. The obtained results can be used to establish the power of the brake system to possibly avoid obstruction in extraordinary situations of the type in question.
REFERENCES
- Taoka GT. Brake reaction times of unalerted drivers. ITE journal. 1989;59(3):19-21.
- Taoka GT. Brake reaction times of unalerted drivers. ITE journal. 1989;59(3):19-21.
- Suhir E and Paul G.Avoiding Collision in an Automated Driving Situation. Theor Issues Ergon Sci, 2020.
- Michel Sidibe.Giving Power to Couples to End the AIDS Epidemic. A Joint United Nations Programme on HIV/AIDS.2012
- Suhir E, Paul G, Kaindl H. Towards probabilistic analysis of humansystem integration in automated driving. InInternational Conference on Intelligent Human Systems Integration 2020(pp. 9-14). Springer, Cham.
- Suhir E, Rafanelli AJ. Applied probability for engineers and scientists 1997.