Commutator properties and relative theories in communication with solvable groups

Received: 18-Jul-2018 Accepted Date: Aug 17, 2018; Published: 23-Aug-2018

Citation: Md Taufiq Nasseef. Commutator properties and relative theories in communication with solvable groups. J Pur Appl Math. 2018;2(2):14-21.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

The study of groups arose from the theory equations; more specifically form the attempt to find roots of a polynomial in terms of its coefficients, early in the 19^th century. The theory of groups itself, which had already been applied in almost all branches of Mathematics, has developed in many different directions. It becomes of prime importance in many Mathematical disciplines. Here, I have studied an essential part of groups called Commutators related to solvable groups. In this study, I have discussed Commutator properties and intend to present some relative noteworthy theorems of commutators in connection with solvable groups. I have assumed the group G to be finite group throughout the whole work.

Keywords

Finite group; Commutator; Commutator subgroup; Solvable groups

Definition of a commutator

(a) Let G be a group. If a and b are elements of a group G, then ab=bac for some c∈G. If a and b commute, then, of course, c=e. In general c ≠ e and c = a⁻¹b⁻¹ab . An element of this form is called a commutator and is usually denoted by (a,b).

(b) We also define commutators of higher order by the recursive rule:

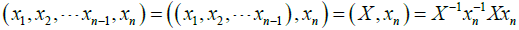[1]

Where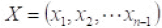

These are called simple commutators.

(c) The set of all elements which can be obtained by successive commutation are called complex commutators.

(d) Let G be a group. Let A and B be subgroups by the notation (A,B), we mean the group generated by all commutators. (a,b) with a∈A, b∈B.

(e) If A₁, A₂,……A_n-1, An are subgroups of a group G, then we define (A₁,A₂,……A_n-1,An) = ((A₁,A₂,……A_n-1),An) [2]

(f) We shall represent conjugation by an exponent ax=x^-1ax where x is fixed in G and for all x∈G. [1]

Definition of commutator subgroup

Let G be a group. Let us denote by the subgroup generated by the set of all commutators (a,b )= a-1b-1 of G, for all a,b ∈G, then is called the commutator subgroup of G′ [1,7-11].

Note: G′ is normal in G.

Some properties of commutators

Note: Let x,y ∈G then (x,y)=e the identity of G if and only if xy = yx, the proof follows directly from the definition of a commutation [1-11].

Property^-1: Let xy∈G be elements of a group G, the (y,x) = (x,y)^-1 [3]

Proof:

L.H.S: (y,x) = y^-1x^-1yx = (x^-1y^-1xy)^-1 = y^-1x^-1yx

Hence, (y,x) = (x,y)^-1

Property-2:

Let x,y,z ∈G be elements of a group G then

(xy,z) = (x,z)^y(y,z) = (x,z)(x,z,y)(y,z) [4]

Proof:

Consider, (xy,z) = (xy)^-1z^-1(xy)^z = y^-1x^-1z^-1xyz

Consider, (x,z)^y(y,z) = y^-1(x,z)^y(y,z)

= y^-1x^-1z^-1xzyy^-1z^-1yz

= y^-1x^-1z^-1xyz

Again, (x,z)(x,z,y)(y,z)

= x^-1z^-1xz(x,z)^-1y^-1(x,z)^yy^-1z^-1yz

= x^-1z^-1xzz^-1x^-1zxy^-1x^-1z^-1xzyy^-1z^-1yz

= y^-1x^-1z^-1xyz

Hence, (xy,z) = (x,z)^y(y,z) = (x,z)(x,z,y)(y,z)

Property-3: Let x,y,z be elements of a group G. Then

(x,yz)=(x,z)(x,y)^z=(x,z)(x,y)(x,y,z) [5]

Proof:

Consider, (x,yz) = x^-1(yz)^-1xyz = x^-1z^-1y^-1xyz

Consider, (x,z)(x,y)^z = (x,z)^z-1(x,y)^z

= x^-1z^-1xzz^-1x^-1y^-1xyz

= x^-1z^-1y^-1xyz

Again (x,z)(x,y)(x,y,z) = x^-1z^-1xzx^-1y^-1xyx^-1(y,z)^-1x(y,z)

=x^-1z^-1xzx^-1y^-1xyy^-1x^-1yxz^-1x^-1y^-1xyz

= x^-1z^-1y^-1xyz

Hence, (x,yz) = (x,z)(x,y)^z = (x,z)(x,y)(x,y,z)

Property-4:

Let x,y,z be elements of a group G, Then

(x,y^-1,z)^y(y,z^-1,x)^z(z,x^-1,y)^x = e, the identity of G. [6]

Proof:

Consider (x,y^-1,z)^y = y^-1(x,y^-1,z)^y

= y^-1(x,y^-1)^-1z^-1(x,y^-1)^zy

= y^-1yx^-1yxz^-1x^-1yxy^-1zy

= x^-1yxz^-1x^-1y xy^-1zy (a)

Similarly, (y,z^-1,x)^z = z^-1(y,z^-1,x)^z

= z^-1(y,z^-1)^-1x^-1(y,z^-1)^xz

= z^-1zy^-1z^-1yx^-1y^-1zyz^-1xz

=y^-1z^-1yx^-1y^-1zyz^-1xz (b) Again,

(z,x^-1,y)^x = x^-1(z,x^-1,y)^x

= x^-1(z,x^-1)^-1y^-1(z,x^-1)^yx

= x^-1xz^-1x^-1zy^-1z^-1xzx^-1yx

=z^-1x^-1zy^-1z^-1xzx^-1yx (c)

Now, Combining (a),(b),(c), we get

x^-1y^-1xz^-1x^-1yxy^-1zy y^-1z^-1yx^-1y^-1zyz^-1xz z^-1x^-1zy^-1z^-1xzx^-1yx =e(identity)

Hence, (x,y^-1,z)^y(y,z^-1,x)^z(z,x^-1,y)^x = e, the identity of G.

Property-5:

Let x,y,z be elements of a group G, then

(x,y,z)(y,z,x)(z,x,y)=(y,x)(z,x)(z,y)^x(x,y)(x,z)^y(y,z)^x(x,z)(z,x)^y [7]

Proof:

L.H.S. (x,y,z)(y,z,x)(z,x,y)

= (x,y)^-1z^-1(x,y)^z(y,z)^-1x^-1(y,z)^x(z,x)^-1y^-1(z,x)^y

= y^-1x^-1yxz^-1x^-1y^-1xyzz^-1y^-1zyx^-1y^-1z^-1yzxx^-1z^-1xzy^-1z^-1x^-1zxy

= y^-1x^-1yxz^-1x^-1y^-1xzyx^-1y^-1z^-1yxzy^-1z^-1x^-1zxy

R.H.S. (y,x)(z,x)(z,y)^x(x,y)(x,z)^y(y,z)^x(x,z)(z,x)^y

= (y,x)(z,x)^x-1(z,y)^x(x,y)^y-1(x,z)^yx-1(y,z)^x(x,z)^y-1(z,x)^y

= y^-1x^-1yxz^-1x^-1zxx^-1z^-1y^-1zyxx^-1y^-1xyy^-1x^-1z^-1xzyx^-1y^-1z^-1yzxx^-1z^-1xzy^-1z^-1x^-1zxy

= y^-1x^-1yxz^-1x^-1y^-1xzyx^-1y^-1z^-1yxzy^-1z^-1x^-1zxy

Therefore, L.H.S. = R.H.S

Property-6:

Let x,y,z be elements of a group G, then

(x,y,z) = ((z,x^-1,y^-1)^xy)^-1((y^-1,z^-1,x)^zy)^-1 [8]

Proof:

L.H.S (x,y,z) = (x,y)^-1z^-1(x,y)^z

= y^-1x^-1yxz^-1 x^-1y^-1xyz

R.H.S. ((z,x^-1,y^-1)^xy)^-1 = [(xy)^-1(z,x^-1,y^-1)^xy)]^-1

= [y^-1x^-1(z,x^-1)^-1(y^-1)^-1(z,x^-1)^y-1xy]^-1

= (y^-1x^-1xz^-1x^-1zyz^-1xzx^-1y^-1xy)^-1

= y^-1x^-1yxz^-1x^-1zy^-1z^-1xzx^-1xy

=y^-1x^-1yxz^-1x^-1zy^-1z^-1xzy (a)

Again,

((y^-1,z^-1,x)^zy)^-1 = [(zy)^-1(y^-1,z^-1,x)^zy]^-1

= [y^-1z^-1(y^-1,z^-1)^-1x^-1(y^-1,z^-1)^xzy]^-1

= [y^-1z^-1zyz^-1y^-1x^-1 yzy^-1z^-1xzy]^-1

= [z^-1y^-1x^-1 yzy^-1z^-1xzy]^-1

= y^-1z^-1x^-1zyz^-1y^-1xyz (b)

Combining (a) and (b) we get

y^-1x^-1yxz^-1x^-1zy^-1z^-1xzyy^-1z^-1x^-1zyz^-1y^-1xyz = y^-1x^-1yxz^-1x^-1y^-1xyz

Hence, L.H.S=R.H.S and the proof follows:

Property-7:

Let x,y be elements of a group G and suppose that z = (x,y) commutes with both x and y

Then (i)(xⁱ,y^j) = z^ij for all j [9]

(ii) 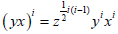for all I [10]

Proof:

Since x^-1y^-1xy = z, then we have y^-1xy = xz where y^-1xⁱy = (y^-1xy)ⁱ = (xz)ⁱ = xⁱzⁱ as x and z commute. Conjugating by y which gives that

y^-1(y^-1xⁱy)^y = y^-1 (xⁱzⁱ)^y = (xⁱzⁱ)^zi = xⁱz²ⁱ

as y and z commute.

Repeating this argument j times. We conclude that

y^-jxⁱy^j = xⁱz^ij and (xⁱ,y^j) = z^ij

Again, (ii) holds, for j=1, assuming the result for (i-1), we have

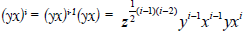
Since, by then follows at once, that is,

Hence 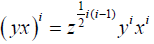for all i

Property-8:

Let x,y,z be element of a group G then

(i) If is commutes with z and if (x,G) is abelian then

(x,y,z)=(x,z,y) [11]

(ii) If (x,y) commutes with both x and y then

(xy^-1)^-1=(x^-1,y)=(x,y^-1) [12]

Proof:

First (x,y,z ) = (x,y)^-1z^-1(x,y)(z)

= y^-1x^-1yxz^-1x^-1y^-1xyz

= x^-1(xy^-1x^-1y)(xz^-1x^-1z)(z^-1y^-1xyz)

Furthermore, xy^-1xy = (x^-1,y) = (x^m,y) for some positive integer m, we conclude easily by p-2 that (x^m,y)∈(x,G) .

Thus, xy^-1x^-1y, and likewise xz^-1x^-1z lies in (x,G).

Hence, by hypothesis these two elements commute. It follows, therefore, that

(x,y,z) = x^-1(xy^-1x^-1y)(xz^-1x^-1z)(z^-1y^-1xyz)

Since, y and z commute by assumption, this reduces to

(x,y,z) = z^-1x^-1zxy^-1x^-1z^-1xzy

= (x,z,y)

which proves ⁽ⁱ⁾

We have, e = (xx^-1,y )= (x,y)(x,y,x^-1)(x^-1,y)

But, (x,y,x^-1) = ((x,y),x^-1) and (x,y) commute with x by hypothesis, whence (x,y,x^-1) = e

Hence, e = (x,y)(x^-1,y) and consequently, (x,y)^-1 = (x^-1,y)

Similarly, by p-3, we obtain(x,y)^-1 = (x,y^-1) by (i ) holds.

Some theorems on commutators

Theorem-1: Let G be a group and G′ be the commutator subgroup of G, then G′ is both characteristic and fully invariant subgroups of G.

Proof:

Let α be arbitrary automorphism of G.

Let (x,y) = x^-1y^-1xy for all x,y∈G

Then

α (x^-1y^-1xy) = α (x^-1)α (y^-1)α (x)α (y)∈G′ ,

since α is the homomorphism of G

Hence, G′ is characteristic subgroup of G. Again, be an arbitrary endomorphism of G. Then G′ will be invariant by as before. Hence, G′ is also fully invariant subgroup G.

Theorem-2: Let G′ be a commutator subgroup of a group G, the G/G′ is abelian.

Proof:

Let G′ x G′ y be two elements in G/G′

Then G′ xG′ y = G′ xy

Now (x^-1)^-1(y^-1)^-1x^-1y^-1= xyx^-1y^-1G′G

So G′ yx contains the elements xyx^-1y^-1yx = xy

But G′ xy contain xy: hence G′ xy = G′ yx

Theorem-3:

If N is a normal subgroup of G such that G/N is abelian then N ≥ G′

Proof:

Let N contain the normal subgroup generated by the commutators, if G/N is abelian, and x,y∈G, then

(xy)N = xNyN = (yx)N

Hence, xy = yx where n∈N

This implies that y^-1(xy) = y^-1(yxn), that is y^-1xy = xn,

And so x^-1y^-1xy = n ∈(x,y) = n∈N

⇒ N ≥ G′

That is, N contains every commutator.

Theorem-4:

If G is solvable and G∉E then G′ ⊂ G

Proof:

Let G be an abelian group and x,y∈G as x and y commute, then (x,y) = e and G′ the commutator subgroup of G generated by {e} then G′ ⊂ G

Theorem-5:

It G is simple, then either G′ = G or G′ = E

Proof:

Since G is a simple group, then it has only trivial normal subgroups, that is, if G′ is a commutator subgroup of G.

Then G′ = G

If G′ G′G then the only possible is G′ =E

Note:

Let G be a finite group. Let G′ be the commutator subgroup of G. We may form the commutator subgroup of G′ which we denote by G⁽ⁿ⁾ and so on, obtaining a sting of subgroups satisfying 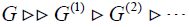where G′ = G⁽¹⁾ . This sting will terminate since G is finite.

If G⁽ⁿ⁾= E then we have solvable series for such group G. That means that G is solvable.

Theorem-6:

Let G be a finite group then G is solvable if and only if G⁽ⁿ⁾ = E for some integer n.

Proof:

If G⁽ⁿ⁾ = E, for some n, then G is solvable by the above note.

Now, assume that G is solvable and let N = {N₀,N₁,……..N_r} = E, with N_i ≠ N_j for i ≠ j, be a normal series of G with abelian factors. Then G/N is abelian and hence N ⊇ G⁽¹⁾ by theorems 2 and 3.

Since G⁽¹⁾ is a subgroup of a solvable group then G⁽¹⁾ is solvable and G⁽¹⁾ is a proper subgroup of G (unless G = E), G⁽¹⁾ = E , and so on.

Since G is finite, then the string of subgroups must terminate, that is G⁽ⁿ⁾ = E for some integer n.

Theorem-7: Let G be a group, Let H, K, L be subgroups of G, then

(i) (H,K) is a normal subgroup of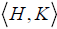

(ii) (H, K) = (K, H)

(iii) H normalizes K if and only if (H, K) ⊆ K

(iv) If K ⊆ H and both are normal in G, then

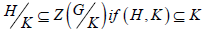
(v) If H, K, L are normal in G, then (HK, L) = (H, L)(K, L)

(vi) If ϕ in an endomorphism of G, then (H, K)ϕ = (Hϕ, Kϕ), and in particular (H, K) is normal in G if both H and K are normal [1-4].

Proof:

We shall show that for each x in (H, K) both xh and xk are in (H, K) for each h ∈ H and k ∈ K. Since x is a product of commutators, it will suffice to prove that both (y,z)^h and (y,z)^k are in (H,K) for each y, h ∈ H, z, k ∈ K.

But by property-2, (see 1.3) we have (y,z)^h = (y^h,z) (h,z)^-1∈ (H,K), while by property-3 (see1.3), we have (y,z)k=(y,k)^-1(y,zk) ∈ (H,K).

Thus 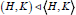that is, (i) holds. Now, by propery^-1, (see 1.3),(h,k) = (k,h)- 1. Since (K,H) is a subgroup, it follows from this that (h,k) ∈ (K,H) for all (H,K) ⊆ (k,H).Whence (H,K) ⊆ (K,H) by summary,(K,H)=(H,K) Hence, (H,K)=(K,H),that is,(ii) holds. Next H normalizes K if and only if h-1 k- h ∈ K for all h ∈ H, k ∈ K. Since, this equality holds if (H,K) ⊆ K then (iii) holds. Again, 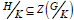if (Kh,Kx)=K for each h ∈ K, x ∈ G and (iv) holds. Now, case (v) follows easily from the property-2 (see 1.3) namely,(xy,z) = (x,z)^y (y,z) = y^-1 (x,z) y (y,z). Finally, the first assertion of (vi) is an immediate consequence of the relation (h,k)ȹ =(h ȹ,k ȹ) which holds for all h ∈ H, k ∈ K. If we take φ to be the inner automorphism induced by the element x of G, then second statement of (vi) follows also as a corollary.

Theorem-8: Let G be a group. Let H, K, L be subsets of G. If (H,K,L)=e and (K,L,H)=e then also (L,H,K)=e.

Proof:

Let us suppose that (H,K,L)= (K,L,H)=e. Thus, for all (x,y^-1,z)=(y,z^-1,x)=e, we have (x,y^-1,z) = (y,z^-1,x) =e. Hence, by property-4 (see 1.3), We have, (x,y^-1,z)=(y,z- 1,x)=e. But (L,H,K) is generated by the set of all such commutators (L,H,K)=e hence (L,H,K)=e.

Theorem-9: If X,Y,Z are subgroups of a group G, and if K is a normal subgroup of G containing (Z,X,Y)and (Z,X,Y) , then K also contains (X,Y,Z).

Proof:

This theorem follows from the property-6 (see1.3) where x ∈ X, y ∈ Y, z ∈ Z. That means 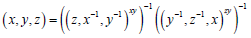gives the proof of the theorem.

Conclusion

Commutator properties and relative theorems are one of the promising and vital parts of group theory. According to my knowledge, not so much work has been done on it. Here, I have presented the theoretical aspects of Commutators. However, Commutators with respect to solvable groups might be applied to other directional research on both pure and functional mathematical computation such as in counting symmetries [12], field extension [13] and even to solve fuzzy problems [14-16]. If we run more research on it, then it might be able to contribute on the advancement of modern science and technology.

REFERENCES

1. Martin Isaacs I, Characters of Solvable Groups, American Mathematical Society (AMS). 2018;1-368.
2. Chekhlov AR, On Abelian Groups with Commutative Commutators of Endomorphisms. Journal of Mathematical Sciences. 2018;230:502–506.
3. Shahriar Shahriar, Algebra in Action: A Course in Groups, Rings, and Fields, American Mathematical Society (AMS). 2017;1-675.
4. Climenhaga V, Katok A. From Groups to Geometry and Back, American Mathematical Society (AMS). 2017;1-420.
5. Nasseef MT. A Study of Solvable Groups.LAP LAMBERT Academic Publishing, Saarbrücken, Germany. 2O13:1-64.
6. Grillet PA, Abstract Algebra, Springer Science & Business Media. 2007;1-674.
7. Abels H, Finite Presentability of S-Arithmetic Groups. Compact Presentability of Solvable Groups, Springer. 2006;1-182.
8. Paley H, Weichsel PM. A first Course in Abstract. Algebra Holt, Rinehant and Wimton, Inc. New York. 1966.
9. Hall M, jr, The theory of Groups, The Macmillan Company, New York .1955.
10. Herstein IN, Topics in Algebra XEROX College Publishing, Toronts. 1964.
11. Gorenstein D. Finite Groups, Harper and Row, Publishers, New York. 1968.
12. Nasseef MT. “Counting Symmetries with Burnside’s Lemma and Polya’s Theorem, European journal of pure and applied mathematics. 2016;9:84-113.
13. Nasseef MT. Field Extension by Galois Theory, General Letters in Mathematics. 2017;3:132-153.
14. Arqub OA, AL-Smadi M, Momani S, et al. Numerical solutions of fuzzy differential equations using reproducing kernel Hilbert space method, Soft Computing. 2016;20:3283-3302.
15. Omar Abu Arqub, Mohammed AL-Smadi, Shaher Momani & Tasawar Hayat, Application of reproducing kernel algorithm for solving second-order, two-point fuzzy boundary value problems, Soft Computing 2017;21: 7191-7206.
16. Arqub OA, AL-Smadi M, Momani S, et al. Adaptation of reproducing kernel algorithm for solving fuzzy Fredholm-Volterra integrodifferential equations, Neural Computing & Applications. 2017;281591-1610.