Einstein metrics and two projection maps

Received: 04-Sep-2018 Accepted Date: Sep 06, 2018; Published: 01-Oct-2018

Citation: Kalmbach GHE. Einstein metrics and two projection maps. J Mod Appl Phys. 2018;2(2):19-22.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

The Minkowski metrics relativistic factor and the Schwarzschild metric rescaling factor for the affine Minkowski metric are set in octonian coordinates 0,1,...,7 to a stereographic projection using a projective homogeneous norming and to a nonlinear rescaling of a gravitational compass needle from a barycenter B to a system Q in spiralic rotational motion with an orthogonal projection. The two projection geometries for this can come in both versions using for the rescaling. Most statements of this kind are in this article my contribution coming from nuclear geometry considerations. It stresses the geometrical nuclear reasons for the existence of the two metrics. Einstein makes for gravity GR a curved Riemannian metric computation from which I don’t compute newly for instance the Schwarzschild radius Rs of a mass system in the universe. In mathematics his metric is proved by analysis and an energy momentum tensor computation. It is not coming from an octonian geometry for particles as described here.

Keywords

Moebius transformations; Minkowski metrics relativistic factor; Schwarzschild metric rescaling factor; Stereographic projection; Nucleons; Theorem of Pythagoras

Introduction

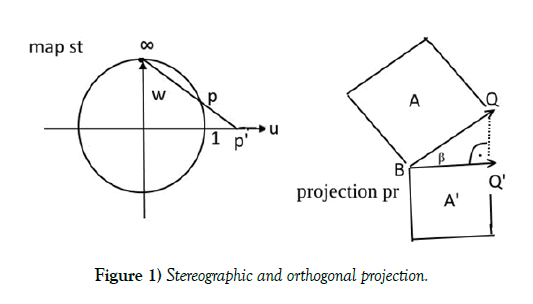
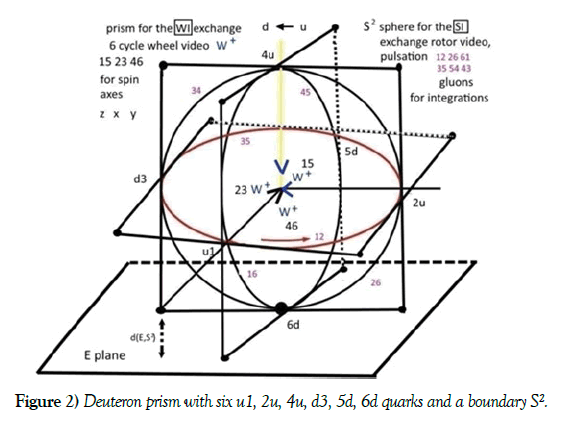
Discovering recently the time-space rippling of graviton waves means in my particle oriented research that rgb-graviton whirls, belonging to first three strong interactions SI Gell-Mann matrices project the complex 3-dimensional SI space 12...6 onto the 4-dimensional spacetime. The two projection geometries for this can come in both versions using for the rescaling Figure 1. The Einstein 4-dimensional model 1234 is dimensional extended (6 down to 4) has also done in TV (3 down to 2 dimensions). Projective homogeneous, not only Einstein’s affine geometry applies. The spacetime rippling is in the nuclear range through a stereographic projection in Figure 2 from a complex 1-dimensional Riemannian sphere S² (prism) on an E plane since this GR action is in another 2356 octonian SI subspace and the flat E is in the Eucliden spacetime 1234 (time is the octonian coordinate 4). The observed nonlinear rippling of space coordinate units is in Figure 2 the change of the distance from S² to E (stretching or) contracting length/ radius differentials like dr’=dr/cosβ, sin²β=Rs/r, r radius (for time t it is dt’=dt·cosβ).

Figure 1) Stereographic and orthogonal projection.

Figure 2) Deuteron prism with six u1, 2u, 4u, d3, 5d, 6d quarks and a boundary S².

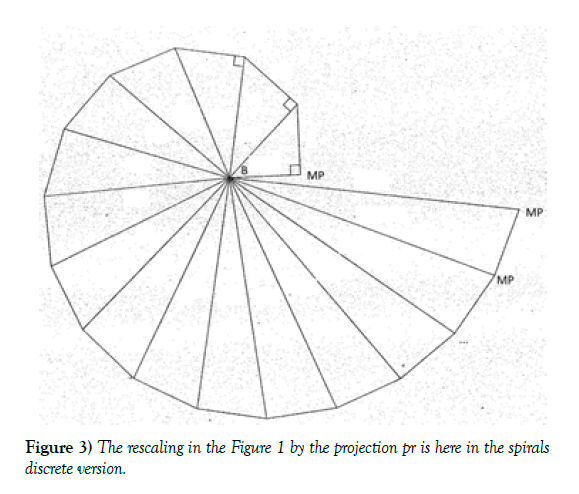
The construction of nuclear barycenters B occcurs in my model through a strong interactions time crystal dynamics for nucleons and atomic kernels. It uses the Schwarzschild radius inverted gravitational potential to a matter bounding ball radius of a S² with an inner volume related to the second cosmic escape speed. The projective normed Schwarzschild factor arises from an asymmetric distance measure |BQ|=r, |QB|=r-Rs, Q an orbiting mass system in GR interaction with some central B. The area of the square A above the coordinate needle vec(BQ) is reduced in an orthogonal, spiralic projection pr (Figure 3) to an area A’ of the projected needles vec(BQ’) length squared according to the theorem of Pythagoras. Such a flat change of orbit is also observed for Kepler’s conic sections where a planet Q rotating about a central sun with barycenter B gets from the accelerating rgb-graviton whirls action after one rotation an additional angle added for its rosette orbit [1]. The P orbit is not falling into a curved potential GR pot of the sun. rgb-graviton whirls are experimentally found in my opinion as neutral color charge of nucleons.

Figure 3) The rescaling in the Figure 1 by the projection pr is here in the spirals discrete version.

The map st

The stereographic map st rescales along a ray R from a point at infinity ∞εS¹ the length |∞P|, P=(u, w)εS¹, at perpendicular height line w to the length of its projection |∞P’|, P’=st (P)εR at height 0 on the horizontal projection line as u-axis for S¹-{∞} in a uw-coordinate plane. The inverted speed from dark energy at speed of light c to a group speed v<c of matter generates the st rescaling. In the homogeneous projective ray norming of st, [|∞P|, 0, (1-w)=cos φ] is mapped to [|∞P|/cosφ, 0, 1] where β = φ can be taken in the projection pr figure. The same rescaling is for P on the lower half of the circle and its ray hitting u = 0 line in P’. As relative speed v of the affine Minkowski metric the value is sin φ=v/c. Geometrical invariants are proportions and parallelity of lines. The ray norming uses the 3×3 matrix for a coordinate unit m=|∞P| with coordinates a11=1=a32, a33=-1 and 0 otherwise, projecting the ∞P [m, 1, w] and BQ vectors into [m, 0, (1-w)] and BQ’. This belongs to the system whose m value is measured in the apparatus system special relativistic [2] scaled up or down projected: length as l’=l·cos φ. time t’=t/cos φ, mass m’=m/cos φ and a lights transversal Doppler effect for the systems frequency f when the apparatus (moving transversal to the ray) measured frequency is f’=f·cos φ.

This octonian setting is from my research in [3], the lights symmetry U(1) st central projection adds the special relativistic scaling factor cos φ.The 7th octonian coordinate is for lights symmetry U(1) rolled to the Figure 1 circle S¹. This is linearly stereographic projected to the octonian coordinate 7 as u-line adding the cos φ scalar above. For generating the speed v itself, in [3] the rescaling of the u-quark mass in a nucleons mass weight is attributed to a relative speed v between two coordinate systems, its barycentrical weight as sum of three quarks masses measured in strong SI barycentrical coordinates and the single u-quark mass measured in weak interaction WI Euclidean coordinates. The relative speed is here for generating a common optical group sped as v=∂ω/∂k of the system through a special relativistic mass rescaling. Gleason measure operators [4] are used in [3] for this. They are generated by pairwise orthogonal coordinate triples like those of spin space coordinate units, but having as vector weights for instance the three nucleons u-, d-quark masses.

The prism explanation is too long and is found in [5]. The hedgehog sphere S² in Figure 2, bounding a deuteron atomic kernel [5], is carrying as rgb-graviton through color charge vector GF triple on octonian 1, 2, 3 coordinates with the three quark masses attached. In the strong toroidal, fibre bundle geometry S³×S5 [6] the hedgehog sphere is the boundary of the homogeneous projective norming of S5 [7] to an inner deuteron space 2356 as projective complex 2-dimensional space CP² [8].

The spiralic orthogonal projection map pr

In the first section, the coordinate units of a system E at rest are rescaled in a measuring apparatus in Minkowski motion against E. For two systems Q, P in gravitational GR interaction, its affine Minkowski metric for spacetime coordinates ds²=dr²-c²dt² has to be GR (Schwarzschild) rescaled.

As in the abstract, Q, P can be mass systems where P (planet) is on a rotational orbit about a central Q=B system (sun) and has as GR needle length |QP|=|BQ|. In the nuclear case treated in [3], B can just be a barycenter, not an additional mass system. The Schwarzschild radius Rs mass belongs to Q. As mentioned above and in [3], the unsymmetric distance measure between P, Q occurs through the vec(QP) |QP|=r length and the vec(PQ) |PQ|=r-Rs length where P can measure its distance towards Q only up to the Schwarzschild radius of Q. In homogeneous octonian coordinates the two measuring coordinates are […, r-Rs,...,r,...] and the homogeneous norming with the Schwarzschild factor cos²β, sin²β=Rs/r as central projection is with […,(r-Rs)/r,...,1,...].

The metrical coordinate units dr, dt of ds²=dr²-c²dt² are homogeneously rescaled by dr’=dr/cos β, dt’=dt·cosβ for the GR interaction Schwarzschild metric ds’=dr²/cos²ÃŽÂ‡β-c²dt²ÃŽÂ‡cos²β. The orthogonal spiralic contraction/ expansion of the needles length is due to a rgb-graviton whirl GR action. Further descriptions are found below or in [3].

Rgb-gravitons: Moebius transformations and Gleason measures for the prism

Beside the gravitons wave character, found in experiments, they have in the prism through a color charge presentation as superposition of three color charge whirls r, g, b as rgb-graviton a deuteron quarks triangle Δ radius contraction/expansion. Mathematically, whirls are computed through div, rot dual to waves, hence there are three energy characters, particles, waves, whirls, extending the physics wave-particle through considerations from mathematics. From the Gell-Mann matrices the first three λ1, λ2, λ3 projections present the three rgb-graviton. They project the deuteron prism S² in Figure 2 as Hopf spere S²=h(S³) down to the plane E below where their action can change through the GR potential and whirl the distance d(E, S²) for length contraction or expansion of the projected images [9] with the rescaling Moebius transformation MT b-id, b a real constant. The relation of the three b values for d(E, S²) is measured through the G (an MT of order 6) rotation angles of 30, 60, 90 degrees. For half of the G turning angle b=1/2 (fermion spin) for the G turning angle b=1 (boson spin). Then the π/2 angle is used for changing the G presentation through cos²β into the second cosmic speed (squared) sin²β by using cos(β+ π/2)=-sin β. The relation between the (squared) first to the second cosmic speed is set with b=2 for the rgb-graviton spin. This b proportion 1:2 comes from the conic precession motion PM of the SI rotors cone Cn about a barycentrical coordinate axis of the nucleon triangle where its Cn turn for the rotation is with spin 0 for its momentum. This gives for a nucleon the Landé factor g=1. For electrons Hopf S² spin (cone Cs) the rotation is with angular momentum 0 and an electrons/positrons Landé factor g=2. For the PM conic rotation of the two rotations Cn, Cs the angular momentum L=Jω has the length |L|=a·g for a constant J; the Larmor frequency for the motion in an outer magnetic field B is ω=-gB·e0/2m (for a electron/positrons or nucleon) is scaled by g where μi=(e0·h)/(4π·m) is the kernel or Bohr magneton used in the gyromagnetic relation [10] as γ=g·e0/2m=2π·gμi/h, the coupling of spin s with magnetic momentum μ in |s|=γ·|μ|.

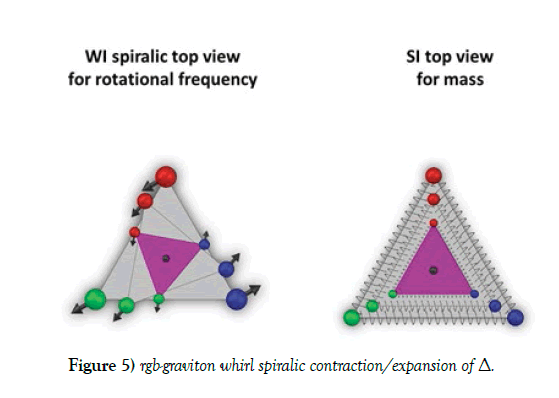
In a spin lengths normed way, the nucleon triangle is rotated and spiralic radius rescaled in WI coordinates in the right part of Figure 5 and in the left part in SI coordinates barycentrical rescaled, the three basic spin length orbit of the triangle symmetry as ½, 1, 2 measures the outer triangles (normed) side of Δ1 as the graviton spin 2. After the first 30 degree orthogonal projected turn, the triangles Δ2 side length is only the half side length 1 for gluons/bosons spin; this is repeated for fermion/quark spin length ½ in the third projection to Δ3. The plane for the rescaling is different from the stereographic st version in Figure 1. It has as generating coordinates the radius as distance measure and in polar plane coordinates r·exp(iβ) the needles rescaling through projection on the x=r·cosβ line (or upwards). The pendulum motion of this geometry is due to the symmetry of the normed MT G coefficient matrix of the Schwarzschild factor. The cyclic G group of order 6 is isomorphic to the group {id, α, α²} of the triangle rotation group with the conjugation group {id, C} in which conjugation commutes with α. Conjugation as G³=-id reverses the pendulum motion length ½ from contraction to expansion. G makes the first contraction from length 2 to length 1, G² the second contraction from 1 to ½, G⁴ the first expansion from length ½ to length 1 and G5 the second expansion from length 1 to length 2 and G⁶=id (identity) reverses the expansion to contraction. The quantized energy allows together with the G symmetry group the three spin lengths bounds for the quark triangles pendulum motion. Spin ½ is the smallest (E=hf energy) grid value for the nucleons (fermions, quarks) area where conjugation G³ reverses the orientation of the pendulum motion. Otherwise the quarks SI rotor decays into other energies, they cannot have a smaller than Planck size spin length. At this pr projection the GR force is integrated in the SI rotors time cycle of [3] to v1², the squared first cosmic speed E(pot). This adds up as GR interaction in astronomy to the free fall threshold for small mass systems P falling down to a central huge mass system Q. Inner entropy E(heat) of deuteron is integrated in the SI rotors time cycle inside its volume. The heat flow through the quark triangle is measured after the G⁴ action as nucleons inner entropy. The second cosmic speed v2 as the G Schwarzschild factor in v2²/c²=Rs/r is this threshold for escape of P from Q in astronomy. Another reason for this threshold in the prism Figure 2 is from the SI force strength in a nucleon. The boson/gluon spin value 1 ford(E, S²) is from the strong interaction gluon exchange (boson) between confined quarks. It is known that adding energy for drawing two quarks in a meson apart is stored until from the inner energy a weak boson can be generated and this decays into two mesons. The SI force allows no gluon exchange between quarks for larger distances of d(E, S²). This kind of decay process is similarly present in the nuclear atomic kernels AK decays where the weak force as isospin exchange between the neutron-proton pairs as Cooper pair is not possible for larger distances in an AK.

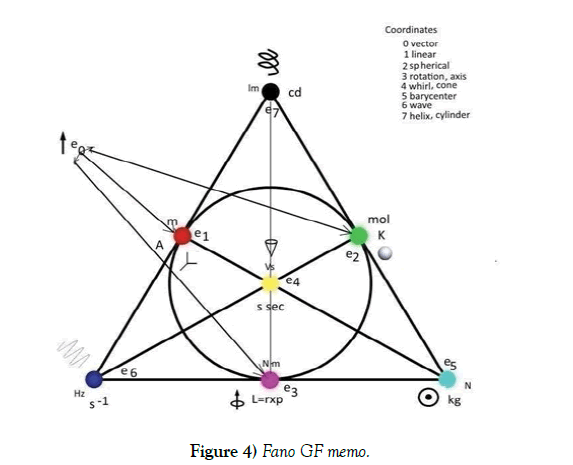
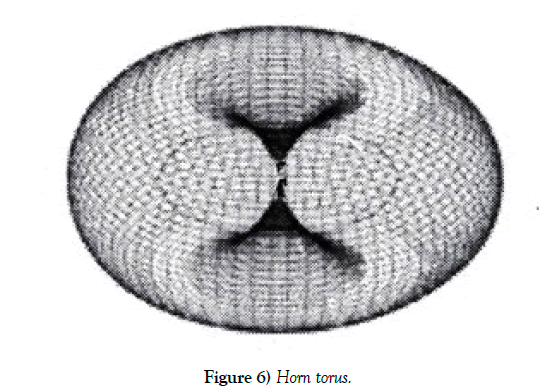
For other integrations in the SI rotors time cycle is mentioned that after the G² contraction spins together with magnetic momentum (the gyromagnetic relation holds) of quarks are gyromagnetic arranged (anti-)parallel for energy savings to a common nucleon spin with magnetic momentum vector. In addition the magnetic field flow through the quark triangle is measured [5]. Generated is the magnetic induction known as Gleason frame (real cross product [11]) GF triple (the Fano memo line 145 in Figure 4) where the electrical charge +1 rotates on the circumference S¹ of the proton triangle as in an electrical current. The GF triple (the Fano memo line 246 in Figure 4 for the energy E(heat) flow integration), the G⁶=id length scaling action action above is [volume times pressure equals heat], S¹ as volumes boundary, pressure replacing induction in 145. For the G³ action above with the first cosmic speed threshold the GF triple (the Fano memo line 257 in Figure 4) is E(pot) as rgb-graviton color charge whirls flow through the nucleon triangle where mass as point charge is rotating on S¹, adding an GR induction. For angular energy E(rot) (the Fano memo line 347 in Figure 4, the G⁴ action) the GF triple is L=rxp, L the angular momentum, p momentum, r radius; S¹ is an r-orbit of the rotating system and its momentum p=mv vector rotates on S¹ as tangent vector, L is an induction. The momentum E(kin) energy (the Fano memo line 356 in Figure 4, the G⁵ action) has as GF triple p=mv with the E(rot) (v as ω=rv angular speed), E(kin) (as p SI rotor vector attached to S¹), E(pot) (as m point rotation on S¹) vector triple for the nucleons SI time crystal cycle; barycentrical coordinates are generated through the triangle symmetry D3 presentation. The electrical potential EM(pot) (the Fano memo line 123 in Figure 4, the G action) is for the isospin weak WI cycle; Euclidean coordinates are generated through the σj Pauli spin matrices SU(2) presentation as GF triple σ1, σ2, σ3; EM(pot) is an electrical charge point e rotating on S¹, the rotation axis carries in the generated Hopf S² presentation on its north pole N spin s plus magnetic momentum μ. The + or - orientation of the e rotation changes the orientation of μ towards s and the tangent speed vector to S¹ at e is momentum p. In the case of neutral leptons ν s is (anti-)parallel top on the S² south pole as helicity, using a geometrical spindle torus Hopf presentation for ν, its rotating point charge is neutral in two + or - orientations. The geometrical S³ sphere of the weak WI SU(2) geometry is projected down to S² [12]. For the rgb-graviton whirl presentation (Figure 5) through the λ1, λ2, λ3 matrices replacing a GF triple, the Pauli matrices are extended to these projection maps; the geometrical S5 factor of the SI SU(3) geometry S³×S5 as complex (z1, z2, z3) SI space with a z3 complex energy 56 plane for mc²=E=hf is projected down to spacetime coordinates 1234 z1=z+ict, z2=x+iy as complex Hopf plane. The last Fano line 167 is for light with the U(1) circle S¹ symmetry. This octonian 7th coordinate is rolled to a Kaluza-Klein loop for cylindrical coordinates. The change from polar to linear complex coordinates is as usual. It introduces the periodic exponential exp(iφ) function for wave ψ presentations and cylindrical complex polar coordinates r·exp(iφ). The wave length λ is measured on the axis A of the cylinder as length of a helix line with one winding. Winding numbers are also for spin length quantizations. One helix winding carries the Planck quantized photon energy E=hf, measured as frequency f in λ·f=v as speed with the upper bound v=c for light in the universe; the energies helix line (replacing a rotating point charge) moves with its momentum p=hf·v/ c² along A. Here mass m is replaced by frequency, no G action occurs. As replacement the Minkowski relativistic scaled M=G·σ1 matrix acts. The light cone geometry is added. In projective coordinates, the Horn torus surface (Figure 6) is cut either at the Horn torus singular point at infinity to a cylinder or in a transversal plane deleting a transversal circle at infinity. In the former Gleason frame triples description the S¹ circle for U(1) is geometrical extended to the cylinder surface CS, the energy field flow through an S¹ area is replaced by the lights helix generated frequency as flow on CS with wave length λ. In the above cross product the EM induction is replaced by the speed of light c. In addition, the exponential ψ wave function representation for waves is generated using ω=rf as frequency. - These results are from [3].

Figure 4) Fano GF memo.

Figure 5) rgb-graviton whirl spiralic contraction/expansion of Δ.

Figure 6) Horn torus.

The left part of Figure 5 has an interpretation through 3 dogs at the triangles vertices perusing (or spiralic running away) from one another head to tail on a circle with constant speed.

Also for other geometries the line at infinity ×2 can be changed for getting suitable coordinate representations. For the Horn torus case one can transform homogenous coordinates as y²+z²=1 circle in [y, z, x2] to [x2, z, y] coordinates for a hyperbola presentation, change the coordinates to r=x2, ict=z and set y=0 for r²=c²t², the bounding cone surface of the 2-dimensional Minkowski cone. It is then 3-dimensional blown up to r²=x²+y²+z² in Euclidean Hopf space coordinates. If for light λ·f=c as constant speed is used and the Kaluza Klein loop is presented in a polar coordinates (r, φ) plane, λ is taken as the cylindrical A axis coordinate as line at infinity the linearized r-coordinate is chosen and normed to r=1 for S¹ then in [φ, λ , f, 1] coordinates the spin quantizing winding number n is presented though the matrix transformation with coordinates a11=1=a44, a22=n, a33=1/n, a14=2πn and aij=0 otherwise to [φ+2πn, nλ, f/n, 1], a periodic φ translation and a scaling for λ’s A axis energy expansion of the lights helix line. f is taken as inverse time interval where time Δt is discrete changing with n. A photon is one full winding of the helix line part and its energy is annihilated if no full helix winding occurs in the lights time expansion. The relativistic corrections for light are due to the Schwarzschild metric.

Concerning rgb-graviton whirls [13], the relation to mass as rotating charge on S¹ from above for the Gleason frame 257 can have as induction (cross product) the gravitational waves ψGR observed stretching and squeezing of spacetime through the Schwarzschild metric. The 257 integration was due to a rgb-graviton flow through a loop on which a mass charge (replacing an EM current) is rotating. For ψGR this is presented as in the case of light with the U(1) symmetry, ψGR has an angular frequency, the rotation is on a cylinder surface as one winding of an GR energy carrying helix line. In the light case the rgb-graviton whirls can be small photon cones like magnetic field quantums with the cylinders S¹ boundary whose rotating charge on S¹ as energy traces out in time as translation along cylinder axis the helix winding line. The geometry for the GF triples and the associated energy are different.

We mention as final remarks that for E(rot) the plane for the whirls upper S¹ circle is parallel to the axis A Euclidean shifted to the plane E through the tip of the cone for the E(rot) rotation about A and S¹ is replaced by the orbit (conic sections, rosette, ...) of a system rotating about A in E. For E(kin) the SI rotor [14], [15], [16] for the six roll mill) cones are in use. For heat it is like a normal phonon whirls (without a spin but a momentum and energy transfer) stochastic flow in time through areas of different shapes from warm to cold. For EM(pot) one can use the inverse Hopf map for the Hopf sphere S² where charged leptons have a fibre S¹ blown up EM charge rotating on a torus and the leaning spin plus magnetic momentum vector has a cone rotation about the central blown up torus axis. The WI Hopf S³ geometry for weak decays is not through the Pauli spin matrices GF triple. The decays split S³ according to the Heegard decompositions into two solid 3-dimensional balls, into two solid brezels [17] of genus 1 with a torus surface for charged leptons location where the torus can also be split along a transversal circle to the finite cylindrical locations of helix lines with one winding for waves and into two solid brezels of genus two for quarks location whose two electrical charge and mass poles of the central lemniscate brezels retract. For the leptonic torus case the Hopf blow up is for mass on the central circle of the contracted tori and the second leaning transversal circle fibre S¹ of the torus is for the electrical charge location. Its helix winding as frequency on the torus surface has to fit to a radius which generates the Bohr radii changes for the electrons shell location in an atom when the helix winding is not full, i.e. not closing as curve on the torus. For these two kinds leptonic torus and cylindrical light frequencies as spectral series the rescaling is using the Rydberg (fine structure) constant as known [2] from the computation of the leptons ψ function for matter waves. If such a rescaling for ψGR waves is wanted, the basic spin norming’s ½, 1, 2 for the prisms d(E, S²) norming as the (scaled) nucleon triangles three Bohr radii can replace the discrete quantum number n for spectral numbers ψ. The E(pot) GR rescaling from rgb-graviton whirls to ψGR waves is first to the cos²β factor as G matrix with half of the turning angle of G and spin 1/2 in the spiralic pr Figure 3 as threshold for free fall, then using the GR potential in sin²β/2 and spin 1 and the turning angle of G for rotating systems about a central system or barycenter, and for the third value of d(E, S²) the turning angle π/2 and the escape speed sin²β as threshold. The E(pot)+E(kin)= constant preservation theorem is used for rotations.

For the MT symmetry of S² we mention only inversions [9]: The speed v’ inversion from dark energy at c is by v’·v=c² where v<c is the speed of quark matter systems in the universe and light with speed c is at this bounding circle as normed U(1). This is replaced for the GR interacting systems by the scaled potential to radius inversion at the Schwarzschild radius in (1/r)·r=Rs² for high mass inside an accregation disk of a black hole (dark matter) and small (quark) masses inside the deuteron or nucleons or matter of radius r>Rs. Both inversions are from [3].

REFERENCES

1. Stephani H. General Theory of Relativity. German publishing house of the sciences, Berlin. 1991.
2. Sexl RU, Urbantke HK. Relativity, Groups, Particles. Springer. 1992.
3. Kalmbach GHE. MINT-WIGRIS, MINT Verlag, Bad Woerishofen. Scholars' Press, Beau Bassin. 2017.
4. Dvurcenskij A. Gleason's'Theorem and its Applications. Kluwer Acad Publ. 1993.
5. Kalmbach GHE. Deuteron States. J Phys. 2017;1:1-17.
6. Kalmbach GHE. Hedgehog balls for nucleons. PJAAM. 2013;7:1-5.
7. Schmutzer E. Projective Uniform Field Theory with Applications in Cosmology and Astrophysics. 2004. (The unified electrical and gravity fields is here 5-dimensional with three 4-dimensional projections similar to the above octonians in [1] into spacetime (e1, e2, e3, e4), the deuteron space (e2, e3, e5, e6) and a scalar field (e1, e4, e5, e6).
8. Kalmbach GHE. Quantum Measures and Spaces. ISBN 0-7923-5288-2.
9. YouTube: Moebius Transformations revealed. 2014.
10. Physics of matter. K Bull City, VCH, Weinheim-New York, Basel, Cambridge. 1989.
11. Cross products and Gleason frames. PJAAM. 2014;10:1-15.
12. Kalmbach GHE. (Chef-Hrsg.), MINT (Mathematik, Informatik, Naturwissenschaften, Technik), MINT Verlag, Bad Woerishofen. 1997;pp:1-36.
13. Hellwig KE.  A Graviton Group D3. Quantum Structures. 1996.
14. Byrd M. The geometry of SU(3). physics/9708015. 1997;1-17.
15. Poston T, Stewart I. Catastrophe theory and its applications. Pitman (the 6-roll mill for deuteron integrations), London. 1978;p:3.
16. Berry MV. The six-roll mill and The elliptic umbilic difraction catastrophe. Phil Trans Roy Soc A. 1980;pp:453-84.
17. Langer JC. On meromorphic parameterizations of real algebraic curves. J Geom. 2011;pp:105-28.