Fluids flow stability in ducts of arbitrary cross-section
Received: 18-May-2018 Accepted Date: May 28, 2018; Published: 04-Jun-2018
Citation: Delplace F. Fluids flow stability in ducts of arbitrary cross-section. J Mod Appl Phys. 2018;2(2):10-15.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
Fluids flow stability is of major importance in both research and engineering. Transition between the laminar and turbulent flow regimes is often characterized by critical Reynolds number value. In this paper, we used experimental results obtained in ducts of several cross-section shape, to analyse the deep link between geometry and flow stability. Experiments clearly showed the influence of geometry on critical Reynolds number values. Considering isoperimetric quotient (IQ), coming from famous isoperimetric theorem, we established and quantified the link between fluids flow stability and IQ. Moreover, we showed that an abacus could be built giving critical Reynolds number values as a function of cross-sections IQ. This abacus could be an interesting and important tool for both research and engineering applications.
Keywords
Flow stability; Critical reynolds; Friction curve; Ducts cross-section; Isoperimetric theorem; Curvature
Introduction
In fluid dynamics, hydrodynamic stability aims to find out if a given flow is stable or unstable, and if so, how these instabilities will cause the development of turbulence [1]. The Reynolds number is the most important tool used in both research and engineering, to determine the flow stability and then the flow regime in a pipe. In a very complete paper [2] gave a review of mechanisms and possible explanations for phenomena involved during the transition between laminar and turbulent flow regimes. The role of disturbances was of course discussed as a major source of flow instability. In this paper, we will only consider the case of “normal” disturbances; i.e. disturbances encountered in classical pilot-plants experiments or in industrial devices. These conditions give a critical Reynolds number around 2000 for a pipe of circular cross-section shape; even if this value can reach 100,000 by minimizing all ambient disturbances [2].
Flow regime has a considerable importance in transport phenomena, and then for industrial applications involving heat, momentum and mass transfers. Most of the time, experimental and numerical studies are carried out in tubular geometries but development of high performances heat exchangers and nanotechnologies requires more and more accurate knowledge of fluids flow in arbitrary shape pipes and ducts. Recent paper of Manish et al. [3] well illustrated this need for a better understanding of flows in complex shape geometries.
Laminar flow in ducts of non-circular cross-section was widely studied, and famous theoretical work of Shah et al. [4] is undoubtedly the best reference. Poisson’s partial differential equation can be solved analytically or numerically depending on the cross-section shape geometry giving the boundary conditions (Dirichlet problem). Results are of course the velocity fields for the different geometries. But in the transition and turbulent flow regimes, the study of the flow in ducts of complex cross-section is much more complicated and there exists a relatively small amount of experimental and numerical results due to the complexity of Navier-Stokes equation which remains unsolved. But, due to the huge interest around this very complex mathematical problem, recent publications gave both analytical and numerical results of major importance [5-9].
A concrete example of complex geometry is plate heat exchangers (PHE) which are widely used in the industry. It surely explains why, their very complex flow passages hydrodynamics, was experimentally studied by many authors [10-12]. PHE friction curves gave a better understanding of liquids flow in complex shape flow passages; even in the case of non-Newtonian liquids encountered in food processes. As clearly reported by Delplace [12], these results showed a very low value of critical Reynolds number (Rec) compared to well known values found for pipes. For a single PHE channel, 10 ≤ Rec ≤ 30 and Rec ≤ 10 for a complex PHE flow arrangement [11]. All PHE experimental results showed that the complete friction curve, spanning all flow regimes, does not exhibit a marked transition region like in pipes. As a consequence, a simple Ergun type model allowed all flow regimes to be described. Finally, Delplace [12,13] compared experimental friction curves in a PHE channel and in several ducts having triangular, square, rectangular and circular cross-sections. These results were obtained with a huge number of experimental data and several liquids, both Newtonian and non-Newtonian and they are a strong source of information. They clearly showed the influence of geometry on flow stability and the huge difference of friction factor values between PHE and regular pipes.
Turning now on recent theoretical developments in fluid mechanics and geometry, Delplace [14] showed that Reynolds number can be considered as the ratio of two curvatures: pipes cross-section curvature defined through hydraulic radius and flow velocity field curvature due to inertia and fluid dynamic viscosity. Moreover, in an applied Mathematics paper, Delplace [15] demonstrated that hydraulic radius based curvature can be extended to n-dimensional shapes and then can be used for 3D flows. These approaches suggest that shapes curvature, considered as a major parameter in Physics [16], could be useful for the study of hydrodynamic stability and then for turbulence apparition in ducts of arbitrary cross-section shape.
In the first part of the present paper, we will detail above results and give the main relationships used for experimental friction curves description and critical Reynolds number values determination. In a second chapter, we will analyse results using both Poiseuille number (Po: product of friction factor and Reynolds number in the laminar flow regime) and cross-sections curvature in order to predict critical Reynolds number values. Finally, we will conclude by giving a possible explanation of the influence of cross-sections geometries on the transition between the laminar and turbulent flow regimes. This result, based on one of the most famous theorem in geometry, gives for the first time, a clear and simple mean to determine fluids flow stability in ducts and then to improve geometries used in industrial applications.
Experimental Friction Curves in Ducts of Complex Cross-Section Shape
Using a large number of Newtonian and non-Newtonian liquids, Delplace’s experiments [12,13] consisted in pressure drop ΔP(Pa) and flow-rate measurements, in regular ducts having circular, triangular, square, rectangular and elliptical cross-section and in a PHE channel. For Newtonian liquids (water and dilute sucrose solutions), this author calculated classical dimensionless numbers i.e. the Fanning friction factor f /2 and the Reynolds number Re defined as followed:
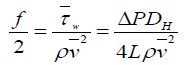 (2.1)
(2.1)
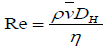 (2.2)
(2.2)
In these equations, 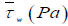 is the average wall shear stress along the cross-section perimeter;
is the average wall shear stress along the cross-section perimeter; 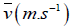 is the liquid mean velocity;
is the liquid mean velocity;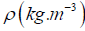 its density; L(m) is the pipe length where pressure drop ΔP(Pa) is measured; DH(m) is the hydraulic diameter and η (Pa.s) is the liquid dynamic viscosity. As reported in Delplace [12] liquids physical properties
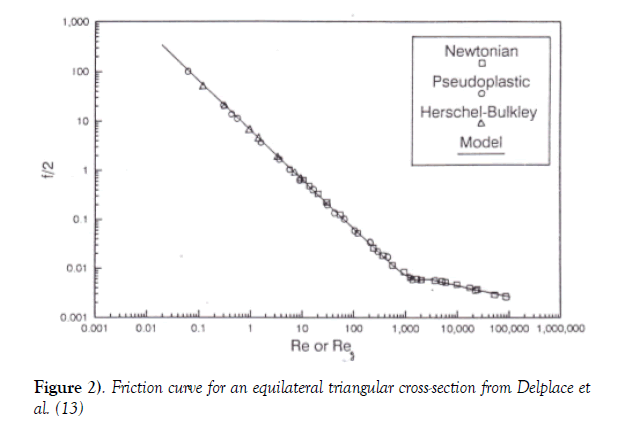
its density; L(m) is the pipe length where pressure drop ΔP(Pa) is measured; DH(m) is the hydraulic diameter and η (Pa.s) is the liquid dynamic viscosity. As reported in Delplace [12] liquids physical properties 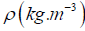 and η ( pa.s) were measured in the laboratory by use of a densimeter and viscometers. Of course, temperature variations were carefully taken into account in the calculation of these physical properties. The following Figures 1 and 2 taken from Delplace et al. [13] illustrate excellent correlations obtained, for a wide range of Reynolds number values (from 10-1 to 105), and a wide range of viscous behaviours.
and η ( pa.s) were measured in the laboratory by use of a densimeter and viscometers. Of course, temperature variations were carefully taken into account in the calculation of these physical properties. The following Figures 1 and 2 taken from Delplace et al. [13] illustrate excellent correlations obtained, for a wide range of Reynolds number values (from 10-1 to 105), and a wide range of viscous behaviours.
Figure 1) Friction curve for square cross-section from Delplace et al. [13]
Figure 2) Friction curve for an equilateral triangular cross-section from Delplace et al. [13]
As reported above, these experiments covered all flow regimes. For laminar flow, the slope of friction curves is (-1) and Poiseuille number: Po = f /2.Re , values were in perfect agreement with theoretical values reported in Shah et al. [4] i.e. 7.11 for a square duct, and 6.67 for an equilateral triangular duct. For transition flow, the friction curve slope clearly changed, until it reaches the fully developed turbulent flow regime, and the final slope. These results were comparable to those obtained in smooth tubes of circular cross section.
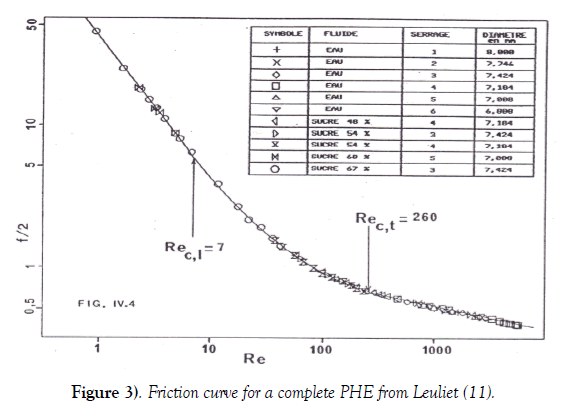
For PHE channels, friction curves were quite different; especially in the case studied by Leuliet [11] of a complete PHE configuration. The following Figure 3, clearly illustrates both the difference in friction curve shape and friction factor values.
Friction factor values were clearly larger than previous ones and the value of critical Reynolds number was very low: Rec = 7. Being aware of the Leuliet’s [11] PHE complex flow configuration, Delplace and Leuliet, working in the same laboratory, decided to study a single PHE channel in order to eliminate singularities due to brutal changes in flow direction in the complex flow arrangement. Delplace [12], using a large amount of liquids, both Newtonian and non-Newtonian, obtained the following friction curve for the single channel.
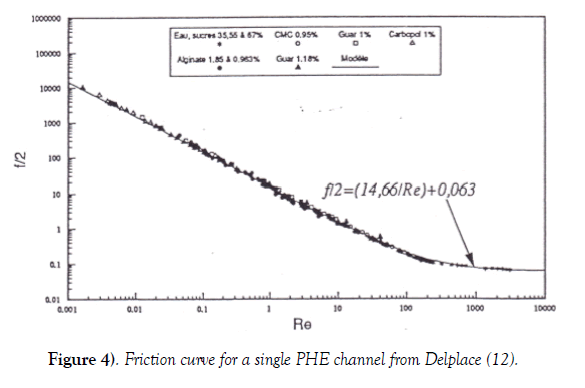
The shape of the curve remained the same but critical Reynolds number value clearly increased: Rec = 30 and Poiseuille number value largely decreased from 40.6 [11] to 14.66 as reported in Figure 4. This last value was more in agreement with values reported in source books [10] confirming the role of changes in flow direction in the case of Leuliet study [11]. These results will be discussed and interpreted in the second chapter of this paper.
Figure 3) Friction curve for a complete PHE from Leuliet [11].
Figure 4) Friction curve for a single PHE channel from Delplace [12].
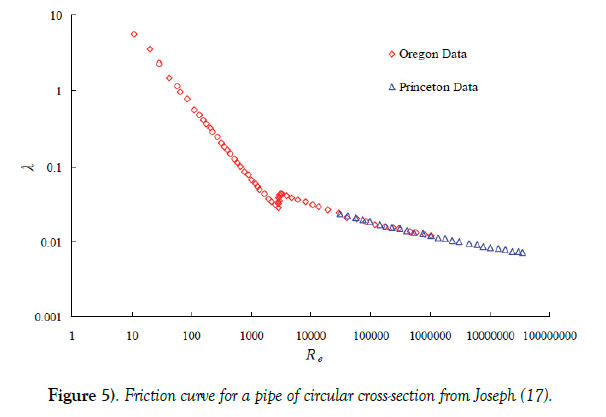
As reported by Joseph [17], modelling of friction curves is very important. As showed in above examples, determination of critical Reynolds number Rec values is not easy, and it requires a large amount of measurements around the transition region; in order to determine when the slope of friction curve changes from (-1) which is the characteristic of laminar flow.
The following friction curve for a smooth pipe of circular ross-section was taken from Joseph [17] and it shows that even for the most common geometry (circular cross-section), a large amount of data, covering a large range of Reynolds number values is necessary to accurately determine for that well-known case (Figure 5).
Figure 5) Friction curve for a pipe of circular cross-section from Joseph [17].
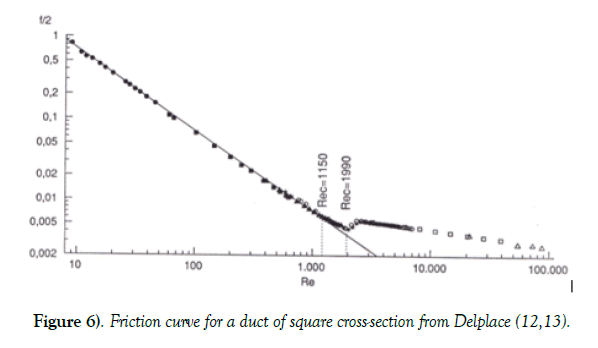
Delplace [12,13] applied the same approach for all geometries tested. For example, the following friction curve was obtained for the duct of square cross-section allowing a critical Reynolds number value Rec=1150 to be accurately determined (Figure 6).
Delplace [12,13] used the powerful modelling method proposed by Churchill [18] for friction curves obtained in his geometries reported above. The main advantage of Churchill’s [18] approach is to give a single equation for all flow regimes with a great accuracy. For example, for a pipe of circular crosssection, friction law takes the following mathematical form:
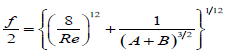 (2.3)
(2.3)
With,
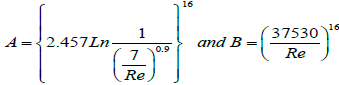 (2.4)
(2.4)
The following friction curves for all flow regimes were then plotted from a huge amount of experimental data.
To our knowledge, it is the only existing friction curves obtained in the same experimental conditions, i.e. the same pilot-plant, for several cross-section shapes, and covering laminar, transition and turbulent flow regimes. It clearly shows influence of the ducts cross-section shapes on flow stability characterized by critical Reynolds number Rec values.
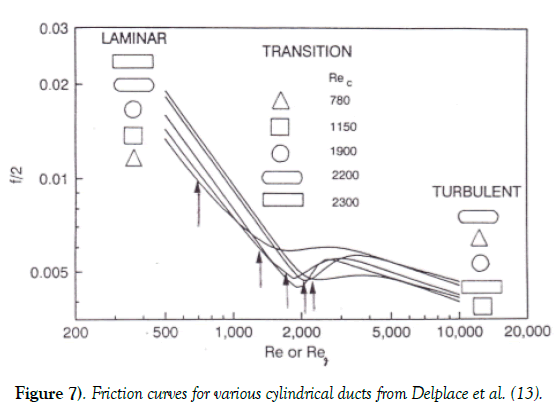
The less stable flow occurred in equilateral triangle duct Rec=780 and the most stable in the rectangular duct of aspect ratio 1:5 giving Rec =2300. In the laminar flow regime, all Poiseuille number (Po) values were of course in perfect agreement with Shah et al. [4] theoretical results.
Critical Reynolds Number Values, Poiseuille Number and Ducts Cross-Section Curvature
Critical Reynolds number and Poiseuille number values
As reported in the introduction of this paper, Poiseuille number is the product of friction factor and Reynolds number in the laminar flow regime. We called Po this dimensionless number defined by the following equation:
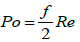 (3.1)
(3.1)
As showed in Figure 7, critical Reynolds number values seem to depend on Poiseuille number, moreover they follow the same tendency i.e. Rec increases when Po value increases.
Figure 7) Friction curves for various cylindrical ducts from Delplace et al. [13].
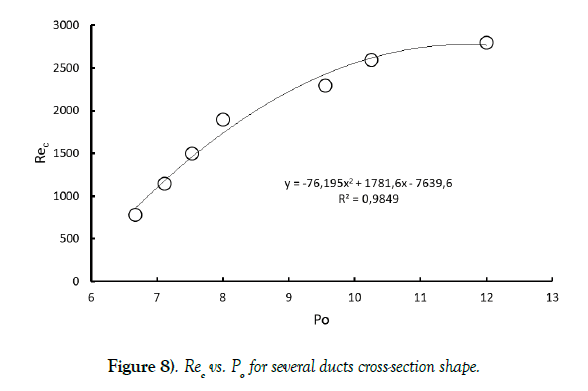
We decided then to add other data found in literature for Po and Rec values. From experimental work of Kao [19] performed in a rectangular duct of aspect ratio 1:8, we have Po=10.25 and Rec=2600. Recently, Marin et al. [20] numerically investigated the flow in a hexagonal duct. Their results indicate that pure laminar flow occurred below Re=2000 and a value of Rec=1500 could be used. From Shah et al. [4] work we have Po=7.53 for hexagonal ducts.
Finally, the well-known case of infinite parallel plates, often called plane Poiseuille flow, has to be considered. In that case, we know from theory that Po=12, but determination of Rec is always a great debate since the famous theoretical work of Lin [21] giving Rec=5360. The paper of Orszag [22] well discussed the problem and gave the value Rec=2800 as the most representative of “normal” conditions described in the introduction of this paper. All these couples (Po, Rec) were reported in the following graph.
Considering that determination of Rec values is subject to uncertainties, mainly due to experimental conditions (vibrations, pipes roughness…) and graphical determination (change in the laminar flow friction curve slope), we can consider that correlation of data presented in Figure 8 is quite acceptable. A quadratic form was used as a model available in the range of Poiseuille number values: 20⁄3 ≤ Po ≤ 12; 20⁄3 and 12 being respectively Po values for equilateral triangle and infinite parallel plates.
(Po, Rec) values presented in Figure 8, ask the question of PHE results described in the previous chapter. If we consider that maximum Poiseuille number value in a classical (regular) duct is 12 giving rise to the most stable flow and then to the highest critical Reynolds number around Rec = 3000; how can we interpret PHE results giving a very low value of Rec around 30 and a high value of Po around 15?
The typical shape of PHE friction curves without any brutal change in the slope in the transition flow regime as showed in Figures 5-7 can be found in packed and fluidized beds (McCabe 2001, Harrison et al.). Ergun type equations are widely used for that particular case and well known Kozeny- Carman equation gives:
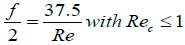 (3.2)
(3.2)
Which corresponds to results obtained in PHEs. This means that in PHE channels the flow is not free of obstacles like in classical ducts described above. The following picture (Figure 9) of flow patterns in a PHE channel with straight corrugations plates obtained by Delplace [12] during fouling experiments clearly showed the role of contact points between the plates.
Figure 9) Flow patterns in a PHE channel from Delplace [12].
This nice picture clearly demonstrated the role of instabilities created by the presence of obstacles (contact points between the plates) in the main flow stream; and also how eddies can be regularly distributed along the corrugated channel. From these observations and the particular shape of PHEs friction curves, it is clear that these ducts can not be considered as others (regular) previously described. Their hydrodynamical behaviour is more analogous to packed beds ones according to Kozeny-Carman and Ergun’s equations.
We will now consider classical (regular) pipes shapes reported in Figure 8 and how a geometrical approach could be a way to have a better understanding of flow stability in these ducts.
Critical reynolds numbers and ducts cross-section curvature
In a recent publication, Delplace [14] showed that Reynolds number can be seen as the ratio of curvatures. In that way of thinking, hydraulic radius was considered as the cross-section radius of curvature. It is then possible, for each shape previously studied, to calculate Reynolds number as followed:
Triangular duct- 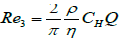 (3.3)
(3.3)
Square duct - 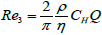 (3.4)
(3.4)
Circular duct - 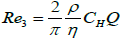 (3.5)
(3.5)
Rectangular ducts- 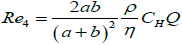 (3.6)
(3.6)
Infinite parallel plates 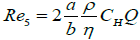 (3.7)
(3.7)
In these equations, 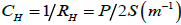 is the hydraulic curvature, with P(m) the cross-section perimeter and Sm2 its surface.
is the hydraulic curvature, with P(m) the cross-section perimeter and Sm2 its surface.
Of course, Re5 given by equation 3.7, comes from Re4 given by equation 3.6, with b≫a and Re2 given by equation 3.4, comes also from Re4 by considering a=b.
Q m3.s-1 is the volumetric flow-rate in the pipe.
Reynolds number takes then the following general form:
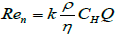 (3.8)
(3.8)
Where k is a real number depending on cross-section geometry characterized by its hydraulic curvature CH (m-1). For rectangles of aspect ratios 1:5 and 1:8 we obtain respectively: k=5⁄18 and k=16⁄81.
In another publication in applied Mathematics, Delplace [15] showed the great importance of isoperimetric theorem in the definition of hydraulic radius for a polygon or a polyhedron. In geometry, isoperimetric theorem explains that the discus always has the shortest perimeter for a given surface or the highest surface for a given perimeter when compared to all others geometries. This strong demonstrated mathematical theorem can be extended to higher dimensions. In 2D i.e. for surfaces, the often called isoperimetric quotient is defined by:
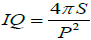 (3.9)
(3.9)
This dimensionless number is used to quantify the difference between the discus and all others planar geometries. For the discus we have IQ=1 which can be considered as the reference or ideal case. For all others compact geometries, IQ<1. The following Table 1 gives the values of parameter k and isoperimetric quotient IQ for all considered geometries.
| Geometry | k | IQ |
|---|---|---|
| △ | 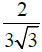 |
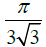 |
| ◻ | 1/2 | π/4 |
 |
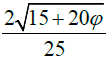 |
 |
 |
1/√3 | π/2√3 |
 1:5 |
5/18 | 5π/36 |
 1:8 |
16/81 | 8π/81 |
| ◯ | 2/π | 1 |
Table 1: Values of parameter k and isoperimetric quotient IQ ϕ ≅ 1.618 is the gold number
From these examples, it is self-evident that IQ = k (π/2)
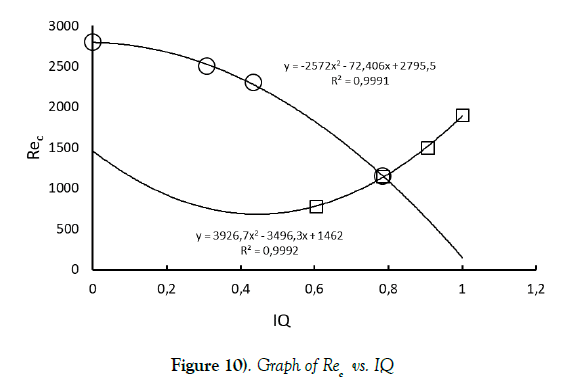
From equation (3.8), Reynolds number depends on k and then on IQ. We decided then to plot the graph Rec vs IQ for all geometries previously investigated.
Square symbols represent regular convex shapes i.e. equilateral triangle, square, hexagon and discus (IQ=1). Circular symbols represent rectangles, from the square to infinite parallel plates (IQ=0).
Two excellent correlations indicated in Figure 10 were obtained for the two curves maid of these symbols. The first one for regular convex shapes, the second one for rectangles. This approach seems to indicate that stretching of regular convex shapes increases flow stability and then critical Reynolds number value until it reaches a maximum value found for infinite parallel plates giving the most stable flow.
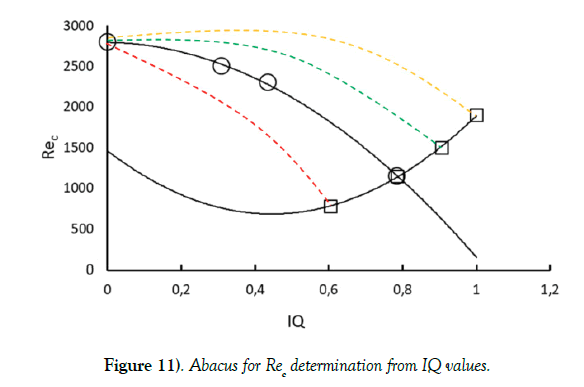
This graph could also be considered as an abacus giving critical Reynolds number values for a given regular duct cross-section characterized by its isoperimetric quotient IQ. The master curve corresponds to regular convex shapes obtained by increasing the number of sides: from equilateral triangle (3 sides) to the circle (infinite number of sides). The others curves describe each stretched geometry like rectangles. The following Figure 11 gives a representation of this possible abacus.
Red dotted line corresponds to triangles from equilateral ones, on the regular shapes master curve, to all isosceles triangles reaching infinite parallel plates.
Green dotted line describes hexagonal shapes, from regular hexagon, to infinite parallel plates by stretching two opposite sides.
Orange dotted line gives elliptical geometries, from pure circle to also infinite parallel plates.
In this representation, the plane Poiseuille flow appears the most stable giving the highest critical Reynolds number value according to Lin theoretical work [21].
As reported at the end of the introduction of this paper, isoperimetric theorem allowed to build this very simple and then practical abacus to determine fluids flow stability in ducts. Of course, at this time, there is a lack of data to enrich it. But, because of major interest of fluids flow stability for industrial applications, i.e. for heat and mass transfers applications; enrichment of this abacus by both experimental and numerical research works on the flow in ducts of various cross section shape should be performed.
Conclusion
In this paper, we investigated fluid flow stability in ducts of arbitrary crosssection shape. Our approach is based on a large amount of experimental results obtained by several authors and presented using correlations between Fanning friction factor and Reynolds number i.e. friction curves.
First of all, we showed the great importance of these experiments to accurately determine critical Reynolds number values and then the conditions where the flow stops to be purely laminar, i.e. where streamlines stops to be straight in the flow direction. For Reynolds number values greater than critical value, eddies form and then the flow becomes unstable. We are in the transition region. Experiments carried out in ducts having different cross-section shape with a large amount of measurements in the transition region are essential to understand phenomena.
From these results, we clearly established the major influence of ducts crosssection geometry in the transition between laminar and fully developed turbulent flow regime. The complex and particular case of industrial plate heat exchanger was also investigated and analysed. From flow patterns observations, their friction curves with very low critical Reynolds number values, and very high Poiseuille number values were explained. Plate heat exchangers flow passages have to be considered as made of obstacles and then very different than classical regular ducts. Their hydrodynamic behaviour is analogous to packed or fluidized beds giving friction curves with identical characteristics.
Considering 7 regular ducts, and famous Shah et al. [4] theoretical work giving Poiseuille number values, we obtained an acceptable correlation between Poiseuille numbers and critical Reynolds numbers experimentally determined. More experimental work is necessary to make this approach more accurate but the quadratic form proposed in this paper can be useful for a rapid determination of critical Reynolds number.
Finally, using recent theoretical work of Delplace [15] about curvature of polygons and polyhedral, we showed a strong correlation between critical Reynolds number value and isoperimetric quotient coming from famous isoperimetric theorem. Even if this approach has to be completed by experimental and numerical works on the flow in others geometries, it shows that an abacus of major interest in fluid mechanics and in industrial applications could be built.
REFERENCES
- Drazin PG. Introduction to hydrodynamic stability, Cambridge University Press. 2002. ISBN 0-521-00965-0.
- Trinh KT. On the critical Reynolds number for transition from laminar to turbulent flow, arxiv/1007.0810. 2010.
- Manish K, Dilbag SM, Satish U. Comparative analysis fully developed turbulent flow in various arbitrary cross-section ducts using finite volume approach. IRJET. 2017;4:2070-2074.
- Shah RK, London AL. Laminar flow forced convection in ducts. Academic Press. New York, San Francisco, London. 1978.
- Abou AO, El-Ajou A, Momani S. Constructing and predicting solitary pattern solutions for nonlinear time-fractional dispersive partial differential equations. J Computational Physic. 2015;293:385-399.
- Abou AO. Numerical solutions for the Robin time-fractional partial differential equations of heat and fluid flows based on the reproducing kernel algorithm. Int J Numerical Methods for Heat & Fluid Flow. 2017;28.
- Abou AO. Fitted reproducing kernel Hilbert space method for the solution of some certain classes of time-fractional partial differential equations subject to initial Neumann boundary conditions. Computers & Mathematics with Applications. 2017;73,1243-1261.
- El-Ajou, Abu AO, Momani S, et al. A novel expansion iterative method for solving linear partial differential equations of fractional order. Applied Mathematics and Computation. 2015;257;119-133.
- El-ajou, Abu AO, Momani S. Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: A new iterative algorithm. J Computational Physics. 2015;293:p 81-95.
- Cooper A, Usher JD. Plate heat exchangers: friction factor correlations– heat transfer correlations. Heat Exchangers Design Handbook. 1983.
- Leuliet JC. Comportement hydraulique et thermique des échangeurs à plaques traitant des produits non-Newtoniens. PhD Thesis. Henri Poincaré Univ. Nancy I. (1988).
- Delplace F. Identification des échangeurs à plaques. Application à l’encrassement par les produits laitiers. PhD Thesis. Henri Poincaré Univ.
- Delplace F, Delaplace G, Lefebvre S, et al. Friction curves for the flow of Newtonian and non-Newtonian liquids in ducts of complex cross-sectional shape. Proc. 7th International congress on engineering and food. Sheffield Academic Press. 1997;1;36-39.
- Delplace F. Reynolds number and spacetime curvature. Fluid Mech. Open Access. 2016;3:1.
- Delplace F. A new definition of curvature for polygons, convex polyhedra and hypersolids. IJSEAS. 2017;3:5.
- Delplace F, Srivastava HM. Rheology for the twenty-first century. Rheology Open Access. 2017;1:1.
- Joseph DD, Yang BH. Friction factor correlations for laminar, transition and turbulent flow in smooth pipes. Physica D: Nonlinear Phenomena. 2010;239:1318-1328.
- Churchill SW. Friction factor equation spans all fluid flow regimes. Chem Eng. 1977;7:91-92.
- Kao TW, Park C. Experimental investigations of the stability of channels flow. Part 1. Flow of a single liquid in a rectangular channel. J of Fluid Mechanics. 1970;43:145-164.
- Marin O, Vinuesa R, Obabko AV, et al. Characterization of the secondary flow in hexagonal ducts. Physics of Fluids. 2016;28:2-24.
- Lin CC. The theory of hydrodynamic stability, Cambridge University Press (1955).
- Orszag SA, Kells LC. Transition to turbulence in plane Poiseuille and plane Couette flow. 1980;96:159-205.