Newfound properties of specific functions and their coreflectives

Received: 20-Jul-2021 Accepted Date: Aug 03, 2021; Published: 10-Aug-2021, DOI: 10.37532/2752-8081.21.5.32

Citation: Estaik A. Newfound properties of specific functions and their coreflectives. J Pur Appl Math. 2021; 5(4):54:54.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

You will find definitions and behaviors of functions under specific change within themselves in this paper, written based on understanding from Adam Šesták, also written by Adam Šesták.

Commentary

Please note, that it would be appreciated for anyone to work on this subject and bring up some new information regarding these A-type functions.

Reflectable (A-type) functions:

A-type functions are functions which have a property of reflecting, not by having a minus sign in front of the function, but by changing something (not the minus) inside the function, which means, that odd functions cannot satisfy this requirement.

Definition:

f(g(x)) → -f(h(x))

|g(x)| ≠ |h(x)|

Note: g(x) has a different expression and meaning, than f(x). g(x) and f(x) are to f(x) are cooreflectives to each other, because they share the property of A-type functions, and are bonded by the terms in the definition.

Construction of A-type functions:

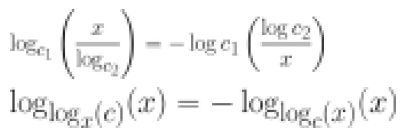
Examples:

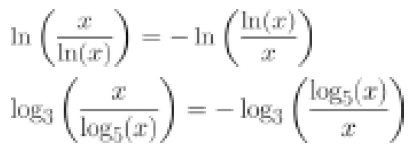
These are functions having this property. The last two are further construction to the first two.

They can be simplyfied to a form, which contains the first two ways, which A-type functions can be constructed in. These are observ Any values can be pluged as c, which means, that there are infinitely many of these functions, that can be constructed.

There are infinitely many such functions, as they can come from this function. We need to know however, if there are infinitely many functions that are completely different than the one shown. It was observed however, that it works only for logarithmic functions, but this statement has no proof. It appears that the log(x) function has some interesting characteristics, which clearly are visible now, since there are A-type functions. Maybe these characteristics can be found in a non- logarithmic function, but there has not been found an A-type function not being logarithmic in some way.

Application of this concept is not yet known, as it is first written on this new paper. It is good however, that there are now functions, which we can reflect without a minus sign. This does not imply, that we have changed the expression of the function, but its whole meaning. We haven’t found A-type functions, which are NOT logarithmic in any way. All these functions found having this property are in some way logarithmic, implying some new characteristic.

Graphs:

Usage: Usage of this concept is not yet known to anyone. The cause of this is the concept veing new and un-studied at this moment. It may be useful in some way, but we do not know the use yet. It would be great if we would find a good and remarkable application of this information.

Ending: There are such functions, which can behave as having a minus in front of them, without having the minus there, by changing components inside it, not by expression, but its pure meaning. These A-type functions have to be logarithmic, based on this observation. We however miss certainty, when we say it has to be at least in some way logarithmic, as there is no proof and this statement is based only on an assumption.

There are functions found, having this property. Also there are infinitely many of these functions.

I am hoping for more research on this topic and that people might find this useful. Maybe it can be used efficiently in an applied field, but this is just an assumption. I still want more research to be done to enlarge our understanding on this matter.

My thanks

“I would like to thank everyone for the support and encouragement given to me. I would also like to thank journals for making contributing more possible and easy.”

-Adam Šesták

People I am thankful to

Jan Šesták, Daniel Šesták, Hanka Šestáková, Alice Šestáková, Jana Šestáková, Alice Petrovičová, Jan Petrovič, Matěj Crhák, Anna Homolová, Darina Parmová, Timothy Mahurskyj, Pepa (Šedov) Dědek, Hugh Wallace and all the people with bright minds.