Number theory: A branch of mathematics

Received: 29-Dec-2023, Manuscript No. puljpam-24-6959; Editor assigned: 03-Jan-2024, Pre QC No. puljpam-24-6959 (PQ); Accepted Date: Mar 29, 2024; Reviewed: 05-Mar-2024 QC No. puljpam-24-6959 (Q); Revised: 17-Mar-2024, Manuscript No. puljpam-24-6959 (R); Published: 31-Mar-2024, DOI: 10.37532/2752-8081.24.8(2).01-04

Citation: Li S. Number theory: A branch of mathematics. J Pure Appl Math. 2024; 8(2):01-04.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

Number theory, a mathematical discipline focused on the characteristics of positive integers (1, 2, 3,...), often referred to as "higher arithmetic," stands as one of the oldest and most instinctive areas of mathematical exploration.

Throughout history, number theory has captivated not only professional mathematicians but also enthusiasts. Unlike some other mathematical fields, many of its problems and theorems can be grasped by individuals without extensive mathematical training. However, arriving at solutions and proofs often demands a high level of mathematical sophistication.

Key Words

Information flow; Energy; Validation; Indirect confirmation; Age of the universe; Dark energy

Introduction

Until the mid-20^th century, number theory was perceived as the most abstract realm of mathematics, seemingly detached from practical applications. However, the emergence of digital computers and digital communications unveiled its unexpected relevance to real-world issues. Simultaneously, advancements in computer technology empowered number theorists to achieve remarkable progress in tasks like factoring large numbers, identifying primes, verifying conjectures, and tackling numerical challenges that were once deemed insurmountable.

Contemporary number theory encompasses a diverse array of subfields, including elementary number theory, algebraic number theory, analytic number theory, geometric number theory, and probabilistic number theory. These subdivisions reflect various methodologies employed to address problems pertaining to integers.

From ancient times until Classical Greece

The ability to engage in counting traces back to prehistoric eras, as evidenced by archaeological findings such as a bone discovered in the Congo region of Africa, estimated to be around 10,000 years old, adorned with tally marks—an indication of an early ancestor's endeavors to quantify something. Even in the nascent stages of civilization, people had already grasped the concept of "multiplicity," marking the initial strides towards the exploration of numerical concepts.

Evidence suggests that an understanding of numbers thrived in ancient Mesopotamia, Egypt, China, and India, as demonstrated by the survival of tablets, papyri, and temple engravings from these early civilizations. Notably, the Babylonian tablet known as Plimpton 322 (circa 1700 BCE) exemplifies this. Utilizing modern notation, it presents number triples x, y, and z with the intriguing property that x²+y²=z². For instance, one such triple is 2,291, 2,700, and 3,541, where the equation 2,291²+2,700²=3,541² holds true. Such findings undoubtedly unveil a level of mathematical sophistication in ancient Babylon [1].

Despite these sporadic findings, there was no overarching theory of numbers. To find such a comprehensive framework—typical of theoretical mathematics—one must turn to the Classical Greeks. Their pioneering accomplishments showcased a unique amalgamation of the mystical inclinations of the Pythagoreans and the rigorous logic found in Euclid’s Elements [2, 3].

Pythagoras

As per tradition, Pythagoras (circa 580–500 BCE) conducted his work in southern Italy, surrounded by devoted followers. His philosophy elevated number to a fundamental concept essential for comprehending various phenomena, ranging from planetary motions to musical harmony. Given this perspective, it is unsurprising that the Pythagoreans attributed quasi-rational properties to specific numbers.
For instance, they placed importance on perfect numbers, defined as those equal to the sum of their proper divisors. Examples include 6 (whose proper divisors—1, 2, and 3—sum to 6) and 28 (1+2+4+7+14). Nicomachus of Gerasa, a Greek philosopher who flourished around 100 CE and was evidently influenced by Pythagoras' philosophy despite writing centuries later, suggested that perfect numbers symbolized qualities like "virtue, wealth, moderation, propriety, and beauty." (Modern scholars may dismiss such notions as numerical theology).

Similarly, the Greeks referred to a pair of integers as amicable, or "friendly," if each integer was the sum of the proper divisors of the other. They were acquainted with only one amicable pair: 220 and 284. It is easily verified that the sum of the proper divisors of 284 is 1+2+4+71+142=220, and likewise, the sum of the proper divisors of 220 is 1+2+4+5+10+11+20+22+44+55+110=284. To those inclined towards numerical mysticism, such occurrences may have appeared almost magical [4, 5].

Euclid

In contrast, Euclid approached number theory with a more straightforward style. Initiated this exploration by defining a number as "a multitude composed of units," with the plural form excluding 1; thus, for Euclid, 2 was the smallest "number." Subsequently, he defined a prime as a number "measured by a unit alone" (i.e., having only 1 as its proper divisor), a composite as any number that is not prime, and a perfect number as one equal to the sum of its "parts" (i.e., its proper divisors).

Building upon these foundations, Euclid established a series of theorems, marking the inception of number theory as a mathematical pursuit rather than a purely numerological endeavor. Notably, four propositions by Euclid stand out.

Firstly, Proposition introduces a method for determining the greatest common divisor of two whole numbers, a seminal contribution now honored as the Euclidean algorithm.

Secondly, Euclid presented a precursor of what is known as the unique factorization theorem or the fundamental theorem of arithmetic. This theorem asserts that every whole number can be uniquely factored into the product of prime numbers. For instance, 1,960=2 × 2 × 2 × 5 × 7 × 7 represents such a factorization, with no other valid decomposition possible. While Euclid's treatment of unique factorization falls short of modern standards, the essence of this concept can be discerned in Proposition.

Furthermore, Euclid demonstrated that no finite set of prime numbers encompasses all primes. His elegant proof, outlined in Proposition, stands as one of the most refined demonstrations in the realm of mathematics. Euclid's approach involved starting with any finite selection of primes—let's denote them as a, b, c, ..., n—and constructing a number by adding one to their product: N = (abc^...n) + 1. Subsequently, he scrutinized two possible scenarios:

1.Should N turn out to be a prime number, it would signifya fresh prime distinct from the set a, b, c, ..., n as itsurpasses all of them in magnitude. For instance,considering the original primes as 2, 3, and 7, the resultingN = (2 × 3 × 7) + 1 = 43 represents a larger prime.

2.Alternatively, in the event that N is composite, itnecessarily possesses a prime factor that, as shown byEuclid, cannot belong to the original set. For instance,starting with the primes 2, 7, and 11, we obtain N = (2 × 7× 11) + 1 = 155. Although composite, its prime factors, 5 and 31, are not part of the original set. Thus, in eitherscenario, a finite set of primes can consistently beexpanded. Consequently, through this elegant reasoning, itcan be deduced that the set of primes is infinite.

Number theory in the east

Automobile method is distributed by means of refuting the Goldbach Conjecture, while stating the Riemann Hypothesis may be stable in 3 dimensions. Thus we understand primes by geometrically weakoning the said saddle point by replacing its square value in an open line, that may have a boundary at D(0,0). This prime differential equation is explained where its dt value is the rate of change of prime equivalency −ΣN_T = b4.

We find meaning in this system. We will call it the boundary closure of equivalency

Goldbach Conjecture: a+b≠ 2N ≥4 (a,b prime) is found and thus refuted {A}= {a₁ = 2, a₂ = 5, a₃= 38, a₄ = 223, a₅ = 34}, {B} = {b₁ = -1, b₂ = -2, b₃= 5, b₄ = -8, b₅ = 13}

{T} produces these prime outputs

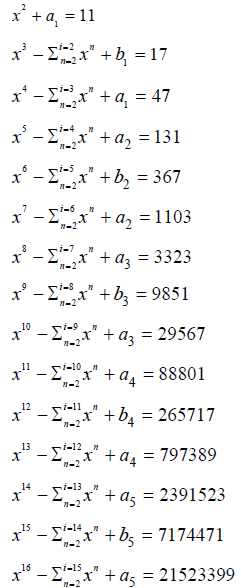
Homogeneous Riemannian Manifolds with Applications to Primes

This paper shows methods on how to reduce the Goldbach conjecture. In contrast, the conjecture is solved by definition that this eccentric proof will explain the seminal work of R. Knott in describing the one to one correlation of Fibonacci numbers and primes. This is done in an effort to further topological modeling and works of algebraic computational methods of abstract geometry and fractal imagery. Synthetic proofs are given by elementary procedure, and thus organic means. Perhaps later, a method like this will solve the Goldbach Conjecture or refute it 2NN A+B give insight into the Riemann Manifold defining (a, b) error.

The author does not claim proof but shows refutation through a stated method. By error analysis to begin.

The first part explains the aim of routing a line. The second part gives practical application and uses predictive models developed. The third part qualifies the use of immutable spaces. A statement of Poincare is made.

If the space does form two cubic-like structures: XYZ1 and XYZ2, through prime scalers, there is an empty space of fractal non zero curvature that cannot be separated from {A+B} through redirecting a sizable magnitude that is integrated. So any 1 unit space that is left an even area, includes two prime values of the minimal space that can be directly computed. Unless by non-euclidean geometry the projected point has nullity that scales towards infinity to refute. We use a bent lines, to redirect the formation of a distributed line, by primes, to a sphere.

<x> Prime routes follow this Riemman pattern analytically by rotational matrix 6.

Conclusion by Scientific Hypothesis

4D=64, a large distribution that finds dimensional understanding with 64-bit integers, memory addresses, or other data units are those that are 64 bits wide. A useful function that often approaches a maximum in our world. Let our symmetric value then round to 107. So we have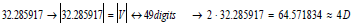

Examine this oddly gargatuent number:

1.4071371737173711909878900000100000000000000000000000000000000008

Now examine:

2.4071371737173711909878900000000000000000000000000000000000000008

This number is roughly 10⁶⁴ digits by base 10 standards that is our numerical stretch with regards to this paper.

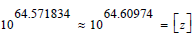
There is a set of 5{a+b} prime equations that fit this number: [z]

We should close the solution with reason on R₀

Let’s remind ourselves that the manifold is stretched by 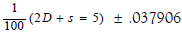the difference between r⁻ and r⁺. Analyzing two through super computing methods the two primes which sum (2) are:

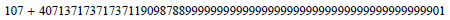
The useful idea is that a+b=(2) are the only primes that complete the sum. We can determine a prime limit by 2D−r given 2D−r=29 a prime. Inserting 1 into our prime at the digit limit of 29 back into (2) gives (1).

Notice 107 is found from the Fibonacci limit producing 106.5. It is clever that our a=107 and our b term ends in “1”. This refutes the Goldbach Conjecture. Notice how the span of 9 extends a great distance. It is a useful formula because we can limit the amount of primes within a digit gap. Now we close our assumption that our primes would behave this way given .08→ allows our assertion that the decimal bound is .00 in {T} = {S}.

Thus our rational data set of 13 or rad 13 flips “s” at an odd midpoint. It would make sense that it is refuted by (1) 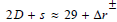the saddle point never sits on a Euclidean square.

The prime spaces are set apart by s+1=6, or a sphere pulled at a hexahedron to icosahedron stretch M0.

Thus concluding 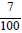strong metric for polynomial parameters inthe rational map. So the asymptotic limit line never divides degrees concerning 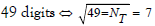that are beyond octahedron pull:

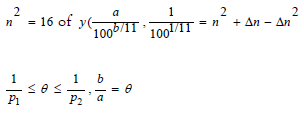
Only if:

Given F_SA = 8|2, and area F_V = 8 is parallel {T} so 16|2=8

By proof of linearity of 1-1 correspondence, the Goldbach Conjecture is proven false if the immutable space is projected onto Euclidean space with the measure returning the infinite radius simply as the ratio concerning either “a” or “b” imaginary, or not real. We have concluded it a non-complete tautology by the extra digit analogous to imaginary curve on the boundary line of degree n+1 digits connected on disk DR, and symmetry at 23 digits. 9 is marked on (1) and (2). So two prime spaces return the 3 manifold to a sphere.

We denote the prime limit, or prime digit gap, cubic-like. While one structure remains the other, 29- 23 = 6, defeats the minimal space needed to hold the additional prime evenly in Euclidean space. By platonic space and approximating error 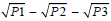, have allowed the 64 digit numeral to bound any possible 4-space. Then an n-1digit number, or 63 digit number contains no two primes or rate within the system. Every diagonal of polyhedra map out linearly a space of an even map until they converge by sphere point to a non-null space of the given topological cycle. The refutation by 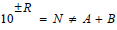of the inverse space is N=(1), which concludes:

The space R is homeomorphic on the 1-1 base of transformations limiting N_R = N_T.

Thus negating Goldbach. This strengthens Poincare.

We have proved Poincare is a stronger argument because the greater size the space becomes, the more dimensions or segments can reverse the transformation and make the geometry invertible.

Example: The volume of cylinder A is 108π, which is twice the volume of cylinder B. If the radius and height of A are the height and radius respectively of B, find the height of cylinder B.

Notice the way the problem is worded.

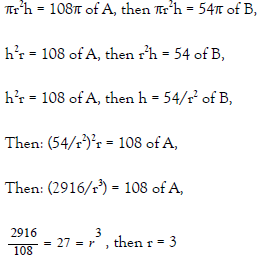
Then the height of B correlates 9h=54, so the height is 6, and we can conclude h=2r, or h=d, a diameter. We look at this idea in Refuting Logic of the Goldbach Conjecture in Riemann Analysis. We can reverse the process of embedding a triangle in the sphere with noting that the sector actually replaces the radian manifold, so the line of intersection describes the quality of geometry continuously. So while, A, B are not found in {A+B} by (1). The binomial effect of the species and the argument of 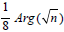shows that a fractal can engineer thelimits of a light dispersion, if matter does not intersect the point within the codirectional implication would be the same temperature, frequency, or wavelength : 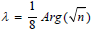So a cylinder transformsinto a sphere by its length conforming to the saddle point derivative of~ .RS Then this Riemann Space is homogenous to the manifold implied by 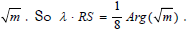Then by complex variablesheat is the imaginary component of a topology τ. Then A, B cylinders implies 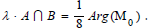This is the statement of the Poincarewith regards to the numerical compression of a sphere to a point in the 1-1 transformations implied by the geometry of the Fibonacci Sequence. Then the space would have to be the same in the initial disk translation.

Note: Integrating for color means we can express the coloration magnitude as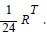

Direct Sphere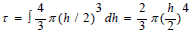

This should prove that every topological fiber bends at N_T = {1, -1,-6,5, 10,-1}

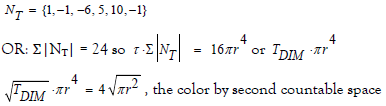
This relation is shown further in the author’s other paper:

Where meromorphic components are adjacent to the unit vectors by

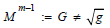
Theorem 1.0

R does not equal i in the prime number field given a local group of imaginary areas. That is in any group defined by {X} sets, finitely a triad. So a closed prime group is always found with a remainder term of 1 until the prime root is found and the remainder term is 0, or just a succession of n primes in a continuous {P}= n location.

This is shown with a basic smooth manifold and a rational smooth set, which is explored with variations in proving that R is not equal to i.

References

1. Mandelbrot B B. The fractal geometry of nature. New York: WH freeman. 1983;173(51).

   [Google scholar] [Crossref]

2. Falconer K. Fractal geometry: mathematical foundations and applications. John Wiley & Sons. 2004

   [Google scholar] [Crossref]

3. Knott R. The Fibonacci Numbers. The First 300 Fibonacci Numbers, Factored, University of Surrey. 2004

   [Google scholar] [Crossref]

4. Briggs J. Fractals: The Patterns of Chaos. London: Thames and Hudson. 1992:148.

   [Google scholar] [Crossref]

5. Vicsek. Fractal growth phenomena. Singapore/New Jersey: World Scientific. 1992: 139–46.

   [Google scholar] [Crossref]