On the coupling constant 3/2 of traditional kinetic theory of gases PV=E=3/2k_BT

Received: 28-Jun-2023, Manuscript No. PULJMAP-23-6563; Editor assigned: 30-Jun-2023, Pre QC No. PULJMAP-23-6563 (PQ); Reviewed: 13-Jul-2023 QC No. PULJMAP-23-6563; Revised: 03-Mar-2025, Manuscript No. PULJMAP-23-6563 (R); Published: 10-Mar-2025

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Description

The traditional kinetic theory of gases, which states that PV=E=3/2k_BT should be corrected to PV=E=k_BT, as the process that leads to the coupling constants of 3 and 1/2 has changed and is no longer necessary.

Kinetic theory of gases

The kinetic theory of gases deals with the volume, pressure, and energy related to the thermal behavior of gases in a closed space [1]. The most basic theory that explains this is given as follows:

PV=Ek=3/2k_BT                   (1)

Where,

P=Pressure, V=Volume, E_k=Kinetic energy, k_B=Boltzmann constant, and T= Temperature.

Here, the coupling constant 3/2 is considered an essential coupling coefficient that appears when deriving the ideal gas law [2-5]. However, regarding the coupling coefficient of 3, the text on the “Boltzmann constant”, the energy E_k is given by:

E_k=1/2 mv²=1/2k_BT              (2)

Therefore, considering translational motion as a one-dimensional motion along a straight path, the equation can be considered correct [6-10].

However, in reality, the velocity vector acting in a closed space acts perpendicular to the surface where the force acts. Therefore, the total acting area is not the cross-sectional area but the sum of the areas of the three surfaces [11-13]. This is why the coupling constant 3 needs to be removed and another reason is that the coupling constant 1/2 also needs to be removed [14].

Therefore, the kinetic theory of gases should be expressed as follows:

PV=E_k=k_BT                          (3)

Derivation

In a closed space (V=L³), the momentum of a moving object is expressed by Newton’s law of inertia as follows:

Where p is momentum, m₀ is the rest mass in the space, and ∼V is the average velocity.

When external pressure is applied, the momentum changes in conjunction with the change in velocity as follows:

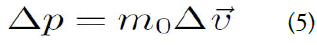
The change in distance is the distance that the velocity V moves during the time Δt, which is given by:

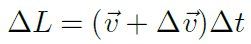
Where

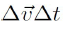
will be ignored due to very small quantity and t is given by:

From this, the change in force (ΔF) can be obtained as follows:

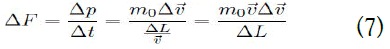
The pressure (P) is given as follows:

P=F/A                          (8)

Where A is the surface area of three sides of the closed space.

Rearranging equation (7), we get:

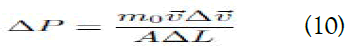
Integrating equation (10), we obtain:

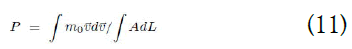
=E_k/V

Where,

And,

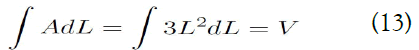
As the result, the correct theory that satisfies the ideal gas law is as follows:

PV=E=k_BT                          (14)

In consideration of relativistic time, by substituting the following equation into equation (6):

From (6) and the above, we have

We can obtain the following equation from equations (7), (10) and (12),

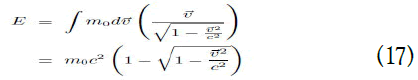
Here, if <

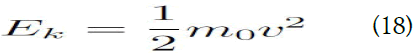
This is the exact expression for the traditional kinetic energy.

References

1. Wikipedia contributors. Ideal gas law. In Wikipedia, The Free Encyclopedia. 2024.
2. Wikipedia contributors. Boltzmann constant. In Wikipedia, The Free Encyclopedia. 2024.
3. Wikipedia contributors. Newton's laws of motion. In Wikipedia, The Free Encyclopedia. 2024.
4. Wikipedia contributors. Kinetic theory of gases. In Wikipedia, The Free Encyclopedia. 2024.
5. Wikipedia contributors. Pressure. In Wikipedia, The Free Encyclopedia. 2024.
6. Wikipedia contributors. Time dilation. In Wikipedia, The Free Encyclopedia. 2024.
7. Wikipedia contributors. Momentum. In Wikipedia, The Free Encyclopedia. 2024.
8. Wikipedia contributors. Energy. In Wikipedia, The Free Encyclopedia. 2024.
9. Wikipedia contributors. Mass–energy equivalence. In Wikipedia, The Free Encyclopedia. 2024.
10. Wikipedia contributors. Work (physics). In Wikipedia, The Free Encyclopedia. 2024.
11. Wikipedia contributors. Kinetic energy. In Wikipedia, The Free Encyclopedia. 2024.
12. Wikipedia contributors. Reaction (physics). In Wikipedia, The Free Encyclopedia. 2024.
13. Wikipedia contributors. Power (physics). In Wikipedia, The Free Encyclopedia. 2024.
14. Wikipedia contributors. Planck relation. In Wikipedia, The Free Encyclopedia. 2024.