On the Injectivity of an Integral Operator Connected to Riemann Hypothesis

Received: 12-Jul-2022, Manuscript No. puljpam-22-5145; Editor assigned: 13-Jul-2022, Pre QC No. puljpam-22-5145 (PQ); Accepted Date: Jul 28, 2022; Reviewed: 22-Jul-2022 QC No. puljpam-22-5145 (Q); Revised: 25-Jul-2022, Manuscript No. puljpam-22-5145 (R); Published: 30-Jul-2022, DOI: 10.37532/2752-8081.22.6(4).19-23

Citation: Adam D. On the Injectivity of an Integral Operator Connected to Riemann Hypothesis. J Pure Appl Math .2022; 6(4):19-23

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

The equivalent formulation of the Riemann Hypothesis (RH) given by Alcantara-Bode (1993) states: RH holds if and only if the integral operator on the Hilbert space L2 (0, 1) having the kernel function defined by the fractional part of (y/x) is injective. This formulation reduced one of the most important unsolved problems in pure mathematics to a problem whose investigation could be made by standard techniques of the applied mathematics.

The method introduced to deal with, is based on a result obtained in this paper: an operator linear, bounded, Hermitian on a separable Hilbert space strict positive definite on a dense family of including subspaces, subspaces on which the sequence of the ratios between the smallest and largest eigenvalues of the operator restrictions on the family is bounded inferior by a strict positive constant, is injective. Using a version of the generic method for integral operators on L2 (0, 1) we proved the injectivity of the integral operator used in the equivalent formulation of the RH.

Keywords

Approximation Subspaces, Integral Operators, Riemann Hypothesis.

Introduction

In his paper Alcantara-Bode proved (Theorem 1 pg. 152): the Riemann Hypothesis (RH) holds if and only if the following Hilbert- Schmidt integral operator T_ϕ defined on L² (0, 1) by:

has its null space 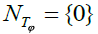where the kernel function is the fractional part function of the expression between brackets [1]. This integral operator has been introduced in (Beurling, 1955) for providing first equivalent formulation of RH [2], in terms of functional analysis. Beurling equivalent formulation of RH has been used by Alcantara- Bode in the second equivalent formulation of RH in terms of the injectivity of the operator in (1). The Alcantara-Bode formulation allows a different approach of the RH by using applied mathematics techniques in finding the injectivity of this integral operator. A very captivating view on RH could be found in [3].

We provide a method for investigating the injectivity of the linear bounded operators on separable Hilbert spaces using their approximations on dense families of subspaces. In this paper the norm used is the norm induced by the inner product. A dense family of finite dimension including subspaces is an infinite collection of subspaces {S_n}, n ≥ 2 in H, with the properties: S_n ⊂S_n+1, n ≥ 1 and 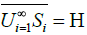. The idea behind this method is based on the following observations. If a linear, bounded operator T on H strict positive definite on a dense family of including subspaces has a zero, u ∈ N_T not null, it cannot be in any subspace of the family.

If 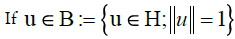is not in any subspace of the family, it has its orthogonal projections on the family {u_n}, n ≥ 1, verifying 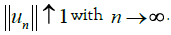. Because between the orthogonal projections of u and its residuum (u − u_n) there exists the following relationship 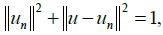there exists n₀ such that for n ≥ n₀, 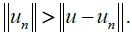. Now, if C is a constant > 0, there exists n1 such that 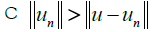once n > n1.

Or, as we proved, a such element u ∈ B could not be in the null space of the operator T, if C is a inferior bound of the set of the injectivity parameters of T, {μ_n}, n ≥ 1, parameters that are defined when T is also Hermitian, as the ratio between smallest and largest eigenvalues of the restrictions of T on the family’s subspaces.

Indeed, it follows from Lemma 1 that if u ∈ N_T ∩ B then 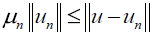on the approximation subspaces for n ≥ n₀ (u) and so, the sequence of the injectivity parameters {μ_n} must converge to 0 in contradiction with its inferior bounding by a strict positive constant C. So, we will set accordingly our working environment in order to build the method.

Observation 1. Suppose S is a subspace of a separable Hilbert space H on which T, an linear, bounded operator is strict positive definite: 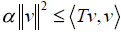for every v∈S. If there exists u ∈ N_T satisfying 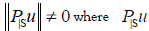is the orthogonal projection of u on S, then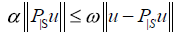

where ω > 0 verifies 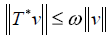for every v in S.

Proof. If u ∈ N_T then u ∈ H\S and 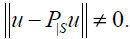If exists w ∈ S^⊥ such that Tw is not null and 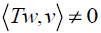, for every v not null ∈ S, then 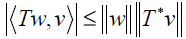. Taking 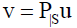and w = (v - u) follows 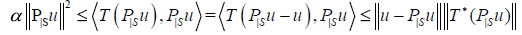proving the observation.

Let F = {Sn, n ≥ 1} a dense family of finite dimension including subspaces and denote L_F the class of the linear, bounded operators on H that are strict positive definite on every S_n ∈F. If T ∈ L_F for every v_n ∈ S_n, n ≥ 1 and for every S_n ∈F holds

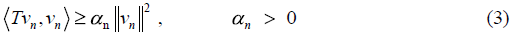
Applying the Observation 1 on the members of the dense family F follows:

Lemma 1. Let T∈ L_F. Suppose u ∈ N_T and denote ( ) :

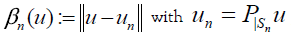
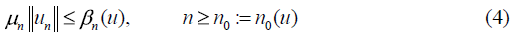
where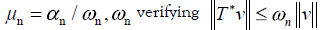 for every v ∈ S_n, n₀(u) being the index of the subspace from where the projections u_n are not null.

Proof. A such index n₀(u) there exists for every u because of the density of the family F in H adding, for n < n₀ (4) is trivial for every u and any subspace once the orthogonal projections are zero for n < n₀. The inequality follows applying the Observation 1 on each subspace Sn from the dense family.

A criteria for linear operators injectivity

Let T ∈ L_F. If u∈ N_T then 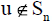, n ≥ 1, following 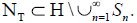We define the set of the eligible normalized zeros of the linear bounded strict positive operators on the family F by:

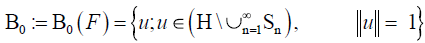
So, if u∈ N_T then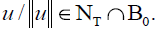

On the eligible set B₀ we consider the following expression:

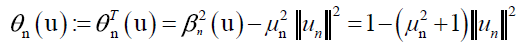
where we exploited the relationship for an eligible u between its orthogonal projection on Sn and its residuum (u - un),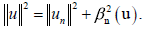

Theorem 1 (Injectivity Criteria). Let T∈ L_F. If there exists a strict positive constant C independent of n, such that μ_n(T)≥ C > 0 for every n ≥ 1, then T is injective.

Proof. Suppose that the sequence {μn}, n ≥ 1 is inferior bounded by a constant C independent of n, strict positive and let u ∈ B₀. If there exists an infinite subsequence of subspaces from the family for which

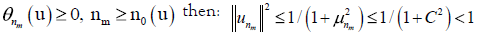and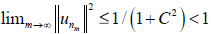

Or,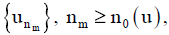, like {u_n}, n ≥ 1, should converge in norm to 1 on the approximation subspaces for every u ∈ B₀.

Thus, the inequality 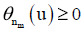could not take place on an infinity of subspaces of the family. We should have instead at most only a finite number of subspaces verifying it.

If there exists a finite number of subspaces on which 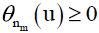n_m≥ n0(u) then there exists an index n1(u) such that we are in the situation θn(u) < 0 for every n ≥ n1(u).

If θn(u) < 0 holds for n ≥ n1(u), then 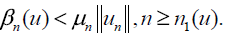But, u satisfying such relationship could not be in NT because a reverse inequality given by Lemma 1 holds for eligible u ∈ N_T. The only restriction we put on u ∈ H, has been its eligibility, u ∈ B₀. Thus, if {μn}, n ≥ 1 is inferior bounded, does not exists u ∈ B₀ that is in NT. Or, B₀ contains all normalized zeros of T, so N_T ={0} Q.E.D.

Lemma 2. If T is linear, bounded strict positive definite on F and the sequence of the injectivity parameters are bounded by a constant, then T is injective. This property is a immediate consequences of the property of boundness of T on H and so on every subspace of the family.

If T is not strict positive definite on F then we consider its associated Hermitian (T*T). If (T*T) is not strict positive definite on F then it has a zero in one of subspaces of F and so, T and (T*T) are not injective. While the strict positivity of the operator or of its Hermitian is mandatory for injectivity, the injectivity criteria Theorem 1 is only a sufficient condition as we observed from our example on the last paragraph.

Nowhere is included the Hermitian property in the proof of the Injectivity Criteria. We will replace the operator with its Hermitian when the original operator is not strict positive on the dense family of approximation subspaces or when we do not have enough information about its positivity - the reason is, both have the same null space and the Hermitian is positive definite on H.

When the linear operator T is Hermitian and strict positive on a dense family of finite dimension subspaces, then .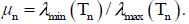

For showing it, it is enough to consider the finite dimension (sub)space S_n equipped with the orthonormal basis of the eigenfunctions of T_n in order to express α_n and ω_n function of the eigenvalues of T_n.

Approximations of the Integral Operators

Let consider in the separable Hilbert H:= L² (0, 1) the dense family of including finite dimension approximation subspaces 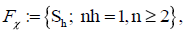where 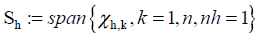spanned by indicator functions of disjoint intervals covering the domain (0,1):

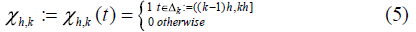
This family of approximation subspaces has been used in dealing with decay rate of convergence to zero of the integral operators’ eigenvalues, operators having the kernel functions like Mercer kernels [4], i.e. Hermitian and at least continue [5-7]. We will use this family for investigating the injectivity of the linear bounded integral operators. The family of functions {X_h,k }, k = 1,n, nh =1, defines a trace class integral operator with the kernel function 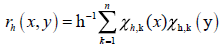that is an orthogonal projection in L² (0,1) on Sh having the orthogonal eigenfunctions {X_h,k } , k =1, n (see [5]). In fact, each S_h ∈ Fχ is generated by the families of the orthogonal eigenfunctions of the projection operator . 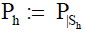Thus, the the kernel function ϕ of the linear integral operator

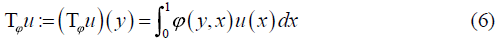
has the discrete approximations on Sh, nh = 1, n ≥ 2 given by [5]:

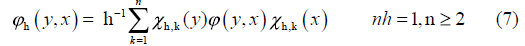
Observation 2. Taking a look at the kernel function ϕ_h , we observe that it is a sum of ’orthogonal piecewise functions’ once each term in the sum, 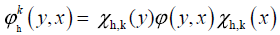k =1,n, nh =1 is zero valued outside the square 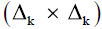. So, the matrix representation of the corresponding restriction operator will be 1- diagonal sparse matrix. The dense family has including finite dimensional subspaces, 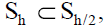, so, if the integral operators 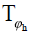having the kernel functions ϕ_h are strict positive definite then we fulfill the hypothesis of the Injectivity Criteria for the linear, bounded integral operator in (6). Thus we could proceed computing the components αh and ωh of their injectivity parameters {μh} (see, (4)) using the matrix representation of the restrictions of the operator 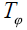on the finite dimension subspaces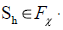

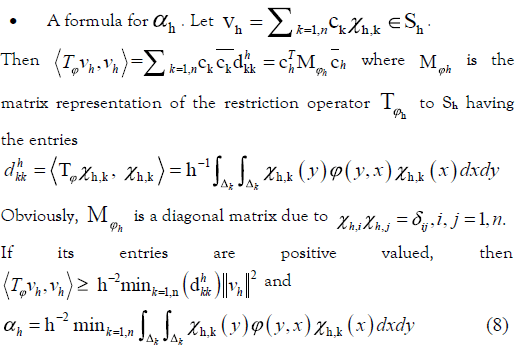
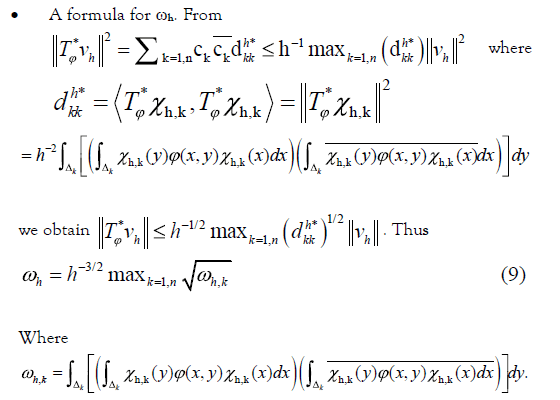
On Alcantara-Bode Hypothesis

The kernel function of the linear, bounded Hilbert-Schmidt integral operator in 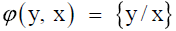as a function ∈ L²(0, 1)² is almost continue everywhere because its discontinuities lie on lines in (0,1)² of the form y=kx, k ∈N, that is a countable set of Lebesgue measure zero subsets and so, of Lebesgue measure zero and so will be the kernel of its associated Hermitian integral operator. In line with [5- 6] we will consider the dense family of approximation subspaces Fχ introduced in previous paragraph in order to investigate its injectivity. The entries of the diagonal matrix 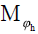, the representation of the restriction of the operator 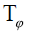on S_h defined by:

where γ is the Euler-Mascheroni constant . The sequence is monotone and converges to 0.5 for k → ∞. These entries are strict positive valued, bounded by 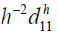and 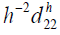, showing that 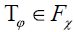having the strict positivity parameters given by

So, αh is a strict positive constant ∀n ≥ 2, nh = 1. We could apply Lemma 2 to obtain the injectivity without computing the ωh parameters knowing that T* is bounded. However, we will proceed with the computation of ωh (See the note from the next paragraph).

Taking in consideration that the kernel function of the adjoint operator is 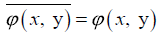verifies sup ({x/y})<1 on each square 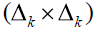of area h² , nh = 1, n ≥ 2, the integrals in ω_h,k are superior bounded by h, obtaining from (9) ω_h <1 and so, 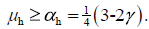Then, T_φ is injective due to the injectivity criteria.

Has no meaning to use the associated Hermitian operator once the operator is strict positive on Fχ and injective, both having the same null space.

Anyway, let’s consider the associated Hermitian operator 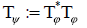of the integral operator in (1) having the kernel function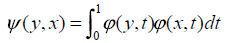

It is easy to observe that 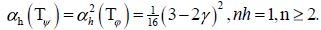So, 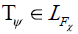is injective if we apply Lemma 2. On the other hand, 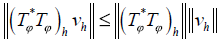shows that 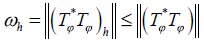is bounded by a constant as is α_h . Follows 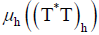is inferior bounded by a constant showing the injectivity of the operator avoiding Lemma 2. We just proved using the Injectivity Criteria:

Theorem 2. The linear bounded Hilbert-Schmidt integral operator T_φ on L² (0,1) having the kernel function the fractional part function

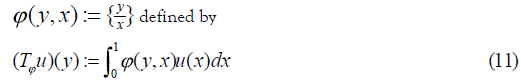
used for providing the equivalent formulation of Riemann Hypothesis [1], is injective, or equivalently, has the null space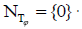

Some numerical aspects of the method

The method of operator projections using the finite rank operators associated to the family Fχ is backing up our choice to use the dense family for approximating the Beurling - Alcantara-Bode integral operator and we consider a consistent discretization approach. To justify the affirmation, let a kernel function on L²(0, 1)² and its approximations on Fχ be

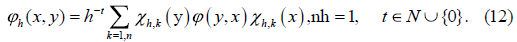
We observe from (8) and (9) that the injectivity parameters are independent of t by replacing h−1 with h−t. We find the kernel approximations for t = 0 in [6]. For t = 1 we find it in [5]. We have:

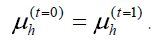
The injectivity criteria could be reformulated: if the components of the injectivity parameters alpha and omega are of the same order of h, then the linear operator is injective. This is the reason why Lemma 2 could be applied with caution choosing a consistent discretisation using orthogonal projection operators on approximation subspaces like in [5].

Observation 3. The following operator is injective having its injectivity parameters converging to 0.

The operator obtained as a product of identity by a power of x, I_s , s ∈ N on L²(0,1) as follows: for u ∈ L² (0,1)

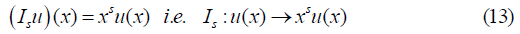
I_s is linear, bounded, strict positive definite and Hermitian on L²(0, 1) and so, strict positive on Fχ. The injectivity and positivity properties on H are coming from 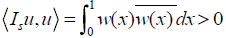for 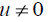where .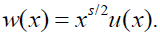

The components of the injectivity parameters using the theory exposed in the previous paragraphs are obtained as follows: given

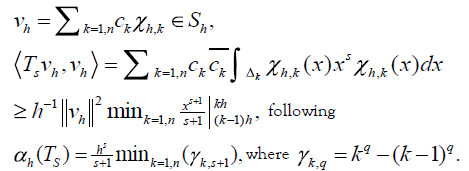
From

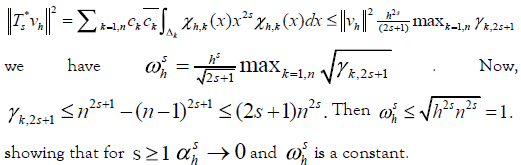
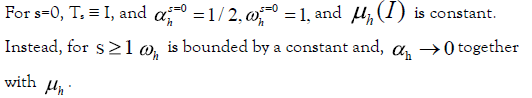
Thus: T_s , s ≥ 1, has its injectivity parameters violating the request of the injectivity criteria ( μ_h ≥ C ) showing that the injectivity criteria Theorem 1 is only a sufficient condition for the injectivity [8].

References

1. Alcántara-Bode J. An integral equation formulation of the Riemann Hypothesis. Integral Equ Ope Theory. 1993;17(2):151-68. [Google scholar]
2. Beurling A. A closure problem related to the Riemann zeta-function. Proc Natl Acad Sci.1955;41(5):312-14. [Google scholar] [Crossref]
3. Bombieri E. Problems of the millennium: The Riemann hypothesis. Clay Math Inst. 2000.  [Google scholar] 
4. Mercer J. Functions of positive and negative type, and their connection the theory of integral equations. Philosophical Transactions of the Royal Society A 209, 1909. [Google scholar] [Crossref]
5. Buescu J, Paixão AC. Eigenvalue distribution of Mercer‐like kernels. Math Nachr. 2007; 280:984-95.  [Google scholar]       [Crossref]
6. Chang CH, Ha CW. On eigenvalues of differentiable positive definite kernels. Integral Equ Oper Theory. 1999;33:1-7.  [Google scholar]     
7. Reade JB. Eigenvalues of positive definite kernels. SIAM J Math Anal. 1983;14(1):152-7. [Google scholar] [Crossref]
8. Adam D. On the Injectivity of an Integral Operator Connected to Riemann Hypothesis. [Crossref]