Oufaska's identity (Ɐn ε ℕ* we have ℼ2n)+π̅(2n)=n

Received: 07-Sep-2023, Manuscript No. PULJPAM-23-6699; Editor assigned: 11-Sep-2023, Pre QC No. PULJPAM-23-6699 (PQ); Reviewed: 25-Sep-2023 QC No. PULJPAM-23-6699; Revised: 18-Jan-2025, Manuscript No. PULJPAM-23-6699 (R); Published: 25-Jan-2025

Citation: Oufaska A. Oufaska’s identity (?n ? ?* we have ?(2n)+??(2n)=n). J Pure Appl Math. 2025;9(1):1-2.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Description

In this article, Oufaska’s identity (or Oufaska’s equation) asserts that for every natural number n the sum of the prime-counting function π(2n) and the con-counting function π(2n) equals n. Oufaska’s identity (or Oufaska’s equation) has many applications in number theory and its related to one of the famous problems in mathematics for example the twin prime conjecture [1-3].

Notation and reminder

^N* :={1,2,3,4,5,6,7,8,9,10,11,…} The natural numbers.

N_en :={0,2,4,6,8,10,12,14,16,18,20,…} The even numbers.

N_con :={9,15,21,25,27,33,35,39,45,49,51,…} The composite odd numbers.

P :={2,3,5,7,11,13,17,19,23,29,31,…} The prime numbers.

P∗ :={3,5,7,11,13,17,19,23,29,31,37,…} The odd prime numbers.

∀: The universal quantifier and ∃: The existential quantifier.

Card A: The number of elements in A.

A∩B: All elements that are members of both A and B.

A∪B: All elements that are members of both A or B.

∅: The empty set is the unique set having no elements.

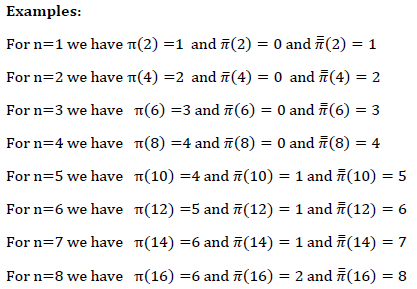
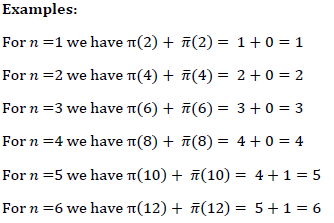
References

1. Chebyshev PL. On the function which determines the totality of prime numbers less than a given limit. Mem close Acad Imp Sci St Petersb. 1851;6:141-57.
2. Dickson LE. A new extension of Dirichlet’s theorem on prime numbers. Messenger Math. 1904;33(1904):155-61.
3. Hardy GH, Wright EM. An introduction to the theory of numbers. Oxford university press; 1979.

   [Google Scholar]