The Collatz Conjecture - From 1 To Infinity, No Loops, No Gaps, No Instability, P Vs NP, Halting Problem
Received: 01-Oct-2024 Accepted Date: Apr 21, 2021; Published: 30-Nov-2024, DOI: 10.37532/2752-8081.21.5.27
Citation: Clarke B. The Collatz Conjecture â?? From 1 To Infinity, No Loops, No Gaps, No Instability, P Vs NP, Halting Problem. J Pur Appl Math. 2024; 8(6):01-05.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
This paper describes the derivation of three functions that when used together generate all Collatz conjecture sequences starting from 1. Three functions are necessary as will become evident. The tree structure that is defined by the functions is fractal in nature and not like any other tree structure I have seen presented (Utube). Irrespective of issues of proof the definition of data structure has the potential to significantly impact current studies of the Collatz Conjecture. The work stands alone. There are no reference papers or associated organisations. The mathematics involved do not follow the general approach used by most mathematicians, in fact nothing more difficult than high school algebra is required. Even so the paper addresses the issues of potential loops, possible gaps and the question of possible instability. The P vs NP question and halting issues for computer searches are touched on. Potentially the major impact of this work is the implication that hailstone data sets are the outcome of several functions rather than the product of a single function. Two of the functions referred to above are closely related. The third is not
Introduction
My initial approach to the Collatz Conjecture was the same as most people, pick a number and generate a sequence heading to 1. After a few such numbers it becomes obvious that a tree structure is involved.
I decided to see if the problem could be approached from the opposite end. Accordingly I also decided that determination of the odd numbers was the key to the problem.
Data Generation
The tables below have been truncated to save space. There is enough information present to allow them to be extended indefinitely. The basic relationship of the Collatz Conjecture can be presented in two equations;
Equation 1: 3*A +1 = N A is odd, N is even.
Equation 2: N1 = N/2 N is even, N1 may be odd or even.
If N is even and not a straight power of 2 then on division by 2 a sufficient number of times you will arrive at an odd number.
So N can be represented as follows:
Equation 3: N = B*2^n B is odd
Substituting for N in equation 1 we get
Equation 4: 3*A + 1 = B*2^n
Transposing terms we get
Equation 5: A = (B*2^n -1)/3 A,B odd, n Є 1,2,3,…
So by selecting values for B and n we should be able to generate odd numbers for A which is shown in Table 1.
For a process supposed to generate odd integers this result looks a mess.
Data Analysis
By selectively removing elements of the table we can arrive at two reduced tables each containing only odd integers.
By inspection the following function can be arrived at:
Function 1:
[A1i] = ((3*p + 2)*2^n – 1)/3 p Є 1,3,5,… n Є 1,3,5,…
By inspection the following function can be arrived at:
Function 2:
[A2i] = ((3*p - 2)*2^n – 1)/3 p Є 1,3,5,… n Є 2,4,6,…
We now have two tables containing only integer values of odd numbers and the functions required to generate more odd numbers.
If [A1i] or [A2i] ≡ 1 (mod 3) then [A1i] or [A2i] can be substituted for [B2i]
If [A1i] or [A2i] ≡ 2 (mod 3) then [A1i] or [A2i] can be substituted for [B1i]
If [A1i] or [A2i] ≡ 0 (mod 3) then [A1i] or [A2i] cannot be used in Function 1 or Function 2
The values of [A1i] , [A2i] where [A1i] or [A2i] ≡ 0 (mod 3) are not discarded. Essentially we have a third function
Function 3:
[A3i] = [A1i]*2^n [A1i] ≡ 0 (mod 3) n Є 1,2,3,…
[A3i] = [A2i]*2^n [A2i] ≡ 0 (mod 3) n Є 1,2,3,…
Bearing in mind the above statements it is possible by using Functions 1, 2 and 3 to construct the Collatz Conjecture tree starting from 1.
Function 1: [A1i] = ((3*p + 2)*2^n – 1)/3 p Є 1,3,5,… n Є 1,3,5,…
Function 2: [A2i] = ((3*p - 2)*2^n – 1)/3 p Є 1,3,5,… n Є 2,4,6,…
Function 3a: [A3i] = [A1i]*2^n [A1i] ≡ 0 (mod 3) n Є 1,2,3,…
Function 3b: [A3i] = [A2i]*2^n [A2i] ≡ 0 (mod 3) n Є 1,2,3,…
Generation of data to allow construction of the Collatz Conjecture tree is shown in below Tables 4 & 5
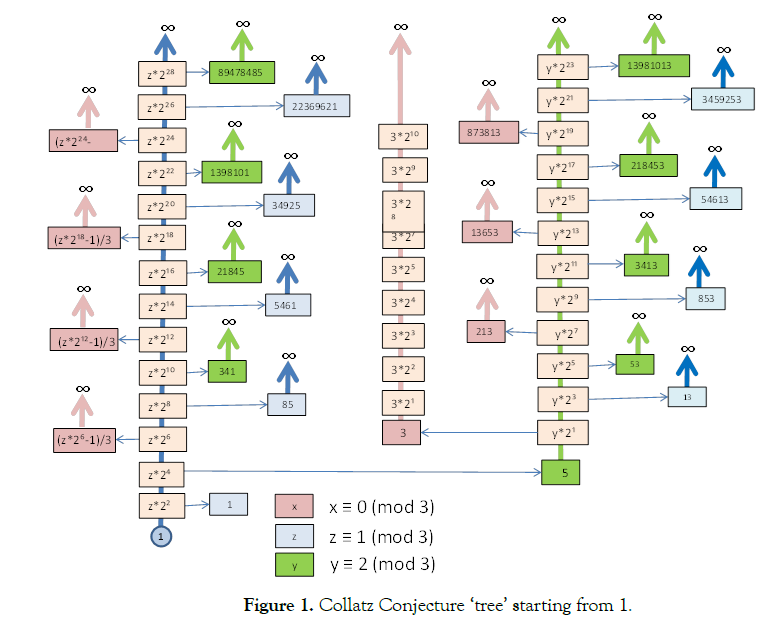
Collatz Conjecture ‘tree’ starting from 1
As shown in Figure 1 Every odd number is the root of a trunk of even numbers.
For trunks rooted on odd numbers such that [A1i], [A2i] ≡ 1 (mod 3) or [A1i], [A2i] ≡ 2 (mod 3) each even number shown in the diagram will give rise to a new odd number.
| n = | 1 | 2 | 3 | 4 | 5 | 6 |
| n^2 = | 2 | 4 | 8 | 16 | 32 | 64 |
| B | A | A | A | A | A | A |
| 1 | 0.333 | 1 | 2.333 | 5 | 10.333 | 21 |
| 3 | 1.667 | 3.667 | 7.667 | 15.667 | 31.667 | 63.667 |
| 5 | 3 | 6.333 | 13 | 26.333 | 53 | 106.333 |
| 7 | 4.333 | 9 | 18.333 | 37 | 74.333 | 149 |
| 9 | 5.667 | 11.667 | 23.667 | 47.667 | 95.667 | 191.667 |
| 11 | 7 | 14.333 | 29 | 58.333 | 117 | 234.333 |
| 13 | 8.333 | 17 | 34.333 | 69 | 138.333 | 277 |
| 15 | 9.667 | 19.667 | 39.667 | 79.667 | 159.667 | 319.667 |
| 17 | 11 | 22.333 | 45 | 90.333 | 181 | 362.333 |
Table 1 Calculated values of A.
For trunks rooted on odd numbers such that [A1i], [A2i] ≡ 0 (mod 3) there are no odd numbers associated with such even numbers.
Every odd number is the root of an infinitely long trunk of even numbers.
While the diagram only shows the powers of 2 necessary to construct the diagram, each trunk contains all the powers of 2. This will become obvious if you start with a number such as 218453 and apply the original Collatz Conjecture process.
Note: There are infinitely more even numbers than odd numbers.
The above diagram is just the start of an infinitely repeating structure
Can loops exist within the tree structure
For a loop to exist then a value of A calculated along one path has to equal the value of A calculated along a different path, or the value of B*2^n calculated on one path has to equal the value of B*2^n calculated along a different path.
Function 1: [A1i] = ((3*p + 2)*2^n – 1)/3 p Є 1,3,5,… n Є 1,3,5,…
Function 2: [A2i] = ((3*p - 2)*2^n – 1)/3 p Є 1,3,5,… n Є 2,4,6,…
Reframing the two functions gives us
Function 1a: [A1i] = ((3*p1 + 2)*2^(2n1+1) – 1)/3 p1Є 1,3,5,… n1Є 0,1,2,…
Function 2a: [A2i] = ((3*p2 - 2)*2^(2n2) – 1)/3 p2Є 1,3,5,… n2Є 1,2,3,…
Addressing the question of loops within the data structure:
For odd numbers the answer needs to cover the following:
Case 1: [A1i] = [A1j]
Case 2: [A2i] = [A2j]
Case 3: [A1i] = [A2j]
For even numbers where
[B1i] = (3*pi + 2)*2^ (2n1 + 1) piЄ 1, 3, 5, n1Є 0, 1, 2,
[B2i] = ((3*pi - 2)*2^(2n2) piЄ 1,3,5,… n2Є 1,2,3,…
[B3i] = [A1i]*2^n2 p Є 1,3,5,… n1Є 1,3,5,… n2Є 1,2,3,…
[B3j] = [A2j]*2^n2 p Є 1,3,5,… n1Є 2,4,6,… n2Є 1,2,3,…
We need to cover the following possibilities
Case 4: [B1i] = [B2i]
Case 5: [B1i] = [B1j]
Case 6: [B1i] = [B3i]
Case 7: B1i] = [B3j]
Case 8: [B1i] = [B3i]
Case 9: [B2i] = [B2j]
Case 10: [B2i] = [B3i]
Case 11: [B2i] = [B3j]
Case 12: [B3i] = [B3j]
Case 1: Can loops exist between values of A1: i.e. can [A1i] = [A1j]
Function 1: [A1i] = ((3*p + 2)*2^n – 1)/3 p Є 1,3,5,… n Є 1,3,5,…
When you construct a table of values for [A1] with B1 on one axis and 2^n on the other axis it becomes obvious that you cannot have two values of
A1 where B1i = B1j and simultaneously 2^n1 = 2^n2
Let
((3*pi + 2)*2^n1 – 1)/3 = ((3*pj + 2)*2^n2 – 1)/3 pi, pj Є 1,3,5,… n1, n2 Є 1,3,5,…
This becomes
(3*pi + 2)*2^n1 = (3*pj + 2)*2^n2 pi, pj Є 1,3,5,… n1, n2 Є 1,3,5,…
(3*pi + 2)/ (3*pj + 2) = 2^n2 / 2^n1 pi, pj Є 1,3,5,… n1, n2 Є 1,3,5,…
(3*pi + 2)/ (3*pj + 2) = 2^(n2 -n1) pi, pj Є 1,3,5,… n1, n2 Є 1,3,5,…
If pi = pj then LHS = 1, because pi = pj, n2 – n1 cannot equal zero, therefore RHS is either even or a real number
Ie. LHS does not equal RHS.
If n2 = n1 then (3*pi + 2) cannot be equal to (3*pj + 2)
So while the RHS equals 1 the LHS is either odd (and not equal to 1) or a real number.
Ie. LHS does not equal RHS.
Therefore all values of A1 are unique. Therefore no loops within A1.
Case 2: Can loops exist between values of A2
Function 2: [A2i] = ((3*p - 2)*2^n – 1)/3 p Є 1,3,5,… n Є 2,4,6,…
[A2i] = ((3*p - 2)*2^n – 1)/3 p Є 1,3,5,… n Є 2,4,6,…
Let
((3*pi - 2)*2^n1 – 1)/3 = ((3*pj - 2)*2^n2 – 1)/3 pi, pj Є 1,3,5,… n1,n2 Є 2,4,6,…
(3*pi - 2)*2^n1 = (3*pj - 2)*2^n2 pi, pj Є 1,3,5,… n1,n2 Є 2,4,6,…
(3*pi - 2)/ (3*pj - 2) = 2^n2/ 2^n1 pi, pj Є 1,3,5,… n1,n2 Є 2,4,6,…
(3*pi - 2)/ (3*pj - 2) = 2^(n2-n1) pi, pj Є 1,3,5,… n1,n2 Є 2,4,6,…
If (3*pi - 2) = (3*pj - 2) then LHS of equation = 1, RHS equals an even number or a real number.
If n2 = n1 then 2^(n2-n1) equals 1 and (3*pi - 2)/ (3*pj - 2) equals an odd number (not equal to 1) or a real number.
So all values of A2 are unique. Therefore no loops within A2.
Case 3: Can loops exist between values of A1 and A2:
Function 1: [A1i] = ((3*p + 2)*2^n – 1)/3 p Є 1,3,5,… n Є 1,3,5,…
Function 2: [A2i] = ((3*p - 2)*2^n – 1)/3 p Є 1,3,5,… n Є 2,4,6,…
Let
((3*pi + 2)*2^n1 – 1)/3 = ((3*pj - 2)*2^n2 – 1)/3 pi, pj Є 1,3,5,… n1 Є 1,3,5,… n2 Є 2,4,6,…
(3*pi + 2)*2^n1 = (3*pj - 2)*2^n2 pi, pj Є 1,3,5,… n1 Є 1,3,5,… n2 Є 2,4,6,…
(3*pi + 2)/(3*pj - 2) = 2^n2/2^n1 pi, pj Є 1,3,5,… n1 Є 1,3,5,… n2 Є 2,4,6,…
(3*pi + 2)/(3*pj - 2) = 2^(n2-n1) pi, pj Є 1,3,5,… n1 Є 1,3,5,… n2 Є 2,4,6,…
Can 3*pi + 2 = 3*pj - 2
3*pi + 2 = 3*pj - 2
4 = 3(pj – pi)
(pj - pi) = 4/3
Now pj and pi are integers and the difference has to be an integer therefore (3*pi + 2) cannot equal (3*pj - 2)
(n2-n1) can never be zero (n2 is even, n1 is odd), 2^(n2-n1) is either even or 1/(even number).
(3*pi + 2)/(3*pj - 2) is either an odd number or a real number. The equation can be arranged so the the RHS is an even integer while the LHS is odd or a real number.
Therefore there are no cases where a value of A1 equals a value of A2.
A corollary of the above is that all even numbers used to generate values of A1 and A2, are unique.
Given that all the powers of 2 are present in each trunk and the root of each trunk is a unique odd number then the even numbers in any trunk can be represented by the following:
N1i = B1i*2^n1, B1i ≡ 1 (mod 3), n1 Є 1,2,3,…
N2i = B2i*2^n, B2i ≡ 2 (mod 3), n1 Є 1,2,3,…
N3i = B3i*2^n B3i ≡ 0 (mod 3), n1 Є 1,2,3,…
All the questions of loops between even numbers can be reduced to the general case where two even numbers are created by multiplying two different odd numbers by a power of 2. The two odd numbers are different because all odd numbers created by Functions 1 and 2 are unique.
General case:
Can A*2^n1 = B*n^n2 where A ≠ B and A,B Є 1,3,5,… n1, n2 Є 1,2,3,…
Let A*2^n1 = B*n^n2
Then
A/B = 2(n2-n1)
A/B is either an odd integer (not equal to 1) or a real number, 2(n2-n1) is either 1 or an even number or the reciprocal of an even number.
If n1 > n2 then the equation can be restated as B/A = 2^(n1-n2) in which case B/A equals an odd integer or a real number and 2^(n1-n2) is an even number.
Therefore A*2^n1 ≠ B*2^n2
From the above none of the even numbers in the Collatz Conjecture tree are duplicated.
Therefore there are no loops between even numbers.
Therefore there are no loops in the Collatz Conjecture tree.
The Gaps issue: Do the two functions below calculate all the odd numbers ?:
Function 1: [A1i] = ((3*p + 2)*2^n – 1)/3 p Є 1,3,5,… n Є 1,3,5,…
Function 2: [A2i] = ((3*p - 2)*2^n – 1)/3 p Є 1,3,5,… n Є 2,4,6,…
Consider
Function 1: [A1i] = ((3*p + 2)*2^n – 1)/3 p Є 1,3,5,… n Є 1,3,5,…
[A1i] = ((3*(2n1+1) + 2)*2^(2n2+1) – 1)/3 n1 Є 0,1,2,… n2 Є 0,1,2,…
[A1i] = (3*(2n1+1)* 2^(2n2+1) + 2*2^(2n2+1) – 1)/3 n1 Є 0,1,2,… n2 Є 0,1,2,…
[A1i] = (3*(2n1) )* 2^(2n2+1) + 3* 2^(2n2+1) + 2*2^(2n2+1) – 1)/3 n1 Є 0,1,2,… n2 Є 0,1,2,…
[A1i] = (2n1) * 2^(2n2+1) + (5*2^(2n2+1) – 1)/3 n1 Є 0,1,2,… n2 Є 0,1,2,…
[A1i] = n1 * 2^(2n2+2) + (5*2^(2n2+1) – 1)/3 n1 Є 0,1,2,… n2 Є 0,1,2,…
For any given value of n2 the above equation can be restated as
Function 1b: [A1i] = k1*n1 + k2 n1 Є 0,1,2,…
Where k1 = 2^(2n2+2) k2 = (5*2^(2n2+1) – 1)/3 n2 Є 0,1,2,…
Consider
Function 2: [A2i] = ((3*p - 2)*2^n – 1)/3 p Є 1,3,5,… n Є 2,4,6,…
[A2i] = ((3*p - 2)*2^n – 1)/3 p Є 1,3,5,… n Є 2,4,6,…
[A2i] = ((3*(2n1 + 1) - 2)*2^(2n2) – 1)/3 n1 Є 0,1,3,… n2 Є 1,2,3,…
[A2i] = ((3*(2n1)*2^(2n2) + (3 - 2)*2^(2n2) – 1)/3 n1 Є 0,1,3,… n2 Є 1,2,3,…
[A2i] = (2n1)*2^(2n2) + (2^(2n2) – 1)/3 n1 Є 0,1,3,… n2 Є 1,2,3,…
[A2i] = 2^(2n2+1)*n1 + (2^(2n2) – 1)/3 n1 Є 0,1,3,… n2 Є 1,2,3,…
Function 2b: [A2i] = k3*n1 + k4 n1 Є 0,1,3,…
Where k3 = 2^(2n2+1) k4 = (2^(2n2) – 1)/3 n2 Є 1,2,3,…
If you select an odd number N, then to number of odd numbers from 1 to N is given by (N + 1)/2.
In order to use functions 1b and 2b to calculate the number of odd numbers in tables 2 and 3 it is necessary to redefine the work space.
Function 1a: [A1i] = k1*n1 + k2 n1 Є 0,1,2,…
Where k1 = 2^(2n2+2) k2 = (5*2^(2n2+1) – 1)/3 n2 Є 0,1,2,…
Function 2a: [A2i] = k3*n1 + k4 n1 Є 0,1,3,…
Where k3 = 2^(2n2+1) k4 = (2^(2n2) – 1)/3 n2 Є 1,2,3,…
For Table 2
For any given value of n2 the number of odd numbers present between 1 and N is given by
Let m1’ = (N-k2)/k1
m1 = Int(m1’)
The number of odd numbers for a given value of n2 is
N(n2) = m1 + 1
For Table 3
| n = | 1 | 3 | 5 | |
| n^2 = | 2 | 8 | 32 | |
| p | [B1i] = 3p + 2 | [A1i] | [A1i] | [A1i] |
| 1 | 5 | 3 | 13 | 53 |
| 3 | 11 | 7 | 29 | 117 |
| 5 | 17 | 11 | 45 | 181 |
Table 2 Values of [A1i].
| n = | n = | 2 | 4 | 6 |
| n^2 = | n^2 = | 4 | 16 | 64 |
| p | [B2i] = 3p - 2 | [A2i] | [A2i] | [A2i] |
| 1 | 1 | 1 | 5 | 21 |
| 3 | 7 | 9 | 37 | 149 |
| 5 | 13 | 17 | 69 | 277 |
Table 3 Values of [A2i].
Generation of data to allow construction of the Collatz Conjecture tree:
From Function 2: [A2i] = ((3*p - 2)*2^n – 1)/3 p Є 1,3,5,… n Є 2,4,6,…
For p = 1,
| n | 2^n | [B2i] = 3p - 2 | N = [B2i] *2^n | [A2i] = (N-1)/3 | [A2i]≡0 (mod3) | [A2i]≡1 (mod3) | [A2i]≡2 (mod3) |
| 2 | 4 | 1 | 4 | 1 | 0.333 | 0 | -0.333 |
| 4 | 16 | 1 | 16 | 5 | 1.667 | 1.333 | 1 |
| 6 | 64 | 1 | 64 | 21 | 7 | 6.667 | 6.333 |
| 8 | 256 | 1 | 256 | 85 | 28.333 | 28 | 28.667 |
| 10 | 1024 | 1 | 1024 | 341 | 113.667 | 113.333 | 113 |
| 12 | 4096 | 1 | 4096 | 1365 | 455 | 454.667 | 454.333 |
| 14 | 16384 | 1 | 16384 | 5461 | 1820.333 | 1820 | 1820.667 |
From Function 1: [A1i] = ((3*p + 2)*2^n – 1)/3 p Є 1,3,5,… n Є 1,3,5,…
For p = 1,
| n | 2^n | [B2i] = 3p + 2 | N = [B2i] *2^n | [A2i] = (N-1)/3 | [A2i]≡0 (mod3) | [A2i]≡1 (mod3) | [A2i]≡2 (mod3) |
| 1 | 2 | 5 | 10 | 3 | 1 | 0.667 | 0.333 |
| 3 | 8 | 5 | 40 | 13 | 4.333 | 4 | 3.667 |
| 5 | 32 | 5 | 160 | 53 | 17.667 | 17.333 | 17 |
| 7 | 128 | 5 | 640 | 213 | 71 | 70.667 | 70.333 |
| 9 | 512 | 5 | 2560 | 853 | 284.333 | 284 | 283.667 |
| 11 | 2048 | 5 | 10240 | 3413 | 1137.667 | 1137.333 | 1137 |
| 13 | 8192 | 5 | 40960 | 13653 | 4551 | 4550.667 | 4550.333 |
m2’ = (N-k4)/k3
m2 = Int(m1’)
N(n2) = m2 + 1
The maximum value of n2 is exceeded when N(n2) equals zero.
Summing all the values for N(n2) returns a result equal to the number of odd numbers from 1 to N.
N can take any positive odd integer value.
This implies that there are no gaps in the odd numbers from 1 to N.
As I cannot prove this algebraically it will have to stand as Alf’s conjecture.
Stability
The question of stability is usually raised in connection to applying the Collatz Conjecture process to a preselected number and seeing if it reduces to 1.
If you choose a number and then start following the path down the structure there is only one way to go. There are no loops or cross connections.
Accordingly there can be no instability in the process. Once you pass from one trunk to the next you never return to the previous trunk.
The P vs NP question
Using the conventional approach to creating a Collatz Conjecture sequence can result in the sequence reaching a value several hundred times the size of the starting number. The number of steps between starting the calculation and reaching this high point is unpredictable. The number of steps from the high point to the final outcome ( reaching 1) is also unpredictable.
When starting from 1 you immediately have an infinite number of even numbers to choose from to create the next odd number. Once you select an even number and create the next odd number you again have an infinite number of even numbers to select from in order to create the next odd number from. And so it goes for every odd number you create. In trying to get to 41 you are faced with making this choice 39 times. So 39 times in a row you have to choose the right number out of an infinite number of possible numbers. The chance of correctly choosing the right sequence of numbers to reach 41 is (1/∞)^39, ie your chance of correctly choosing the right path is infinitesimal.
However if you have the solution having worked it out the normal way then it is childs play to map the solution to the Collatz Conjecture structure defined by Functions 1, 2 and 3.
Thus checking a solution is very easy, creating a solution starting from 1 is impossible in most cases.
The Collatz Conjecture structure starting from 1 is an ever dividing tree without any cross connections. Every time you select an even number to reach the next odd number you have an infinite number of wrong choices available but only one right choice. Once you step off the correct path you can never regain it.
The halting problem.
When starting from 1 to find a selected number it is unknown as to what the maximum value of the sequence will be. It is also unknown as to how far beyond the maximum value you have to go to find the selected number. Thus there is no easily defined halting criteria for a search along any given path.
If you choose to search along every path for a fixed distance before moving to the next path the issue becomes the rapid multiplication of possible paths. In many cases it will be required to do several extensions of the distance covered by the search resulting in the number of possible paths expanding extremely rapidly.
It would not be difficult to select a number for which halting is unlikely to occur.
Conclusion
The functions described in this paper allow the calculation of the Collatz Conjecture data set starting from 1. Issues of stability and whether or not any given sequence decays to one become irrelevant.
By changing the solution space from a rectangular table to the space between half an inverted parabola and the two axis, the problem of gaps in the data set disappear. As the value defining the shape of the parabola can take any value short of infinity then this approach truly defines all the possible Collatz Conjecture sequences.
While I have not read the paper produced by Sir Bryan Thwaites I believe this approach addresses the gaps issue raised in that paper.