The parameterization of all stabilizing minimum-phase controllers for minimum-phase strictly proper plants
2 Department of Electrical and Electronic 1 Posts and Telecommunications Institute of Technology, Vietnam, Email: nghiamt@ptit.edu.vn
3 Division of Mechanical Science and Technology, Gunma University, Kiryu 376-8515, Japan, Email: k-hashikura@gunma-u.ac.jp
Received: 10-May-2023, Manuscript No. puljpam-23-6440; Editor assigned: 12-May-2023, Pre QC No. puljpam-23-6440 (PQ); Accepted Date: May 29, 2023; Reviewed: 14-May-2023 QC No. puljpam-23-6440 (Q); Revised: 16-May-2023, Manuscript No. puljpam-23-6440 (R); Published: 31-May-2023, DOI: 10.37532/2752-8081.23.7(3).193-199
Citation: Zhang D, Mai NT, Hashikura K, et al. The parameterization of all stabilizing minimum-phase controllers for minimum-phase strictly proper plants. J Pure Appl Math. 2023:7(3);193-199.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
The problem of parameterization is to find all stabilizing controllers for the controlled system. At present, there are many methods to choose from for the controlled plants with the minimum-phase. However, most of the existing procedure do not introduce minimum-phase controller into the system. In this sense, Zhang et al. have a new view that a parameterization method for all steady- state minimum phase controllers for minimum phase biproper systems is given. This paper expands the research results of Zhang et al. for the minimum-phase strictly proper controlled systems and the parameterization of all minimum-phase stabilizing controllers is given. The internal stability and control performance of the closed-loop system are studied. At the same time, an algorithm which can be used to construct minimum phase stability control is presented. Finally, an example is given to explain the characteristics of the algorithm proposed in this paper. Because this method can find all the minimum-phase stabilizing controllers well, it can be applied to many control problems.
Keywords
Minimum-Phase System; Minimum-Phase Controllers; Strictly Proper Plants; Closed-Loop Characteristics .
Introduction
For the minimum-phase strictly proper controlled system, the parameter expressions of minimum-phase stabilizing controllers are given in this paper. That is, this paper proposes the parameterization of the minimum-phase stabilizing controllers for the minimum-phase system. The problem of parameterization is to find all stablizing controllers for a plant, so as to make the system stable, and to obtain plants those can be stabilized [1-11]. This method can effectively solve all the parameterization of the minimum-phase stabilizing controllers for minimum-phase system, so it has been applied in many practical problems.
Compared with the non-minimum phase system, the minimum-phase system has fast response, small energy delay, stable inverse system and other advantages [12-13]. Comparing with the nonminimumphase system constructed by configuring the right half-plane zero point or adding the time-delay, it is obtained that the minimumphase system has the shortest response time [13]. At any time, the cumulative output energy of the minimum phase system is not less than that of the non-minimum phase system. It can be proved that the cumulative output energy of the minimum phase system is closer to time 0 and has the shortest energy delay [12]. And the inverse system of the minimum-phase system is stable, because the stable poles of the inverse system of the minimum phase system is the zeros of the original system which has no unstable zero. Benefiting from these advantages, the minimum-phase system is widely used in signal processing and other related fields, such as state system, design of causal stable digital filter, neural network and calculation and processing of cepstrum and inverse filtering [12-16].
Glaria and Goodwin provided a simple parameterization for the stability control of the minimum-phase [4]. However, there are two difficult problems. One of them is that the parameterization of stabilizing controllers proposed by Glaria and Goodwin usually contain improper controllers. In the specific process of use, a proper controller is needed. Second, the internally stability in the system is not parameterized. In order to solve the above problems, Yamada presents a parameterization for the class of all proper stabilizing controllers for linear minimum phase systems [5]. Parametric processing is carried out by using all the stabilizing controllers, such as all stabilization modification of the minimum-phase object, repetitive control, adaptive control, model feedback control, parallel compensation technology, PI control and PID control [5, 17-23]. For multiple-input/ multiple-output systems, a parameterized scheme of all stability control is given, and the research results of these schemes can be extended to multiple-input/multiple-output [17-24].
However, for the minimum-phase plants, there is still a problem whether its stability control can be used by the minimum-phase controller. If the stabilizing controller with nonminimum-phase is used, its unstable zeros will cause the transfer function of the closed-loop system to have zeros on its right half plane. This makes the closed-loop control system very sensitive to the disturbance of the external environment, thus affecting the control effect. In addition, if the feedback loop is truncated, that is, it is split into a feedforward, then the instability caused by it will lead to instability [7,8]. In this way, even though the controlled plant is of minimum-phase, the control system becomes an nonminimum system. If the minimum-phase control is adopted, the target of the minimum-phase will remain unchanged, and the magnitude of sensitivity of the whole system will become small. The lower the sensitivity curve, the greater the damping to external interference. If the minimum-phase controllers of the minimumphase plants can be parameterized, a new control strategy for the minimum-phase system can be obtained. Therefore, for the strictly proper controlled plants with minimum-phase, the minimum-phase controllers must be parameterized.
In this paper, we propose the parameterization of all stabilizing minimum-phase controllers for minimum-phase strictly proper plants. That is, we consider the parameterization that the stabilizing controller makes minimum-phase plant stable, which the stabilizing controller is of minimum-phase. Analysis of the internal stability and control characteristics of closed-loop system are provided. We also present a design method of the minimum-phase stabilizing controllers that contributes to the construction of a minimum-phase closed-loop system. In addition, we show a numerical example to illustrate the characteristics of the proposed design approach.
Problem Description
In this section, we introduce the problem considered in this paper. We consider a closed loop feedback control system as,

Here, y(s) ∈R(s), u(s) ∈R(s), r(s) ∈R(s) and R(s) are the output, control input, reference input and disburtance of the control system respectively. G(s)∈R(s) and C(s)∈R(s) are the controller and the plant of the control system separately, and both of them are of minimum-phase, that means, all zeros of them are in the left half plane. In this paper, the controlled plant G(s) with minimum-phase is required to be strictly proper and it is possible to be stable or unstable. By using the parameterization of the minimum-phase stabilizing controller for the minimum-phase plant, the controller C(s) is required to be derived. In the specific process of use, a proper controller is needed and the internally stability and the robustness of the control system need to be considered. Here R(s) indicates the set of real rational functions for the set with s.
Before seeking the parametrization for the strictly proper plants, the preliminary result proposed by Zhang et al. is summarized [25]. For the minimum-phase biproper plants, the parameterization of all minimum-phase stabilizing controllers are given as follows.
Lemma 1
G(s) is assumed to be of minimum-phase and to be biproper [25]. Then the minimum-phase controller C(s) stabilizes the feedback control system in (1) if and only if C(s) is written by the form of

where Q(s) ∈ RH∞ is any minimum-phase function to make (1- Q(s)) G(s) ∈ RH∞ . RH∞ denotes the set of stable rational function with s [25].
The problem considered in this paper is to clarify the parameterization of all stabilizing minimum-phase controllers C(s) for minimum-phase strictly proper plants G(s).
The Parameterization of all Stabilizing Minimum-Phase Controllers for Minimum-Phase Strictly Proper Plants
In this section, we clarify the parameterization of all stabilizing minimum-phase controllers C(s) for minimum-phase strictly proper plants G(s).
This parameterization is summarized in the following theorem.
Theorem 1
Assume that G(s) is strictly proper and of minimum-phase. When K(s) exists in a system of equations, K(s) is a stable and biproper real rational function and make G(s) + K(s) be a biproper and minimumphase real rational function. Utilizing the above K(s), for all proper minimum-phase stabilizing controllers C(s) of the plant G(s) with strictly proper and minimum-phase, the parameters are as follows
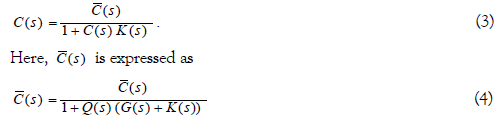
and 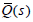 is the minimum-phase function belong to RH∞ and to make
is the minimum-phase function belong to RH∞ and to make 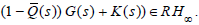
For proving the Theorem 1, the following theorems are needed.
Theorem 2
Assume that G(s) is strictly proper and minimum-phase. When K(s) exists in a system of equations, K(s) is a stable and biproper real rational function and make G(s) + K(s) be a biproper and minimum phase real rational function.
Proof
At first, G(s) is factorized into the coprime factors with N(s) ∈ RH∞ and D(s) ∈ RH∞ on RH∞ and G(s) is rewritten in the form of

Here, because G(s) is assumed to be of minimum-phase and strictly proper, N(s) ∈ RH∞ is of minimum-phase and strictly proper. In addition, G(s) + K(s) is donated as
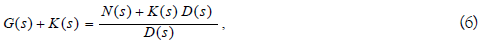
Then, the exist condition of K(s) is that G(s) + K(s) is a biproper and minimum-phase, and consistent with that of U(s)∈u and

Here, u is the set of unimodular functions on RH∞ , so U(s)∈u implies U (s)∈ RH∞ and U-1(s) ∈RH∞. The existence conditions of U(s) and K(s) is equivalent to the interpolation problem and are written as
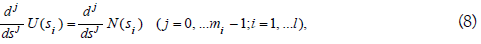
where s1, ...,sl are different zeros of D(s) on the positive real axis, m1, ...,ml are the corresponding multiplicities and l denotes the number of different zeros of D(s) on the positive real axis. Since G(s) is of minimum-phase, N(s) is also of minimum-phase. This implies that all of N(si) are the same sign. From Theorem 2.3.1, there exists U(s) ∈u and K(s) ∈RH∞ satisfying (8) [7]. This implies that there exists U(s)∈u and K(s) ∈RH∞ satisfying (7).
The remaining problem is whether or not, K(s) is biproper. Next, it is shown that if U(s)∈u exists such that (7) holds true, then K(s) is biproper. From (7), K(s) is written by

The assumption that U(s) holds (7) implies that K(s) written by (9) is stable. Since both U(s) and D(s) are biproper and N(s) is strictly proper, K(s) denoted by (9) is biproper.
We have thus proved the theorem.
Theorem 3
Assume that 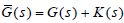 is the real rational function with
strictly proper and minimum-phase. All minimum-phase stabilizing
controllers
is the real rational function with
strictly proper and minimum-phase. All minimum-phase stabilizing
controllers 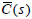 , its parameterization for the plant
, its parameterization for the plant 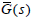 is denoted as
is denoted as

Here, 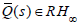 is any minimum-phase function and to make
is any minimum-phase function and to make 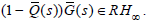
Proof
Because 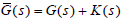 is assumed to be the real rational function
with strictly proper and minimum-phase, according to Lemma 1, the
minimum-phase stabilizing controllers
is assumed to be the real rational function
with strictly proper and minimum-phase, according to Lemma 1, the
minimum-phase stabilizing controllers 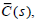 its parameterization for
its parameterization for 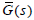 is denoted as (10).
is denoted as (10).
We have thus proved the theorem.
Theorem 4
Assume that K(s) ∈ RH∞ is biproper and G(s) is strictly proper. If the
minimum-phase controller C(s) stabilizes the plant G(s), then 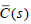 is
written as
is
written as

stabilizes the plant 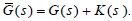 Furthermore, the opposite is
also true. That is, if the minimum-phase controller
Furthermore, the opposite is
also true. That is, if the minimum-phase controller 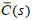 stabilizes the
plant
stabilizes the
plant 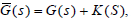 , then the the minimum-phase controller
C(s) is written as
, then the the minimum-phase controller
C(s) is written as

stabilizes the plant G(s).
Proof
First, we will prove that if the minimum-phase controller C(s)
stabilizes G(s), then the minimum-phase controller 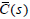 written by
(11) stabilizes
written by
(11) stabilizes 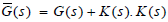 is assumed to be biproper and
C(s) is assumed to be of minimum-phase. In (11) if the
(1 - C(s)K(s))-1 has unstable zeros, the unstable zeros are the unstable
poles of C(s). Therefore, the
is assumed to be biproper and
C(s) is assumed to be of minimum-phase. In (11) if the
(1 - C(s)K(s))-1 has unstable zeros, the unstable zeros are the unstable
poles of C(s). Therefore, the 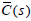 has no unstable zeros, that is,
has no unstable zeros, that is, 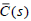 is of minimum-phase. Then from (11) and simple manipulation,
is of minimum-phase. Then from (11) and simple manipulation, 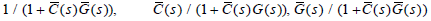 and
and 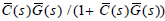 are rewritten as
are rewritten as
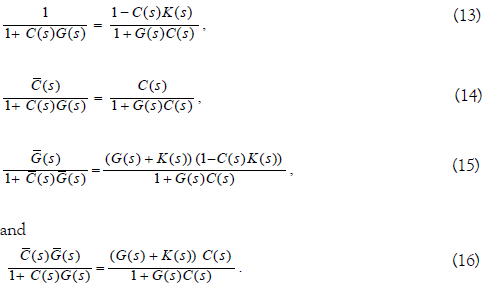
From the assumption that C(s) stabilizes G(s), 1 / (1 + C(s)G(s)), C(s) / (1+ C(s)G(s)), G(s) / (1+C(s)G(s)), and C(s)G(s) / (1 +C(s)G(s)) are all include in RH∞ . Therefore, all of transfer functions in (13),
(14), (15) and (16) are include in RH∞.
Next, we will show that if the minimum-phase controller 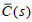 stabilizes the plant
stabilizes the plant 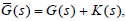 then the minimum-phase
controller C(s) written by (12) stabilizes G(s). In (12) if the
then the minimum-phase
controller C(s) written by (12) stabilizes G(s). In (12) if the 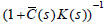 has unstable zeros, the unstable zeros are the unstable
poles of C(s). Therefore, the C(s) has no unstable zeros, that is, C(s) is
of minimum-phase. Then from (12) and simple manipulation, 1 / (1+C(s)G(s)), C(s) / (1+C(s)G(s)), G(s) / (1+C(s)G(s)) and C(s)G(s) / (1+C(s)G(s)) are rewritten as
has unstable zeros, the unstable zeros are the unstable
poles of C(s). Therefore, the C(s) has no unstable zeros, that is, C(s) is
of minimum-phase. Then from (12) and simple manipulation, 1 / (1+C(s)G(s)), C(s) / (1+C(s)G(s)), G(s) / (1+C(s)G(s)) and C(s)G(s) / (1+C(s)G(s)) are rewritten as
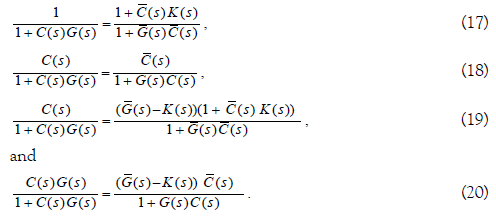
From the assumption that 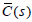 stabilizes
stabilizes 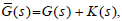
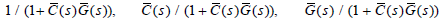 and
and 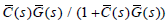 are all include in RH∞ .
Therefore, all of transfer functions in (17), (18), (19) and (20) are include in RH∞ .
are all include in RH∞ .
Therefore, all of transfer functions in (17), (18), (19) and (20) are include in RH∞ .
We have thus proved Theorem 4.
Theorem 1 is proved using the above-described theorems.
Proof
From Theorem 2, there exists biproper K(s) ∈ RH∞ to make 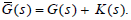 of minimum phase. From Theorem 4, the
parametrization of all internally stabilizing controllers C(s) for G(s) is
same to that of all internally stabilizing controllers
of minimum phase. From Theorem 4, the
parametrization of all internally stabilizing controllers C(s) for G(s) is
same to that of all internally stabilizing controllers 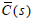 for
for 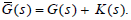 The parametrization of all internally stabilizing controllers
The parametrization of all internally stabilizing controllers 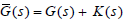 is given by (10), where
is given by (10), where 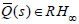 is
any minimum-phase function to make
is
any minimum-phase function to make 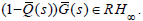 The
equation (10) corresponds to (4). From Theorem 4, using
The
equation (10) corresponds to (4). From Theorem 4, using 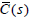 , C(s)
is written in terms of (12). The equation (12) corresponds to (3). The
proof of Theorem 1 is complete.
, C(s)
is written in terms of (12). The equation (12) corresponds to (3). The
proof of Theorem 1 is complete.
Properties of the Control System
We elucidate the properties of the closed-loop control system using the parameterization of all the stabilizing minimum-phase controllers given by (3) in this section.
First, we consider the reference tracking property. Here, using the parameterization of all minimum-phase stabilizing controllers for the minimum-phase plants in (3), the transfer function in (1) from the reference input r (s) to the output y(s) of the control system is given as

Therefore, in order to make the output y(s) follow the step reference input without steady-state error,

must be achieved. Thus, the output y(s) follows the step reference
input r(s) =1 / s without steady-state error, if 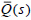 satisfies the
following condition
satisfies the
following condition

Next, the decay properties of the disturbance are described. The transfer function from the disturbance d(s) to the output y(s) is given as

Therefore, in order to fully decay the step disturbance d (s) =1 / s,

must be achieved. Thus, the step disturbance of d (s) =1 / s, will
effectively be rejected if 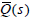 satisfies the following condition
satisfies the following condition

Design Method of Minimum-Phase Stabilizing Controllers
Next, we present a design method of the stabilizing minimum-phase
controllers for the minimum-phase strictly proper plants. From
Theorem 1, to design a minimum-phase stabilizing controller C(s), we
need to obtain K(s) satisfying Theorem 2 and such that 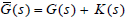 is of minimum-phase and biproper. Then,
is of minimum-phase and biproper. Then, 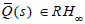 is determined as a function of any minimum-
phase such that
is determined as a function of any minimum-
phase such that 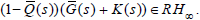 Furthermore, in
order to make the output y(s) follow the reference input
r(s) = 1/s without steady-state error,
Furthermore, in
order to make the output y(s) follow the reference input
r(s) = 1/s without steady-state error, 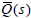 needs to satisfy (23). A
design method for Q(s)∈ RH∞ and the minimum-phase
stabilizing controller C(s) is concluded as follows.
needs to satisfy (23). A
design method for Q(s)∈ RH∞ and the minimum-phase
stabilizing controller C(s) is concluded as follows.

Numerical Example
This section shows a numerical example to illustrate the features of the proposed design method.
Consider the problem to find a minimum-phase stabilizing controllers for the plant G(s) written by

Then the minimum-phase stabilizing controller C(s) is obtained as
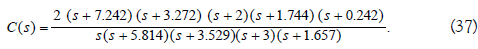
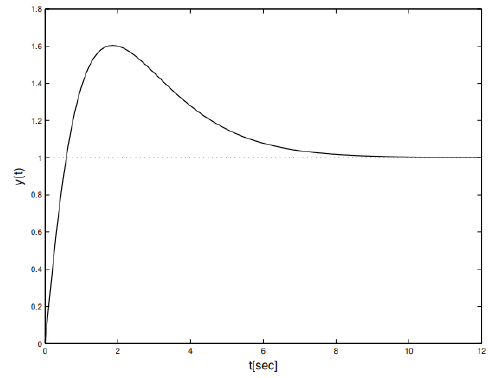
For the step reference input r(t) = 1, the output of the closed-loop system y(t) reacts as follows 1 when using the minimum-phase stabilizing controller C(s) (37). In the curve of Figure 1, it is proved that the controlled system is stable under the equation (1), and its output y(t) is equal to the step reference input r(t) = 1, and there is no steady-state deviation.
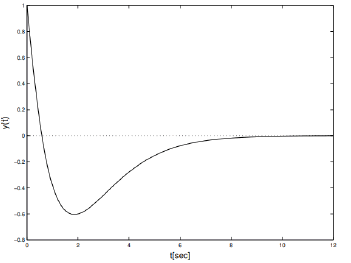
On the contrary, if there is a step disturbance, the output response of the closed-loop is displayed in the Figure 2. The curve in Figure 2 confirms which the effect of this interference on d(t) = 1 is effective.
Next, to verify the robustness of the proposed method, we consider this case where we control a perturbed controlled plant with the controller that has been derived. The controlled plant is denoted as

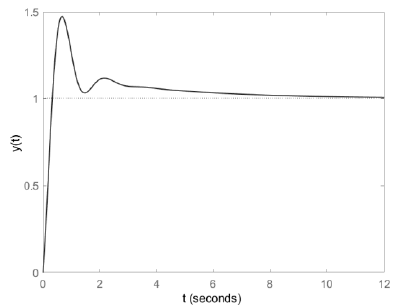
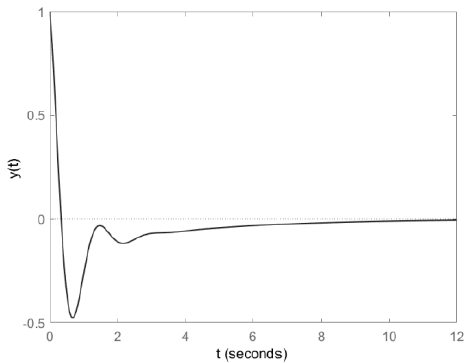
In this case, the output response corresponding to the step input r(t) = 1 is represented in Figure 3. The figure reflects that output y(t) follows the step reference input r(t) well with no steady state error. And the output response corresponding to the step disturbance d(t) = 1 is represented in Figure 4. The figure reflects the ability to effectively stop external disturbance.
Conclusion
In this paper, we clarified the parameterization of all stabilizing minimum-phase controllers for minimum-phase strictly proper plants. That is, we showed that if the stabilizing controller C(s) is written by the form of (3), the minimum-phase plant is stabilized. In addition, we showed a numerical example to illustrate that a stabilizing minimum-phase controller written by the form of (3) can stabilize the minimum-phase plant. In the future, we will present the parameterization of all stabilizing minimum-phase controllers for minimum-phase mutiple-input/mutiple-output plants.
References
- Youla DC, Jabr HA, Bongiorno JJ. Modern Wiener-Hopf design of optimal controllers. Part I: The single-input-output case. IEEE Trans Autom Control. 1976;21(1):3-13.
- Desoer CA, Liu RW, Murray J, et al. Feedback system design-The fractional representation approach to analysis and synthesis. IEEE Trans Autom Control. 1980;25(3):399-412.
- Zhou K, Doyle JC, Glover K. Robust and optimal control. Prentice-Hall. 1980.
- Glaria JJ, Goodwin GC. A parametrization for the class of all stabilizing controllers for linear minimum phase systems. IEEE Trans Autom Control. 1994;39(2):433-34.
- Yamada K. A parameterization for the class of all proper stabilizing controllers for linear minimum phase systems. IFAC Proc Vol. 2001;578-83.
- Zames G. Feedback and optimal sensitivity: model reference transformations, multiplicative seminorms and approximate inverses. IEEE Trans Autom Control. 1981;26(2):301-20.
- Vidyasagar M. Control System Synthesis: A Factorization Approach. Morgan Claypool. 2011.
- Akuzawa T, Zhang D, Hoshikawa T. et al. A Design Method for Strongly Stabilizing Controllers. Int J Innov Comput Inf Control. 2020;16(6):2131-41.
- Zhang D, Hashikura K, Suzuki T, et al. The characteristic of all strongly stabilizable MIMO plants. ICIC Express Lett. 2019;13:601-07.
- Hagiwara T, Yamada K, Sakanushi T, et al. The parameterization of all plants stabilized by Proportional controller. 25th Int Tech Conf Circuit/Syst Comput Commun CD-ROM. 2010;76-8.
- Hoshikawa T, Li J, Tatsumi Y, et al. The class of strongly stabilizable plants. ICIC Express Lett. 2017;11:1593-98.
- Kulkarni A, Isabelle SK, Colburn HS. On the minimum-phase approximation of head-related transfer functions. Proc 1995 Workshop Appl Signal Process Audio Accoustics. 1995;84–7.
- Franklin GF, Powell JD, Emami NA. Feedback control of dynamic systems. Prentice hall. 2002.
- Dam HH, Nordebo S, Svensson L. Design of minimum-phase digital filters as the sum of two allpass functions using the cepstrum technique. IEEE Trans Signal Process. 2003;51(3):726–31.
- Blaauw M. Modeling timbre for neural singing synthesis: methods for data-efficient, reduced effort voice creation, and fast and stable inference. Univ Pompeu Fabra. 2022.
- Modern Wiener-Hopf design of optimal controllers. Part I: The single-input-output case.
- Okuyama T, Yamada K. A parameterization for the class of all stabilizing repetitive learning controllers for linear minimum phase systems. Proc IEEE conf Syst Man Cybern. 1999;5:62-67.
[Google scholar] [Crossref] [Google scholar] [Crossref]
- Yamada K. Control structure of stabilizing controller for the minimum phase systems and design method of adaptive control systems. IFAC Proc Vol. 2001;597-602.
- Yamada K, Satoh K, Matsushima N. A design method of adaptive control systems using the parametrization of all stabilizing controllers for minimum phase systems. Intell Eng Syst Through Artif Neural Netw. 2004;14:379-384.
- Yamada K, Moki T. Relation between Model Feedback Control Systems and parameterization of all stabilizing controller. IFAC Proc Vol. 2002.
- Yamada K, Moki T. A study on control design methdo using parallel compensation technique. Trans Jpn Soc Mech Eng. 2003;69(687):3015-20.
- Yamada K. A design method for PI control for minimum phase systems. Intell Eng Syst Through Artif Neural Netw. 2003;13:571-76.
- Yamada K. Modified PID controllers for minimum phase systems and their practical application. Proc 2005 Electr Eng/Electron Comput Telecommun Inf Technol (ECTI) Int Conf Vol. II of II. 2005;457-460.
- Yamada K, Satoh K, Mei Y, et al. The parametrization for the class of all proper internally stabilizing controllers for multiple-input/multiple-output minimum phase systems. ICIC Express Lett. 2009;3(1):67-72.
- Zhang D, Hashikura K, Kamal MAS, et al. The parameterization of all stabilizing minimum-phase controllers for minimum-phase plants. ICIC Express Lett. 2020;14(10):979-84.