The Photon Gas in the Quantized Friedmann Universe
Received: 21-Jul-2023, Manuscript No. puljmap-23-6608; Editor assigned: 23-Jul-2023, Pre QC No. puljmap-23-6608(PQ); Accepted Date: Aug 10, 2023; Reviewed: 28-Jul-2023 QC No. puljmap-23-6608(Q); Revised: 01-Aug-2023, Manuscript No. puljmap-23-6608(R); Published: 15-Aug-2023, DOI: 10.37532. /puljmap.2023 .6(3); 01-03
Citation: Collier R. The Photon gas in the quantized Friedmann universe. J Mod Appl Phys. 2023, 6(3):1-3
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
A semi classical fundamental equation of quantum gravitation is applied to a flat Friedmann universe containing a photon gas. The mean energy of a photon is determined by the method of canonical partition and the classical one-particle state function for the ideal photon gas. For very high temperatures, there is a deviation from the classical equipartition theorem
Key Words
Semi classical quantum gravitation; Friedmann universe; Planck´s radiation law; statistical canonical partition
Introduction
If, on the smallest spatial and temporal scales, the universe has a grainy structure, Planck’s electromagnetic radiation law ought to have a modified structure, too. Radiation propagating over a spacetime range that has a lattice structure will not be able to fall below a bottom limit of the particle wavelength and, thus, will also have to maintain an upper limit of the particle energy.
For the theoretical implementation of this idea there are several approaches. The most difficult problem is encountered in supporting these investigations by a generalized special theory of relativity that would permit an invariant limit for a minimum limit unit of length or a maximum of particle energy. We refer to Ref and, especially for the thermodynamics of the photon gas, to [1-10]. To extricate ourselves us from these principal problems, let us first look for a first correction of Planck`s radiation formula as it would appear, e.g., in a quantized Friedmann universe
The hamiltonian operator
Let our investigations start from the Hamiltonian operator of matter in a flat Friedmann universe. In (Ref) C. Kiefer and T. P. Singh have developed a semi classical quantum gravitation from WheelerDeWitt‘s equation of quantum gravitation (ref) and applied this to the Friedmann universe [9-12]. For the motion of matter in this universe, a corrected Schrödinger equation of the following type is given:
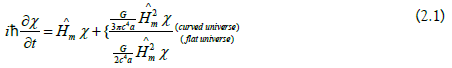
From this fundamental equation, therefore, we derive a non-linear semi classical Hamiltonian of the following structure for the motion of matter in the flat Friedmann universe.

or also, with the scale factor a 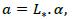

wherein is 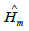 the Hamiltonian of the matter in the Minkowski space and
the Hamiltonian of the matter in the Minkowski space and
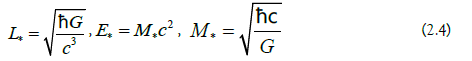
are the Planck-length, Planck-energy and the Planck-mass
Note: In Dirac’s theory, an analogue procedure leads to a semi classical Hamiltonian that is similar to the above gravitative case [13]:
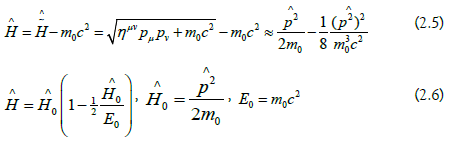
The correction term in (2.6) has the same structure as that in (2.3), but with a negative sign.
Application to the photon gas
Let us now consider an ensemble of harmonic oscillators in the heating bath having a temperature T (Einstein‘s photon model), and determine the mean energy ε of a photon therein. Let us use for that the canonical partition with the one-particle partition sum Z and the Hamiltonian Hˆ in the flat Friedmann universe from (2.3)


As the λ term is a sufficiently small correction term only, we can readily note
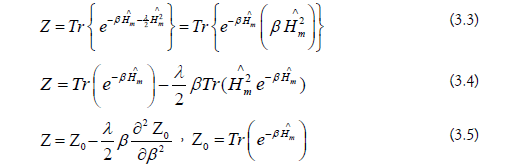
The mean one-particle energy 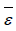 then, as we know, results from
then, as we know, results from

Z0, however, is the one-particle partition sum of the Planck partition in the flat Minkowski space

so that, from (3.5), (3.6) and (3.7), it follows that
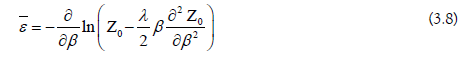
Our interest is focused on the correction of Planck´s radiation law at very high temperatures kT» ħω or βε« 1. For that case we obtain, with (3.7) and (3.8),
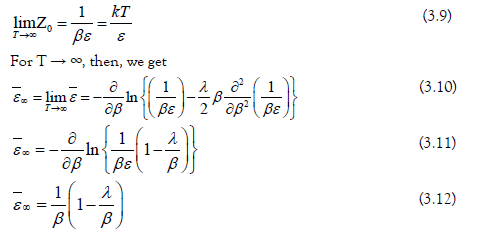
With (3.1) and (3.2), therefore, we obtain
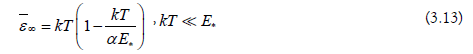
The occurrence of the parameter 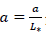 points to the influence of the Friedmann universe. We recognize that the number of classical degrees of freedom per particle deviates from 2, although this
points to the influence of the Friedmann universe. We recognize that the number of classical degrees of freedom per particle deviates from 2, although this 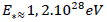 correction, due to the magnitude of the Planck energy is extremely little.
correction, due to the magnitude of the Planck energy is extremely little.
A value for α
Can we in (2.3) set a value forα? In Ref we established an approach to a modified Planck’s radiation law, which we developed in an imitation of Einstein’s well-known laser model [5, 14]. The modified Planck formula, which was based also on statistical considerations, reads as follows:

For temperaturesT →∞ this converts to
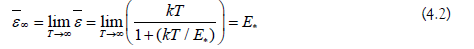

If we now compare (4.3) with our result (3.13) for the Friedmann universe, we can readily conclude that α =1 and also, therefore, from (2.3), that 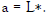 This is well in agreement with the ground state of a quantized universe. A quantization of the Friedmann cosmos provides namely a discretization of the cosmic scale factor and the energy content of the cosmos,
This is well in agreement with the ground state of a quantized universe. A quantization of the Friedmann cosmos provides namely a discretization of the cosmic scale factor and the energy content of the cosmos,
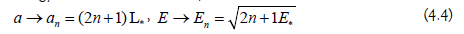
how we can find in [1,15,16]. With n =1 we read off, for ground state length and ground state energy, respectively, the values 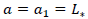 1 and
1 and 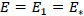 such that α =1 seems to be a reasonable value. According to formula (4.3), however, corrections to the classical Rayleigh-Jeans behavior
such that α =1 seems to be a reasonable value. According to formula (4.3), however, corrections to the classical Rayleigh-Jeans behavior 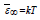 and, thus, to the classical equipartition theorem
and, thus, to the classical equipartition theorem 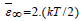 pro photon, will not appear before the temperatures come close to the Planck temperature
pro photon, will not appear before the temperatures come close to the Planck temperature 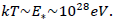 Such temperatures will at best appear at a cosmologically short time after the big bang.
Such temperatures will at best appear at a cosmologically short time after the big bang.
Conclusion
We applied the semiclassical fundamental equation of quantum gravitation, derived from the Wheeler-DeWitt equation by C. Kiefer, to the electromagnetic radiation in a flat Friedmann universe. We used the method of canonical partition and the state function for the ideal photon gas to determine the mean energy 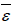 a photon. For very high temperatures (but still kT« E*), there is a deviation from the classical behavior, which now took the form
a photon. For very high temperatures (but still kT« E*), there is a deviation from the classical behavior, which now took the form 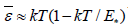 being influenced by the quantity of the Planck energy
being influenced by the quantity of the Planck energy 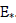
References
- Collier R. Planck's Radiation Law in the Quantized Universe. ArXiv. 2011.[Googlescholar] [Crossref]
- Tawfik A and Diab A. Generalized uncertainty principle: Approaches and applications. International Journal of Modern Physics D. 2014; 23(12):1430025.[Googlescholar] [Crossref]
- Alberto P, Das S and Vagenas EC. Relativistic particle in a three-dimensional box. Physics Letters A. 2011; 375(12):1436-40.[Googlescholar] [Crossref]
- Deb S, Das S and Vagenas EC. Discreteness of space from GUP in a weak gravitational field. Physics Letters B. 2016; 755:17-23.[Googlescholar] [Crossref]
- Das S, Pramanik S and Ghosh S. Effects of a maximal energy scale in thermodynamics for photon gas and construction of path integral. SIGMA. 2014; 10:104.[Googlescholar] [Crossref]
- Zhang X, Shao L and Ma BQ. Photon gas thermodynamics in doubly special relativity. Astroparticle Physics. 2011; 34(11):840-5.[Googlescholar] [Crossref]
- Maziashvili M. Corrections to the black body radiation due to minimum-length deformed quantum mechanics. Physics Letters B. 2011; 705(5):521-8.[Googlescholar] [Crossref]
- Soares I, Turcati R and Duarte SB. Thermodynamics of Blackbody Radiation in Nonlinear Electrodynamics. ArXiv. 2023.[Googlescholar] [Crossref]
- Kiefer C. The semiclassical approximation to quantum gravity. Conference paper, Springer 2005: 170-212.[Googlescholar] [Crossref]
- Kiefer C, Singh TP. Quantum gravitational corrections to the functional Schrödinger equation. Physical Review D. 1991; 44(4):1067.[Googlescholar] [Crossref]
- Chataignier L. Gauge fixing and the semiclassical interpretation of quantum cosmology. Journal of Natural Research A. 2019; 74(12):1069-98.[Googlescholar] [Crossref]
- Sriramkumar L. Limits on the Validity of the Semiclassical Theory—A Minisuperspace Example. International Journal of Modern Physics D. 1997; 6(03):363-75.[Googlescholar] [Crossref]
- Franz Schwabl. Quantum Mechanics. Springer 2000: 188.
- D. Meschede, Gertsen Physik, Springer2002: 580.
- Peleg Y. Quantum dust black holes. ArXiv. 1993.[Googlescholar] [Crossref]
- Garay LJ. Quantum gravity and minimum length. International Journal of Modern Physics A. 1995; 10(02):145-65.[Googlescholar] [Crossref]





