Two-Player Repeated Game: Nash Equilibrium's and Optimal Exit Time

Received: 25-Oct-2021 Accepted Date: Nov 09, 2021; Published: 28-Feb-2023

Citation: Habibi R. Two-Player Repeated Game: Nash Equilibriums and Optimal Exit Time. J Pur Appl Math. 2021; 5(6):89:88.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

This paper is concerned with three typical issues about two-player repeated games. The first question regards the convergence of applied strategy to Nash equilibrium (NE) and corresponding rate of convergence. The second question asks about the optimal exit time for each player. In the third question, it is asked if the pure NE maximizes the mixed NE joint distribution. A Gibbs type sampling is proposed and the above mentioned issues are answered using the sampling method. Finally, concluding remarks are given.

Keywords

Gibbs sampling; Mixed NE; Optimal exit time; Repeated game; Strategy

Introduction

Consider a two-player game with utility functions 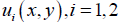, of player 1 and 2, respectively, where, x and y are profits of players 1, 2. Throughout the current paper, it is assumed that x and y are realizations of random variables X,Y with the joint distribution F_X,Y and the marginal distributions, F_X,F_Y respectively. Notations f_X,f_Y stand for density functions (is exist) for continuous X,Y, or the probability mass functions of them in discrete one case. For both cases, the term density is applied.

Also, the notation 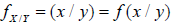denotes the conditional density (if exists) of x given y.

Throughout the current paper, terms “distribution” and “density” are used, interchangeably. According to the game theory literatures, the mixed distribution of Y is a F_Y such that the quantity 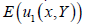, defined by

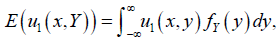
is independent of x, i.e. the first player is indifference with respect to x. (Here, the mixed distribution in the sense of game theory is meant and it is not related to the mixed distributions of statistics).

The above expectation is taken with respect to the family of marginal densities of Y.

That is, the marginal density is found (across the family of densities) which makes the first player indifference.

In the simultaneous game manner, both players’ find their mixed distributions, and consequently, take samples from them, concurrently.

However, in a sequential game version, players of game play consecutive, so, it is rational to consider conditional densities f (x | y) and f ( y | x) , as mixed distributions of both players. Thus, f ( y | x) is chosen such that

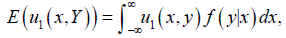
is independent of argument x. In a sequential game setting, time is important because of sequential and repeated structures of the game. Thus, the subscript t is added to notations of variables. Indeed, in a repeated sequential game, at t -th stage of game, the first player observing y _t−1 of his opponent and knowing x_t−1, then, selects the sample x_t from .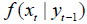

The similar act is done by the second player. As soon as, the number of sampling (number of repetitions of repeated game) increases, the sequential samples from conditional distributions constitutes a two-dimensional Markov chain, similar phenomenon happens in Gibbs-sampling technique which is referred as “Gibbs-type sampling”. Following Gelfand and Smith (1990), the ultimate samples come from the Markov chain stationary distributions of X,Y. For more details, see Casella and George (1992) and references therein.

This sequential sampling manner and stationary distributions are used to answer to three typical questions frequently asked about the repeated games. The above discussion is revisited in the wallet game, as follows:

Example 1. Following Casella and George (1992) part 3, consider a bivariate Bernoulli random vector distributed as

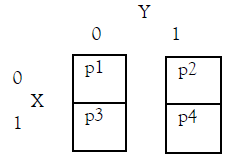
and suppose that the payoff matrix of a two-player game is defined as follows

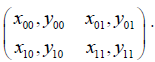
Here, the conditional probabilities matrix are given by

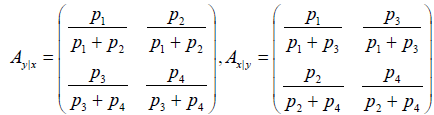
From the Nash equilibrium, it is seen that,

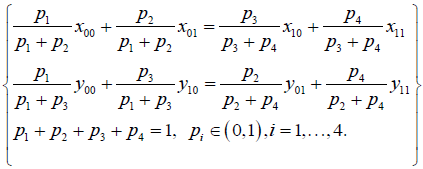
As soon as, a one-shot game is played for a given number of repetitions (such as the poker game), the repeated game setting is born.

Here, the current actions of each player have effects on himself and his opponent future actions. Throughout a specific repeated game, each player learns how to play optimal, see Kaniovski and Young (1995) and references therein. Repeated games broadly are divided into two finite and infinite classes. Finite games are solved by backwards induction technique but infinite games cannot be solved by it.

Instead, players take a strategy such as grim trigger or tit for tat in the front of opponent behavior.

As follows, three typical issues (i) − (iii) of repeated games are proposed and they are answered in the next sections throughout the

Gibbs-type sampling.

(i) Although, there are many strong techniques such as folk theorem to find the sub-perfect NE in a repeated game (see Mailath and

Samuelson, 2006), however, a good question is: which strategies converges to NE and what is the rate (speed) of convergence? That is, after how many stages the NE’s will be appeared? Indeed, if all players are infinitely rational, they will choose the NE (pure NE if it exists, if not, the mixed NE). However, this not true if they are bounded rationality or there exist some imperfect information in each stage of game.

These conditions exist in a repeated stochastic game.

(ii) Repeated games, in both finite and infinite formats, have been received considerable attentions via a huge studies exist in the literatures.

However, choosing between finite or infinite types depends on how long each player is interested to repeat the stage games.

Therefore, another important problem for each player of a repeated game is: what is the optimal time for exit of game?

This problem can be formulated as an optimal stopping problem.

Although, the learning process in the repeated games are well studied in the literatures in famous games such as factious and Bayesian games, however, the optimal exit (stopping) strategies of repeated game seems is less considered. Indeed, this problem can be viewed as game theoretic extension of the optimal stopping strategies. For example, Tijms (2012) applied the optimal stopping technique and used backward induction dynamic programming method for solving stochastic game proposed in a dice game format.

(iii) Choosing between pure (if exist) and mixed NE’s is too important. By checking famous games such as repeated prisoner’s dilemma or chicken games, one can see that the pure NE maximizes the mixed NE joint distribution. It is interested to know is it true for all repeated games?

The rest of paper is organized as follows. In section 2, three issues (i), (ii) and (iii) are studied using the Gibbs-type sampling method. First, following Yao (1984) setting for change point analysis and because of curiosity arguments, a stochastic strategy is chosen for movement of both players and it is searched that under which conditions they lead to NE and what is the rate of convergence to NE? Next, the optimal exit time of repeated game for each player is studied. Applications in option pricing game is studied. Then, it is checked that the pure NE maximizes the mixed NE. In section 3, the Gibbs sampling type is revisited in exchange rate and option pricing. Finally, concluding remarks are given in section 4.

Issues of Repeated Game

Here, three theoretical issues (i), (ii) and (iii) about repeated games, proposed in Introduction, is answered using the

Gibbs-type sampling approach.

(i) Convergence to NE. It is too important to know that under which conditions the players lead to NE and what is the rate of convergence?

This question is proposed throughout a type of stochastic game as follows. Consider a two-player (called player 1,2) game with action profile (states) {0,1} and bi-matrix payoff 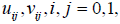as follows

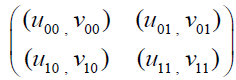
Players 1, 2 start the game by choosing the random states 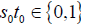where they are mutually independent and have initial distributions 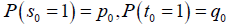. As the game is repeated, then following Yao (1984), next states (actions) 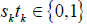are chosen by players 1, 2, respectively, as follows:

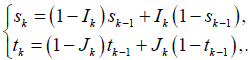
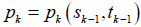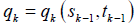Here, i_k j_k are two independent binary random variables at which the conditional transition probabilities of players 1, 2, i.e., and for k-th shot game, k ≥1, are given as follows

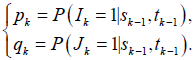
Questions are under which conditions on 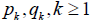the selected stochastic strategies converge to NE (in pure or mixed sense) and after how many stages (steps) players converge to the NE (what is the rate of convergence)? The Gibbs-type sampling approach answers this question.

(ii) Optimal exit time. This sub-section studies the optimal exit time of a two-player game. To this end, consider a two player repeated game at which their utilities at t-th shot play are 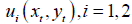. It is interested to find equilibrium optimal stopping time 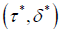at which 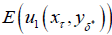is maximized at 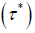and 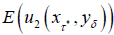is maximized at 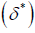. Indeed, 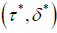is the best response of player 1, 2, respectively.

Again, the Gibbs-type sampling approach answers this question.

(iii) Mixed NE maximize. Here, it is shown that pure NE maximizes the mixed NE. To this end, as a motivating example,

consider the following prisoner’s dilemma with action profile {a,b} and bimatrix payoff

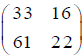
It is seen that the pure NE is joint (b,b) . Also, it is clear that the mixed strategies for both players is 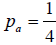. and .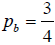

It is seen that the pure NE is the most probable cell according to the mixed strategies. One can see that the same problem occurs in the battle of sexes and chicken game. These examples motivate researchers to check the above hypothesis as a mathematical fact.

To this end, suppose that 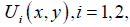, are utilities functions of players 1 and 2, respectively.

The mixed distributions for X and Y are ones that

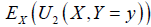and 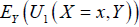are indifference with respect to X,Y, respectively.

In this section, it is interested to show that the joint equilibrium distribution (X,Y) is maximized at pure NE (if exists).

Gibbs Sampling

As follows, the above Gibbs-sampling ideas are applied to some two-player games, including exchange rate and gam theoretical aspects of option pricing.

Exchange rate game. In a given market such as foreign exchange market, the behavior of large investors, say institutional investors, can move price since they are price maker, see Villena and Reus (2016). Existence of such participants in markets versus of atomic investor’s creates a strategic environment at which main economic assumptions like perfect competition and symmetric information do not hold. Thus, the main tool for analyzing these situations is the game theory.

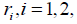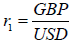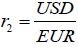Here, following Villena and Reus (2016), and considering a foreign exchange market, suppose that two main players 1,2 exist where each of them determines the level of the exchange rate , respectively, say and . Therefore, the product r₁r₂, itself, is the 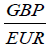exchange rate.

However, if the market price (actual price) of the last exchange rate r₃ does not equal to the product of r₁r₂, this phenomena makes the triangular arbitrage opportunity. In this situation, both large traders try to optimize their utility functions throughout available opportunity.

Suppose that both players have exponential utility functions with positive risk aversion constants 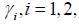i.e., their utilities are given by

.

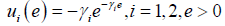Indeed, their expected benefits throughout the possible arbitrage opportunity are given by

.

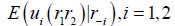Here, r_-1=r₂, if i=1, and it is r₁ if i=2.

Notice that 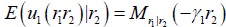, is the moment generating function (if exists) of r₁ given r₂. The quantity 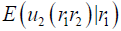is defined, similarly.

To compute the utility functions of both players, conditional distributions of r_2t given r_1t and its reverse are needed.

There are many approaches to this end and model specification. For example, for distribution of r_2t given r_1t, a dynamic regression model as 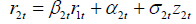, is considered where Z_2t is a sequence of independent normally N(0,1) distributed random variables.

However, to compute the mixing conditional densities, the interceptcorrected versions of variables (and therefore, utility functions of players 1, 2) are defined as

,

,

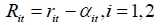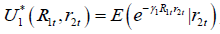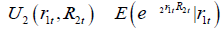, respectively.

The aim of changing format of utilities functions and indeed removing the term of intercept a_it, is to obtain the mixing conditional densities, computationally, easily.

In practice, to remove intercept term a_it, it is possible to consider centralized format of where is the sample mean of i-th returns of -th exchange rates for a pre-determined sample size n.

To compute the utility function, for example, of the second player, i.e., U₂, notice that the term a_2t is removed from regression equation

and assuming a time varying structure for σ_2t, then, it is seen that 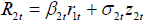. Thus, R_2t given r_1t has normal distribution

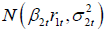
Thus, .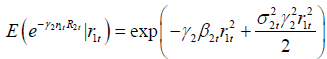

To make sure that the above quantity is independent of r_1t, it is enough to assume that 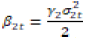. Thus, the mixing conditional distribution of R_2t given r_1t is given by .

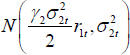Replacing index 1 with 2 and vice versa, then the mixed conditional distribution 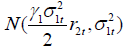for distribution of R_1t given R_2t is obtained. The following proposition covers the above discussion; hence, its proof is omitted.

Proposition 1. Considering utility functions 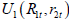and 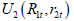for players 1, 2, respectively, and the intercept-corrected rates 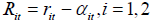, and assuming dynamic equations 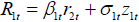and 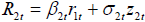, then the mixing (indifference) conditional distributions R_1t given r_2t and R_2t given r_1t are given by

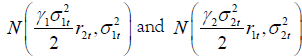, respectively.

Some remarks. Hereafter, some remarks are given.

Remark 1. For a sequential game setting, at t-th stage of mentioned repeated game, each player considers the selected sample of his opponent has been derived at stage (t-1)-th and therefore the samples R_1t, R_2t are drawn from 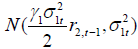and 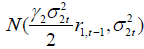distributions, respectively.

Remark 2. The model specification is selected based on empirical intuitions obtained in Example 1 (see below) and some other results obtained from the search among the literature review. Indeed, there are many approaches to model the time varying pattern of β_2t, α_2t.

Here, they may be modeled as random walk structures:

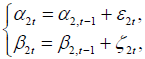where 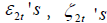are two sequences of random variables which are mutually independent and normally distributed as 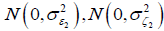, respectively.

Here, σ²_2t may be formulated as a time varying moving average/GARCH series or may be estimated via the Morgan’s (1996) Risk-Metrics approach.

The above model may be considered as a state space model such that the regression equation is measurement equation and dynamics of β_2t, α_2t and σ²_2t play the role of state equations. Replacing index 1 with 2 and vice-versa the dynamics of β_1t α_1t and σ²_2t are found.

Remark 3. Summarizing the above discussions, and re-writing all results in non-centralized rates, it is seen that the equilibrium dynamic regression models are given by 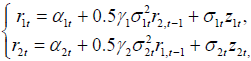where α_it ’s have random walk structures and it σ are estimated using say GARCH series, as it is stated in the Remark 2.

These dynamic models are referred as practical instruction pattern of equilibrium regression models.

Remark 4. If the intercept is not removed, then, following an approach of Proposition 1, it is seen that

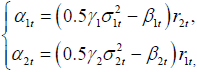
which leads to the equilibrium dynamics

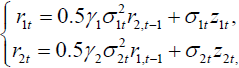
Example 2. Consider EUR/USD (r_1t) and USD/GBP (r_2t) exchange rates for period of study 18-Sep.-2019 to 16-Oct.-2020, including 283 observations taken from www.investing.com site. Here, the rolling (over rolling window with length of 20) least square estimates of α_2t, β_2t are plotted as follows (Figures 1 and 2).

Figure 1: Rolling least square estimates of β_2t.

Figure 2: Rolling least square estimates of α_2t.

These plots suggest a random walk pattern in α_2t, β_2t, because of instability if the mean, visually.

Therefore, the first differences of them are plotted as follows (Figures 3strong> and 4strong>), which are clearly stable processes in mean.

Figure 3: First difference of estimates of β_2t.

Figure 4: First difference of estimates of α_2t.

As well as, the plots of β_2t against β_2,t-1 and α_2t against α_2,t-1, are plotted in (Figure 5a-5bstrong>) respectively.

Figure 5(a): β_2t vs. β_2,t−1.

Figure 5(b): α_2t vs. α_2,t−1.

These plots suggest the use of random walk structure for α_2t, β_2t, strongly.

The figure of moving average estimate (throughout a window by length 10) of σ²_2t is plotted in (Figure 6).

Figure 6: Mowing average estimate of σ²_2t.

Clearly, the volatility clustering (as indicator for existence of GARCH effects) is seen. Fitting a Risk-Metrics dynamic, it is seen that 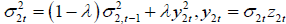, where λ = 0.19 .

Also, it is easy to see that the standard deviations of innovations ε_2t and ζ_2t are 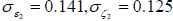, respectively.

Applications in pricing. This sub-section studies for game theoretical aspects of option pricing formulas.

To this end, consider a financial derivative f which its value at the maturity T depends on the values of two independent financial assets s¹, s², for example the Margrabe’s formula, see Rouah and Vainberg (2007).

Here, the Margrabe’s option (as a game between holder and writer of option) is revisited from the wallet game point of view (which this approach is not studied before, and it is useful to run the Gibbs-type sampling method).

First, to review the wallet game, consider the following example. Interested readers are referred to the Carroll et al. (2006) and Ferguson (2006).

Suppose that S¹_T comes from distribution F and S²_T comes from distribution G and S¹_T, S²_T are independent, statistically.

Then, the holder of option receives random amount

.

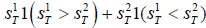where 1(a < b) is one if (a < b) and zero if (a > b) . For simplicity let 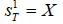and .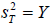

Notice that the expected profit of holder (value) of this game, following the notation of Ferguson (2006), is

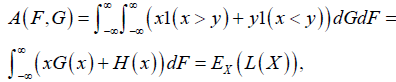where .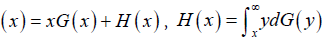

Then, A(F,G) may be approximated by the direct use of Monte Carlo simulation.

Also, notice that 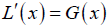and 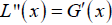is the density function of Y.

The Taylor expansion leads to

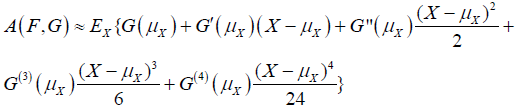
where G(i)is the i-th derivative of G.

Therefore, 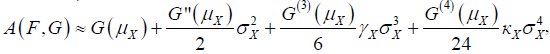At which, γ_X, k_X are skew and kurtosis measures of X. For example, when, Y comes from exponential distribution with parameter one, then,

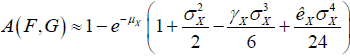
It is seen that, the value of game depends on distributions F and G, via their forth central moments.

Hereafter, the Gibbs-sampling method is proposed.

To this end, notice that the price off at time t, when S²_T are assumed fixed is 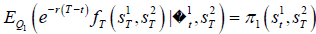, where f¹_t is the information set of the first financial asset s¹ up to time t, and Q₁ is the risk-neutral probability measure of asset 1.

Also, the price of f, assuming S¹_T is kept fixed, is

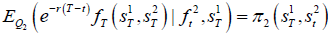
Considering equations set 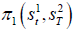, , 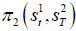a game is defined between asset 1 and 2.

Again, the optimal stopping method may be applied to solve the problem.

Conclusion

The Gibbs-type sampling method is applied to answer some questions about the repeated games, e.g., convergence to NE and its rate of convergence, optimal exit time for a repeated game and the maximizing property of mixed NE.

This type of sampling may be applied to the option pricing and exchange rate games.

REFERENCES

1. Carroll MT, Jones MA, Rykken EK. The wallet paradox revisited. Math Mag 2001,74:378-83.
2. Casella G, George EI. Explaining the Gibbs sampler. Amer Statist 1992, 46:167-74.
3. Ferguson TS, Hardwick JP. Optimal stopping and applications. J Appl Probab 1989,26:304-13.
4. Gelfand AE, Smith AF. Sampling-based approaches to calculating marginal densities. J Am Stat Assoc 1990, 85:398-409.
5. Jank W. Implementing and diagnosing the stochastic approximation EM algorithm. J Comput Graph Stat 2006, 15:803-29.
6. Kaniovski YM, Young HP. Learning dynamics in games with stochastic perturbations. GEB. 1995,11:330-63.
7. Mailath GJ, Samuelson L. Repeated games and reputations: long-run relationships. Oup 2006.
8. Morgan JP. Creditmetrics-technical document. JP Morgan, New York, USA 1997.
9. Rouah FD, Vainberg G. Option pricing models and volatility using Excel-VBA. JWS; 2007.
10. Tijms H. Stochastic games and dynamic programming. Asia Pac Math Newsl 2012, 2:6-10.
11. Villena MJ, Reus L. On the strategic behavior of large investors: A meanvariance portfolio approach Eur J Oper Res 2016, 254:679-88.
12. Yao YC. Estimation of a noisy discrete-time step function: Bayes and empirical Bayes approaches. Ann Stat 1984,10: 1434-47.