A dynamic comprehensive mathematical model for Malthusian trap based elimination principles
Received: 13-Jan-2023, Manuscript No. puljpam-23-6048; Editor assigned: 14-Jan-2023, Pre QC No. puljpam-23-6048 (PQ); Accepted Date: Jan 20, 2023; Reviewed: 16-Jan-2023 QC No. puljpam-23-6048 (Q); Revised: 17-Jan-2023, Manuscript No. puljpam-23-6048 (R); Published: 30-Jan-2023, DOI: 10.37532/2752-8081.23.7(1).23-31.
Citation: Ji Y, Ji M. A dynamic comprehensive mathematical model for Malthusian-trap-based elimination principles. J Pure Appl Math. 2023; 7(1):23-31
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
The Malthusian Trap is a mechanism that describes how population growth suppresses the average income growth in the pre-industrial human history. Studies of the pre-industrial world demonstrated the staggering is worldwide. From the original Malthusian literature, “The perpetual tendency in the race of man to increase beyond the means of subsistence is one of the general laws of animated nature which we can have no reason to expect will change.”, the tendency to “increase beyond the means of subsistence” is an axiom of the Malthusian Trap mechanism. The tendency to “increase beyond the means of subsistence” can also be understand as increase the birth rate as high as possible. On the other hand, the birth rate is observed to be decreasing drastically in modern society. The Demographic transition theory demonstrate this transition from high-birth-high-death to low-birthlow-death over course of economic development. This paper developed a comprehensive mathematical model that tries explaining the high birth tendency in term of natural selection and the transition from high-birth-high-death states to low-birth-low death states in term of whether or not natural selection functions. In the model, three fundamental elimination processes are demonstrated.1) The Low-Average-and-High-Birth-Rate elimination; 2) the High-QuotaElimination based on extra resource; and 3) the High-Quota-Elimination based pure resource distribution. It is also demonstrated that how phenotypes co-exist when they are advantage in different elimination mechanism. Whether or not the elimination process function demonstrated two drastically different situations. Under Malthusian trap, the average income decreased as low as possible while birth rate is pushed as high as possible. Out of Malthusian trap, the average income growth rate is pushed high by decreasing birth rate. The model draws a necessary and sufficient condition between the average income stagger and the elimination processes, thus explained the transition from high-birth-high-death to low-birth-low-death based on shutting off elimination processes. Further analysis on the model demonstrated that the average income under Malthusian trap is related to marginal productivity similar to how wage is decided by the marginal productivity.
Keywords
Dynamic comprehensive; Malthusian-trap; High-Quota-Elimination; Perpetual tendency
Introduction
In his book A Farewell to Alms: A Brief Economic History of the World, CLACK demonstrated how birth rate and death rate balance at specific average income [1-5]. However, the book did not explain why people cannot choose to decrease birth rate to increase living standard. In his book, CLACK explained that decreasing birth rate will increase average income, which intuitively suggest that decreasing birth rate is the rational option [6-13]. However, the rational option was not taken. Why did not people choose lower birth rate to increase their living standards under Malthusian Trap? From the original Malthusian literature [1], the answer to the question is “The perpetual tendency in the race of man to increase beyond the means of subsistence is one of the general laws of animated nature which we can have no reason to expect will change.”
The tendency to “increase beyond the means of subsistence” is a fundamental axiom for the Malthusian trap to function. This assumption assumes that the tendency to increase birth rate triumphs the incentive to increase living standard by reducing birth rate.
This paper provides a comprehensive mathematical model that explain why such tendency functions. The tendency exists because of natural selection. The model is based on the definition of average income and the following 6 assumptions:
1. Creatures need resource to reproduce.
2. With unlimited resource, creature can only reproduce as much.
3. The more resource, the more offspring reproduced
4. All creatures eventually die.
5. Creatures need resource to survive.
6. The more resource, the less creature dies.
The model generated three elimination mechanism. Based on the production growth rate, the model predicts two states of complete different behavior. The under Malthusian trap state, happens when there is NOT enough resource production growth, is the situation where three fundamental elimination principles DO function thus have high-birth-high-death balance and staggered low average income. The out-of-Malthusian-trap state, happens when there IS enough resource production growth, is the situation where three fundamental elimination principles do NOT function thus have increasing average income and incentive to decrease birth rate. The three fundamental elimination principles cause the following effect:
1. Creatures gain as much resource as possible.
2. Creatures fight as hard for resource as possible.
3. Creatures increase efficiency in reproduction as much as possible.
The three trends cannot be unified, creatures advantageous in at least one of the trends will co-exist. Creature is not advantageous in any of these trends will get eliminated.
Basic Relation between Resource and Population
Start with the basic definition of average income.

Where in equation 1 P is the total production of resource, N is the population of some creature and A is the average amount of resource for every individual or average income. Take time derivative of equation 1 and apply the standard dot notation for time derivative dA/dt=A and simplify.

In equation 2, further define the population N as sum of three function: an constant initial population N0, the population that born Nb = Nb (t) and the population that died Nd = Nd (t) over the period of time t.

Substitute equation 4 into equation 2

Take the simplification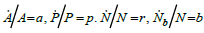 and substitute into equation 5
and substitute into equation 5

In equation 6, p is the percentage economic growth rate or percentage production growth rate; a is the average income percentage growth rate; r is the population percentage growth rate; b and d are percentage birth and death rate [14].
r and R0 from death and birth rate
Based on the death function, the average life span of a population can be calculated as 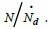 The average life span is the average time takes for a population to replace every individual.
The average life span is the average time takes for a population to replace every individual.

From the average life span, reproduction rate R0 can be calculated as

For fixed death and birth rate b, d and r
The population is under equilibrium when R0=1, r=0 and b=d. The population is growing when R0>1, r>0 and b>d. The population is decreasing when R0<1, r<0 and b

A differential equation system describes average income and population for multiple phenotypes
In equation 6, every term is a percentage change rate. A relation of percentage change rate between population r, resource production/gathering p and average resource a is obtained. Define kth phenotype as sub-population with different death and birth rate function bk=bk(A), dk=dk(A) that are only dependent on the average income A. With this definition of phenotype, the time dependence of the death and birth rate function is treated as 1) introduction of new phenotypes and 2) changes in population proportion of phenotypes. Suppose the population consist of l competing phenotypes and all phenotype shares same average income and resource production.

Where nk=Nk/N gives the proportion of kth phenotype, Σnk=1. Nk gives the population of kth phenotype and N = ΣNk is the total population. 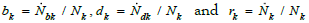 are the percentage birth, death and population change rate for kth phenotype. b=Σnkbk, d=Σnkdk and r=Σnkrk are the percentage birth, death and population change rate for the whole population.
are the percentage birth, death and population change rate for kth phenotype. b=Σnkbk, d=Σnkdk and r=Σnkrk are the percentage birth, death and population change rate for the whole population.
Calculate the time derivative of kth phenotype’s proportion in the whole population.

In equation 11 bk and dk only depends on average resource A, bk=bk(A) and dk = dk(A). The resource production function depend on time and population p=p(N1 ...Nk,t). If the function bk(A), dk(A) and p(N1 ...Nk,t) are specified, the population and average resource development will be fully described by the following system of differential equations.
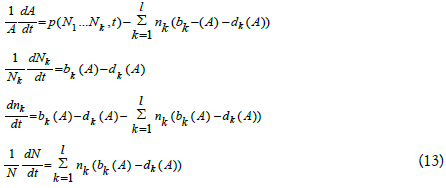
Though, it is hard to obtain exact bk(A)s, dK(A)s and p(N1 ...Nk,t), by determine boundary and general trending of these functions, the general trending of the population and average income can be obtained.
Elimination and inferior-growth
The differential equation system in equation 13 can be used to predict what phenotypes are eliminated. For any phenotype, if equation 13 predicts

then, kth phenotype is eliminated.
One important feature is the differentiation of elimination process and inferior-growth process.
Elimination
Phenotype k is eliminated if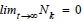
Inferior-growth
Phenotype k have an inferior-growth if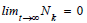
Based on the definition of elimination and inferior-growth:
1. A phenotype is eliminated if rk<0
2. A phenotype is inferior growth if rk
In both cases, the phenotype’s population proportion goes to nk→0. The inferior-growth is a necessary condition for elimination while elimination is sufficient condition for inferior growth. When a phenotype is eliminated, the phenotype will disappear overtime, on the other hand when a phenotype is inferior-growth, the phenotype does not disappear. In case of inferior-growth the phenotype’s proportion in the whole population drop to 0, but there still is a substantial population of the phenotype existing. In case of elimination, the population of the phenotype drops to 0.
Birth rate and death rate balancing mechanism for single phenotype under limited resource
Before dive into the elimination mechanism, first demonstrate the birth rate and death rate balancing mechanism for single phenotype under fixed production P.
Substitute the function of birth rate b(A) and death rate d(A) into equation 6, then the average income exponential change rate a(A) can be solved based on function of production exponential change rate p. At the same time, the population change rate r can be directly solved from b and d. A differential equation system completes describe the population and average income based on birth rate b, death rate d and production change rate p is obtained.

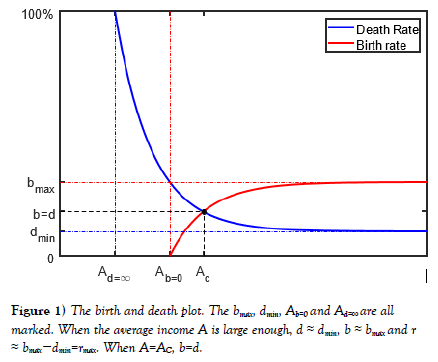
Put the 6 assumptions of birth rate and death rate in mathematical formal way. In term of percentage birth rate b:
1. There exist a no-birth-average-income Ab=0 such that when the average income A is less than the no-birth-average-income A
2. There is a upper bound on the birth rate bmax>0 such that when the average income reaches infinity, the birth rate approaches bmax. (b→bmax as A→∞). (With unlimited resource, creature can only reproduce as much.)
3. The birth b is a monotonic increasing function of average income A. (The more resource, the more offspring reproduced.)
In term of percentage death rate d:
1. There exist a all-death-average-income Ad=∞ such that when the average income A is less than the all-death-average-income A
2. There is a lower bound on the death rate dmin>0 such that when the average income reaches infinity, the death rate approaches dmin. (d→dmin as A→∞). (All Creature eventually die.)
3. The death b is a monotonic decreasing function of average income A. (The more resource, the less creature die.)
From the monotonicity assumption and the boundary of the death and birth rate, the ranges of birth and death rates are d in (dmin, ∞) and b in [0, bmax). Because of basic elimination principle from equation 14, all phenotype with bmax ≤ dmin, will be eliminated Figure 1.
Look at the p = 0 situation, the differential equation becomes

Figure 1 shows a plot the death and birth rate based on these assumptions. Only when the average income A is larger than alldeath- average-income and no-birth-average-income A>Ad=∞, Ab=0, the population survive and give birth. Because the monotonicity of the birth and death rate and the fact that dmin
Fundamental Elimination Mechanism
Even though equation 13 assumed time Independence on bk and dk, time dependency of bk and dk can always be treated as introduction of new phenotypes, which can be understood as mutations. Based on the definition of elimination and general assumption of the birth and death rate bks and dks, rules of elimination can be determined. With these rule of eliminations, one can predict what new phenotype will eliminate old phenotypes. Such a prediction will determine a general direction of evolution. By assuming p=0, three general elimination mechanism is demonstrated.
Low-Average-Income-and-High-Birth-Rate (HAHBE) mechanism
Higher-Birth-Rate Elimination (HBE)
A simple elimination mechanism can be formed with two assumptions: 1) the total population stay constant, 2) all different phenotypes share the same percentage death rate. Consider the simple 2 phenotype case, because the total population is fixed, the total death rate and birth rate is under equilibrium b=d. The two phenotypes have different birth rate b1 and b2 but have the same death rate d. The birth/death rate of the whole population is

Since the death rates of both phenotypes are the same as the full population’s death rate d = d1 = d2, the exponential growth rate for the population of two phenotypes is given by
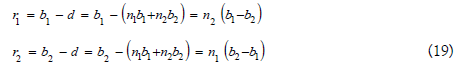
From equation 19, the term n1 and n2 are always positive; the b1−b2 and b2−b1 always have the same value and opposing sign. So, the exponential growth rate of the two phenotypes are always one positive and one negative, where the positive phenotype has greater birth rate and the negative phenotype have lesser birth rate. Equation 19 reviewed the High-Birth-Elimination (HBE) mechanism, where phenotype with greater birth rate will eliminate phenotype with lesser birth. Extending to more than two phenotypes, the phenotype with highest birth rate will eliminate all other phenotypes. The HBE is the reason for the Malthusian “increase beyond the means of subsistence” tendency and the reason why there is no choice in lower birth rate to increase living standard. Choosing lower birth rate leads to elimination.
Based on the HBE, elimination time can be estimated based on the birth rate difference. Rearrange equation 19 to obtain differential equations on n1 and n2, solve the differential equations and calculated time needed for the population proportion to change from ni1 and ni2 to nf1 and nf2.
Time T needed for two phenotypes to vary from initial proportion of (99%, 1%) to final proportion (1%, 99%), based on birth rate difference Δb=|b1−b2| is given by

From equation 20, two phenotypes with 1% birth rate difference takes 919 years for the population proportion to change from 99% to 1% and 1% to 99%; 2% takes 459.5 years; 0.1% takes 9190 years. Based on the estimation, the HBE function on time scale of hundreds of years to tens of thousands of years.
Low-Average-Income Elimination (LAE)
The HBE reviews some aspect of the direction of evolution, however there is a fundamental flaw with the logic. A hidden assumption in the logic is that the death rate does not affect birth rate. Because of the hidden assumption, the HBE pushes birth rate to infinity. By relating the average income (in term of resource or monetary currency) to the birth and death rate (bk=bk(A) and dk=dk(A)), the birth rate is limited by the death rate. A more sophisticated elimination mechanism based on average income is obtained.
Suppose there are two different phenotypes with different death and birth functions. Continue with the n1 and n2 notation from equation 18. n1=N1/N and n2=N2/N are proportion of the two phenotypes in the whole population. N1+N2=N gives the total population of the two phenotypes. The overall death and birth rate are given by

Substitute into equation 6

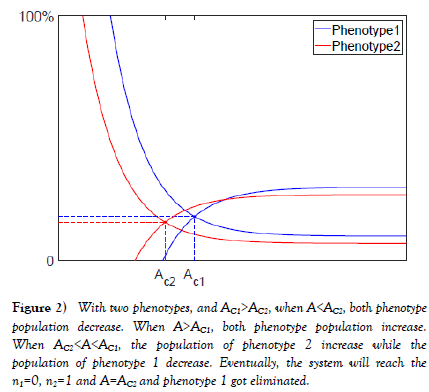
Figure 2 shows the situation with two phenotypes. The two phenotypes have two different critical average income AC1 and AC2 with AC1>AC2. For constant total production P and p=0, a=−n1r1−n2r2. The population of two phenotypes and the average changes according to the following trend:
Figure 2: With two phenotypes, and AC1>AC2, when A<AC2, both phenotype population decrease. When A>AC1, both phenotype population increase. When AC2<A<AC1, the population of phenotype 2 increase while the population of phenotype 1 decrease. Eventually, the system will reach the n1=0, n2=1 and A=AC2 and phenotype 1 got eliminated.
1. When A<AC2<AC1, r1 and r2<0 with a>0. Both phenotype’s population decrease while the average income increase.
2. When A>AC1>AC2, r1 and r2>0 with a<0. Both phenotype’s population increase while the average income decrease.
3. When AC2< A<AC1, r1<0 and r2>0, a=−n1r1−n2r2. The trend of average income change cannot be determined, but the population of phenotype 1 increases while the population of phenotype 2 decreases.
4. At A=AC1, r1=0, r2>0. Unless n2=0, a<0. Unless phenotype 2 have 0 population ratio, the average income decreases and enter the AC2<A<AC1 region. The population of phenotype 2 is increasing while population of phenotype 1 stays same.
5. At A=AC2, r2=0, r1<0. a>0 when n2>0 and a=0 when n2=0. If phenotype 1 have 0 population, average income reaches equilibrium. If there is a non-zero population for phenotype 1, the average income will increase and enter the A=AC2, while population of phenotype 2 stays same and population of phenotype 1 decrease.
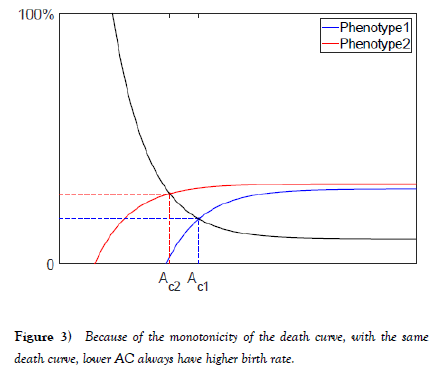
Base on the analysis of the trend of A’s and N’s dependency and on A, n1 and n2, for any initial Ai, n1i, n2i, A first enter the region [A1, A2] if A does not start in the region and then approaches AC2. The population N approaches N=P/AC2. The population proportion n1, n2 approach n2=1 and n1=0. The population of two phenotype approach N2=P/AC2 and N1=0. The trend indicates that phenotype 1 will be eliminated because of the higher critical average income Figure 3.
The analysis demonstrated the lower-average-elimination-mechanism (LAE). This mechanism can be easily extended to multiple phenotype case, the phenotype with lowest critical average income ACmin will eliminate all other phenotypes. Contradict to the instinctive of economical prediction that the economics system always develop toward higher average income, the LAE will push the average income lower. Whenever a now phenotype with new lowest average income ACmin appear, it will eliminate the original population and dominate.
With the LAE, the HBE can be re-examined. Since the mechanism of LAE does not require a constant population size, only keep the assumption of 2 phenotypes share the same death function. Figure 3 shows how HBE function under LAE. When the two phenotypes share the same death rate curve, the lower AC always have higher birth rate, because of the monotonicity of the death rate curve. If the birth rate curve is considered to be the maximum birth rate of a phenotype at certain average income level A, the HBE predict that the phenotype exhausts their resource to reproduce. The HBE eliminate all phenotypes does not exhaust their resource to reproduce.
At this point, the LAE and HBE are unified under the same mechanism. The HBE is just the LAE with same death rate function. It is adequate to combine the two-elimination-mechanism into one Low-Average-Income-and-High-Birthrate (LAHBE) elimination. Though, HBE does have extra importance. Because of HBE, it is important to identify that the birth function in the analysis only based on the physiological limits and exclude the factor of individuals’ choice. The choice of not exhaust their resource and given birth to less offspring will eliminated the individuals who made such choice. Only the individuals exhaust their resource will survive. Thus, the birth function under the analysis is independent of personal choice and only depends on the physiological limits.
If the average income can be equated with living standards, the LAE indicate a constant trend in decreasing the living standards. The LAE will push the living standard or living conditions of any creature as low as possible in exchange of producing as much off-spring as possible. The LAE is a different way of understanding the Malthusian trap. The average income staggering effect of Malthusian trap is caused by the LAE. Since the LAE is pushing the average income as low as possible.
High Quota Elimination
Until this point, the elimination does not consider effect of resource distribution.
Define a normalized income distribution function f such that

The population proportion, average income birth rate and death rate between income I1 and I2 is given by

Then for an arbitrary income level Iarb, the population growth rate r above and below Iarb is given by

For a population under equilibrium naboverabove+nbelowrbelow=0. The population have income above Iarb is constantly growing while the population have income below Iarb is constantly decreasing. The exact number of population growing/decreasing is the same. The population lost below Iarb is exactly made up by the population gain from above Iarb.
Now, in two phenotypes competing situation, suppose the two phenotypes share the same birth rate and death rate function. The difference is that there is a mechanism forcing one of the phenotypes always have income cap Ic. The phenotype with the income cap Ic will constantly loosing population and eventually got eliminated.
This is a very generalized High-Quota-Elimination (HQE) mechanism. The HQE is the elimination based on resource gathering and distribution process while the LAHBE is elimination based on resource utilization efficiency.
High Quota Elimination based on gain access to extra resource (HQE1)
There is two intrinsically different mechanisms that could cause difference in average income. In this section, the HQE1 that leads to increase in total production P is analyzed.
Suppose there are two phenotypes with the total production function P=P1+P12, where P12 is the part of resource accessed by both phenotypes while P1 is only accessed by phenotype 1. So that the two phenotype 1 gain access to extra resource. The average income for two phenotypes are:

Suppose the two phenotypes have the same death and birth function, b1=b2, d1=d2 and AC1=AC2=AC. At A2=AC, A1>AC, r1>0 and r2=0. Based on equation 35, with all proportion n1 and n2, there is always A1>A2. When phenotype 2 reaches the critical average income AC, phenotype 1 population is still growing. As the population growing, the average income of the two phenotypes enters the region A2<AC, A1>AC, r1>0 and r2<0, until eventually a new balance reached at A2<AC, A1=AC, r1=0 and r2<0. Over the whole process, the population growth rate of phenotype 2 is always negative, so phenotype 2 is eliminated.
This is the HQE1 based on gain access to extra resource. The mechanism gives an elimination-based incentive to develop new technology, explore new resource and develop ability to access new resource. The eliminate caused by extra resource indicated that progress in production will cause elimination. If gain access to extra resource indicates advance in technology, the HQE1 demonstrated that technology advance will cause elimination.
In the same production function above, if the two phenotypes have different AC1 and AC2, if AC1>AC2, phenotype 2 is eliminate by both LAHBE and HQE. In case of AC1<AC2, two phenotypes will co-exist at
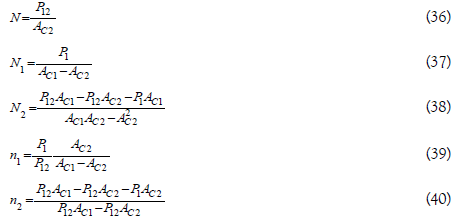
The co-existence of the two phenotypes indicates that the HQE and LAHBE mechanism cannot be unified. When two elimination mechanisms cannot be unified, phenotypes advantageous in one of the elimination mechanisms and disadvantageous in the other elimination mechanism will co-exist at a specific population proportion n1 and n2.
High Quota Elimination based on pure distributional advantage (HEQ2)
The second mechanism that led to HQE2 is based on pure distributional advantage; such advantage will not cause increase in production.
Suppose the two phenotypes share the same production P, and somehow have different average income based on the population proportion of the two phenotypes. The average income of the two phenotype is given by

Define the function ϵ(n1, n2) to be the distribution function. It measures difference in resource distribution between the two phenotypes. In case of just two phenotype, the distribution function ϵ(n1, n2) can be express as only one phenotype’s population proportion. The distribution function ϵ must 1) in range (0,1), 2) concave down and 3) ϵ(1, 0)=ϵ(0, 1)=0.
Apparently, in this case, A1>A2 all the time. If the two phenotypes’ birth and death rate function are the same b1=b2 and d1=d2, phenotype 2 will be eliminated. This is HQE2 based on pure distributional advantage. The difference in average income could come from two causes. 1) A phenotype is more efficient in resource production. The advantageous phenotype is producing resource at a higher efficiency thus chew on the resource of the disadvantageous phenotype. 2) There exists an extra resource redistribution process, which relocate resource produced by the disadvantageous phenotype to the advantageous phenotype.
Apparently HQE2 based on pure distributional advantage cannot be unified with LAHBE and HQE1 based on extra resource. For LAHBE, the two elimination mechanism co-exist at

Where AC1>AC2.
The co-existence of the two HQEs happens at
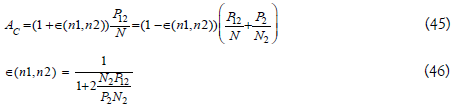
The direction of evolution
Combine all the elimination mechanisms discussed, three general directions of evolution can be derived.
1. Based on HQE1, every creature evolves towards gathering or producing as much resources possible.
2. Based on HQE2, every creature evolves towards gain as much pure distributional advantages possible. This could be achieved through higher production efficiency or ability to fight for resource.
3.Based on LAHBE, every creature evolves towardsincreasing reproduction efficiency by achieve birth-death balance atas low average income as possible. In the process, creature willexhaust all the resource to produce off springs.
The three-trend lead to advantage in the following categories.
1.Ability in gathering new resource.
2.Efficiency in fight for resource.
3.Efficiency in utilizing resource.
Because the three trend cannot be unified, phenotypes are eliminated only when they are not advantageous in any one of these three categories. The phenotypes will co-exist if they take advantage in at least one of the categories.
Malthusian Trap and The Economic Growth
Until this point, all analysis is based on constant production p=0. What would happen if p>0? Malthusian trap describes a situation where income is staggered because economic growth is lower than population growth. Consider situation with economic growth rate p>0. Apparently HQEs can be treated as incentive for positiveproduction growth rate p. The population trend and eliminationprocess can be re-examined.
Malthusian Trap and escaping the Trap
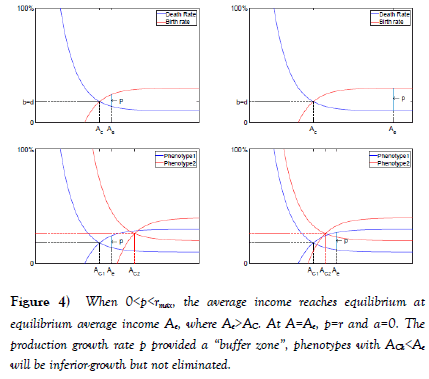
First, define a maximum population growth rate rmax=bmax−dmin. If p>rmax, p>r all the time. From equation 6, a>0 when p>rmax, theaverage income is always increasing, which indicates that eliminationprocesses based on decreasing average income all shut off. Since theMalthusian trap describes a situation with staggered average income, Malthusian trap describe the situations where 0<p< rmax.
Figure 4 showed the situation with 0<p< rmax. Define the equilibrium average income Ae such that at A=Ae, r=p. When A>Ae, r>p and a=p−r<0 the average income decrease. When A<Ae, r<p and a=p−r>0 the average income increase. When A=Ae, r=p and a=r−p=0 the average income stays constant. When 0<p<<rmax, the average income approaches equilibrium average income Ae overtime instead of the critical average income AC, while the population increase at a rate r=p.
In case of multiple phenotypes, the average income will approach phenotype with lowest equilibrium average income Aemin. The phenotype, that have lowest equilibrium average income Aemin, have the population growth rate r=p. Phenotypes with critical average income ACk>Aemin will be eliminated, as they have rk<0. Phenotypes with ACk<Aemin will be inferior-growth, as they have rk≤p. In any case, the population proportion for the phenotype with lowest equilibrium average income Aemin will dominate nemin→1.
Over all, when the production growth rate is constant in the range 0<p<<rmax; the average income approach A=Aemin; the population growth rate approaches r=p; the proportion of the phenotype with minimum equilibrium average income approaches 1; the proportion of phenotype with their critical average income ACk<Aemin approaches 0 but still have a growing population; the proportion of phenotype with their critical average income ACk>Aemin have their population approaches 0 thus get eliminated. The LAHBE still works with a production growth rate 0<p<<rmax. Rather than suppress the critical average income AC, when there is a production growth rate 0<p<<rmax, the mechanism suppresses equilibrium average income Ae. Thus, the HBE still functions with 0<p<<rmax, except when phenotypes’ birth rate difference Δb<p, phenotype with lower birth rate blow will not be eliminated but have inferior-growth. As for HQE, since the LAHBE is functioning, the average is suppressed at Ae, difference in average income Ak would cause growth rate difference and thus cause inferior-growth or elimination. When the economic growth rate is not high enough 0<p<<rmax, increasing economic growth rate p will not start growth in average income, but rather increase the equilibrium average income Ae. Even with production growth, the average income is still staggered.
Based on the analysis of the elimination process, the two major feature of the Malthusian trap (high-birth-high-death balance and staggering average income) are caused by elimination process rather than economic incentives. The LAHBE are forcing high-birth-high-death balance and average income staggering. The HQE1 provides an elimination-based incentive to develop the economy or gain access to new resource. Based on the mechanism for LAHBE, the p<<rmax is necessary and sufficient condition for the LAHBE to function. Because HQE require correlation between income level and population growth rate, low staggered income is the necessary and sufficient condition for HQE to function. Thus, average income staggering is necessary and sufficient condition for elimination process to function.
Out-of malthusian trap
Apparently the escaping the trap happens when p>rmax. From Figure 4, as p→rmax, Ae→∞. When p>rmax, there is no equilibrium average income as the average income is increasing. All elimination processes based on average income decrease (LAHBE) are shut off. The HQE is shut off after the average income A is high enough so that difference in population growth rate r(A) is negligible. As average income increase, the death rate will continue to decrease and eventually reach d=dmin. The life span of population reaches the maximum life span Lmax. Ideally everyone dies because aging. In term of the birth rate b, personal choice on birth become the dominant factor in this regime. Since HBE no longer functions, individuals’ choice in how much offspring they produce will no longer cause elimination. Thus, economic incentives start play major role in reproducing. It is clear from equation 6 that increasing in economic growth rate p will cause increasing in a; and decreasing in birth rate b will cause increasing in a. Decreasing birth rate increases living standards in this region. The idea that decreases birth rate cause increase in average income growth provides economic incentives in decrease birth rate. The the elimination process only requires that eventually b≥dmin, so that phenotype do not self-eliminate. There is not even a process that maintains a high population size. Eventually the population change rate and average income change rate will balance at

Where the average income change rate will be exactly the production growth rate and the birth will match the minimum death rate and the population will eventually balance at some level with mechanism independent of average income variance. The population level will be fully decided by economical mechanisms where the population size is related to the process of maximizing economic growth.
Compare the population trend under Malthusian trap and out of Malthusian trap, the rmax function as a ’phase-changing’ point. With p<rmax, the elimination process are functioning. There is an elimination based ’feed-back-loop’ in increasing birth rate and decreasing average income. Thus, causing the population to grow as fast as possible and decrease the living standard as low as possible. With p>rmax the average income is increasing; the elimination mechanisms are shut off. As the average income start to grow, there is an economical incentive based ’feed-back-loop’ in decreasing birth rate and increasing average income. The two situations will demonstrate great difference in average income and birth rate.
Malthusian trap in terms of marginal production increase
The model could also demonstrate relation between Marginal Production and average income under and out of Malthusian Trap. From the basic a=p−r equation, the following relation can be derived.
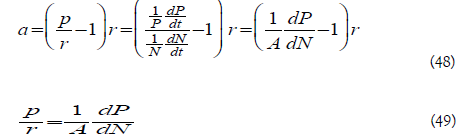
Equation 48 and 49 how the population and production growth rate r and p are related to the marginal production growth increment per person dP/dN. Since under Malthusian Trap, the average income is staggered a=0 and r=p. The marginal production growth increment per person exactly equal to the average income.

Equation 50 implicated that under Malthusian Trap, the average income will reach equilibrium when the average income equates to the marginal production growth increment per person. The average income under Malthusian Trap equal marginal productivity similar to how wage is decided under Marginal Productivity Theory [12].
The escaping of Malthusian trap happens when p>rmax. In terms of equation 49, this indicates that

In the out of Malthusian trap situation, because the population growth cannot keep up with the production growth, the marginal production increment is always larger than the average income. The escaping of the Malthusian Trap happens when the marginal production increment is kept always higher than the average income.
In term of marginal production increment, the ratio 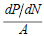 is a
major indication of whether or not the population is under
Malthusian trap. Malthusian trap happens when the fraction
is a
major indication of whether or not the population is under
Malthusian trap. Malthusian trap happens when the fraction 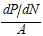 can drop below 1. Escaping the Malthusian trap require that the
fraction
can drop below 1. Escaping the Malthusian trap require that the
fraction 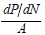 is always kept above 1.
is always kept above 1.
The Effect of Elimination On Human Being
In the paper, it is clearly established that staggered average income is necessary and sufficient condition for all three-elimination process to function. Based on data from CLARK’s book A Farewell to Alms: A Brief Economic History of the World [2], it is demonstrated that the average income increase starts from 1800 with the industrial revolution. This indicates that the elimination process on human being functioned until 1800. From 1800, the average income started to increase in human being, which indicate that we were breaking free from elimination processes. Whether or not elimination process’s function imposes vast difference in living condition. The elimination mechanisms are a major factor must be considered in study of pre-industrial society.
By comparing birth rate under and out of Malthusian Trap. The model predicts a drastic change in birth-rate. Birth rate under Malthusian Trap is driven as high as possible while out of Malthusian Trap birth rate is driven as low as possible. In out of Malthusian Trap situation, an inverse relationship between average income and birth rate can be drawn. Vast amount of data shows such inverse relation [15,16].
Conclusion
Based on simple definition of average income and population, a differential equation system of average income and population development is obtained. The input function for the differential equation system is death rate function dk(A), birth rate function bk(A) and production growth function p(N1 ...Nk,t). Based on 6 assumptions for the death and birth rates functions and the simplification p = 0, three different elimination process are obtained. The LAHBE decrease average income and increase birth rate, leads to increase in reproduction efficiency. The HBE1 based on extra resource leads to creature increase the ability to gain extra resource. The HBE2 based on pure distribution leads to creature increase the ability to fight for resource. It is also demonstrated how these three fundamental elimination processes interact. Co-exist happens when phenotypes show advantage in at least one of these criteria. Elimination happens when phenotype show no advantage in any one of these criteria.
Examine the situation p>0, fundamental differences between the under Malthusian trap p<<rmax and out of Malthusian trap p>rmax are demonstrated. Under Malthusian trap p<<rmax, LAHBE is functioning, the trend of maximizing birth rate and minimizing average income dominates. The birth-death-balance at a high-birthhigh- death situation, population is increasing as production increases while average income stays staggered. A positive economic growth rate rmax>>p>0 will not cause average income growth, but only increase the average income a little bit. Out of Malthusian trap p>rmax provide a situation where average income is increasing, LAHBE are shut off. The economic incentive to decrease birth rate start functioning. The birth-death-balance balances at low-birth-low-death situation. The average increases as the production increase. The exact population size will be decided by other mechanism based on economic incentives.
References
- Malthus R T. An Essay on the Principle of Population. 1872.
- Clark G. A farewell to alms. Princeton University Press. 2008.
- K¨ogel T, Prskawetz A. Agricultural productivity growth and escape from the malthusian trap. J econ growth.2001:6(4);337–57
- Clark G, Cummins N. Urbanization, mortality, and fertility in malthusian England. Am Econ Rev.2009:99(2);242–47
- Lizot J. Population, resources and warfare among the yanomami. Man.1977:497–517
- Allen C R, Bassino P J, Ma D, et al. Wages, prices, and living standards in china, 1738–1925: in comparison with europe, japan, and india. Econ Hist Rev. 2011:64(1);8–38
- J´o´zwiak J, Kotowska E I. Decreasing birth rates in europe: reasons and remedies. Eur View.2008:7(2)225–36
- Marboutin E, Peroux R. Survival pattern of european hare in a decreasing population. J Appl Ecol.1995:809–16
- T. J. Espenshade, J. C. Guzman, and C. F. Westoff, “The surprising global variation in replacement fertility,” Population Research and Policy Review, vol. 22, no. 5, pp. 575–583, 2003.
- Kirk D. Demographic transition theory. Popul stud. 1996:50(3);361–87
- Caldwell C J. Toward a restatement of demographic transition theory. Popul dev rev.1976:321–66.
- Hicks J. The theory of wages. Springer. 1963.
- Scott J. Rational choice theory. Understanding contemporary society: Theories of the present. 2000:129(1);671–85
- Peterson F W E. The role of population in economic growth. Sage Open. 2017:7(4);21
- Kingsland E S, Kingsland E S. Modeling nature. University of Chicago Press.1995.
- Schultz P T. Fertility and income. Understanding poverty. 2006:125–42