A newtonian-vortex cosmology model from solar system to galaxy to large scale structures: Navier-stokes-inspired cosmography

Received: 29-Nov-2017 Accepted Date: Dec 08, 2017; Published: 15-Dec-2017

Citation: Christianto V, Smarandache F. A newtonian-vortex cosmology model from solar system to galaxy to large scale structures: navier-stokes-inspired cosmography. J Mod Appl Phys. 2017;1(1):10-13.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

Some years ago, Matt Visser asked the following interesting questions: How much of modern cosmology is really cosmography? How much of modern cosmology is independent of the Einstein equations? (Independent of the Friedmann equations?) These questions are becoming increasingly germaneas the model’s cosmologists use for the stress-energy content of the universe become increasingly baroque. Therefore, in this paper we will discuss a novel Newtonian cosmology model with vortex, which offers wide implications from solar system, galaxy modeling up to large scale structures of the Universe. The basic starting point is very simple: It has been known for long time that most of the existing cosmology models have singularity problem. Cosmological singularity has been a consequence of excessive symmetry of flow, such as “Hubble’s law.” More realistic one is suggested, based on Newtonian cosmology model but here we include the vortical-rotational effect of the whole Universe. We review an Ermakov-type equation obtained by Nurgaliev, and solve the equation numerically with Mathematica. A potential application is also considered, namely for understanding tornado dynamics using 3D Navier-Stokes equations. It is our hope that the new proposed method can be verified with observations, in order to open new possibilities of more realistic nonlinear cosmology models.

Keywords

Ermakov-type equation; Nonlinear cosmology; Newtonian cosmology; Vortex dynamics, turbulence; Navier-Stokes equations; Spiral galaxy

Introduction

Some years ago, Matt Visser asked the following interesting questions: How much of modern cosmology is really cosmography? How much of modern cosmology is independent of the Einstein equations? (Independent of the Friedmann equations?) These questions are becoming increasingly germane-as the model’s cosmologists use for the stress-energy content of the universe become increasingly baroque [1].

In this regard, academician Isaak Khalatnikov mentioned at the 13^th Marcel Grossman Conference, that Lev Landau suggesting that something is too symmetric in the models yielding singularities, and that this problem is one of the three most important problems of modern physics. The aim of this report is to show that singularities are, indeed, consequences of such an overly “symmetrical approach” in building non-robust (i.e. without structural stability) toy models with singularities. Such models typically apply a synchronous system of reference and “Hubble’s law”, neglecting not-tobe- averaged-out quadratic terms of perturbations (specifically, differentially rotational velocities, vortexes) [2].

Only by accounting the overlooked factors instead of Einstein’s ad hoc introduction of a new entity, which was later declared by him as his “biggest blunder”, can we correctly interpret accelerated cosmological expansion, as well as provide possibility of static solution. The common perception of the observed accelerated expansion is that there is need either in modifying the General Relativity or discover new particles with unusual properties. Both ways are possible depending on what kind of system of reference and corresponding interpretation are chosen, a decision which is usually made depending on the level of “geometrization” [2].

Local rotations (vortices) play a role in radical stabilization of the cosmological singularity in the retrospective extrapolation, making possible a static or steady-state (on the average) Universe or local region. Therefore, Einstein could “permit” the galaxies to rotate instead of postulating a cosmological constant ad hoc in his general-relativistic consideration of a static Universe. Though, it does not necessarily mean that thecosmological constant is not necessary for other arguments [3].

In this paper, more realistic one is suggested, based on Newtonian cosmology model but here we include the vortical-rotational effect of the whole Universe. We review an Ermakov-type equation obtained by Nurgaliev [2,3], and solve the equation numerically with Mathematica 11.

In this paper we will also discuss a novel Newtonian cosmology model with vortex, which offers wide implications from solar system, galaxy modeling up to large scale structures of the Universe.

It is our hope that the new proposed method can be verified with observation data.

A Few Historical Notes

Since long time ago, there were numerous models of the Universe, dating back to Ptolemaic geocentric model, which was subsequently replaced by Nicolas Copernicus discovery. Copernicus model then was brought into fame after Isaac Newton published his book. But other than Newton, there was a model of Universe as a turbulent fluid (hurricane) brought by a French philosopher and mathematician, R. Descartes. But, this model was almost forgotten. Many physicists rejected Descartes’ model because it stood against Newtonian model, but the truth is turbulence model can be expressed in Navier-Stokes equations, and Navier-Stokes equations can be considered as the rigorous formulation of Newtonian laws, especially for fluid dynamics. In other words, we can say that Newtonian turbulence Universe is not in direct contradiction with Newtonian laws. Therefore, in this paper we submit wholeheartedly a proposal that the Universe can be modelled as Newtonian-Vortex based on 3D Navier-Stokes equations. We shall show some implications of this new model in the following sections.

Solar System Model

In this section, we will review the work which was carried out by VC and FS during the past ten years or so. The basic assumption here is that the Solar System’s planetary orbits are quantized. But how do their orbits behave? Do they follow Titius-Bode’s law? Our answer can be summarized as follows: [4-6].

Navier-Stokes equations→superfluid quantized vortices→Bohr’s quantization

Our predictive model based on that scheme has yielded some interesting results which may be comparable with the observed orbits of planetoids beyond Pluto, including what is dubbed as Sedna [7]. And it seems that the proposed model is slightly better compared to Nottale-Schumacher’s gravitational Schrödinger model and also Titius-Bode’s empirical law.

Spiral Galaxy Model

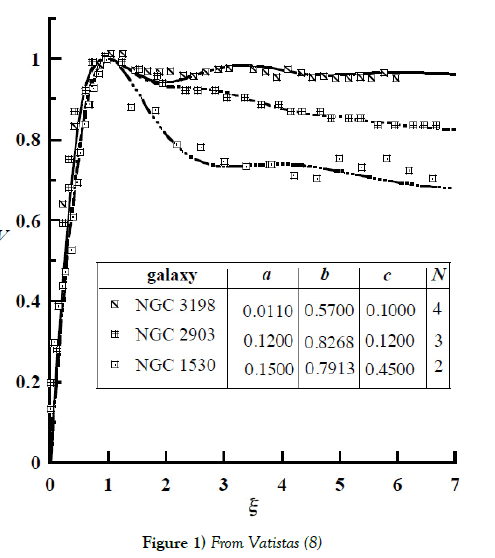
In this section, we discuss a simple model of galaxies based on a postulate of turbulence vortices which govern the galaxy dynamics. Abstract of Vatistas’ paper told clearly [8].

Expanding our previous work on turbulent whirls [1] we have uncovered a similarity within the similarity shared by intense vortices. Using the new information we compress the tangential velocity profiles of a diverse set of vertices into one and thus identify those that belong to the same genus. Examining the Laser Doppler Anemometer (LDA) results of mechanically produced vortices and radar data of several tropical cyclones, we find that the uplift and flattening effect of tangential velocity is a consequence of turbulence. Reasoning by analogy we conclude that turbulence in the interstellar medium could indeed introduce a flattening effect in the galactic rotation curves.

The result of his model equation can yield prediction which is close to observation (without invoking dark matter hypothesis), as shown in the following diagram (Figure 1):

Figure 1) From Vatistas [8]

Therefore, it appears possible to model galaxies without invoking numerous ad hoc assumptions, once we accept the existence of turbulent interstellar medium. The model is also governed by Navier-Stokes equations [8].

Deriving Ermakov-Type Equation for Newtonian Universe with Vortex

It has been known for long time that most of the existing cosmology models have singularity problem. Cosmological singularity has been a consequence of excessive symmetry of flow, such as “Hubble’s law”. A more realistic one is suggested, based on Newtonian cosmology model but here we include the vortical-rotational effect of the whole Universe.

In this section, we will derive an Ermakov-type equation following Nurgaliev [2]. Then we will solve it numerically using Mathematica 11.

After he proceeds with some initial assumptions, Nurgaliev obtained a new simple local cosmological equation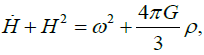: (1)

(1)

Where Here, . stand for Hubble constant, Newtonian gravitational constant, angular speed, and density, respectively.

The angular momentum conservation law ωR²=const=K and the mass conservation law (4π/3) ρR³=const=M makes equation (1) solvable: (2)

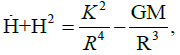(2)

or

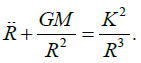(3)

Equation (3) may be written as Ermakov-type nonlinear equation as follows;

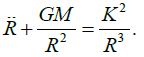(4)

Nurgaliev tried to integrate equation (3), but now we will solve the above equation with Mathematica 11. First, we will rewrite this equation by replacing GM=A, K^2=B, so we get:

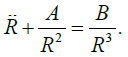(5)

As with what Nurgaliev did in (1,2), we also tried different sets of A and B values, as follows:

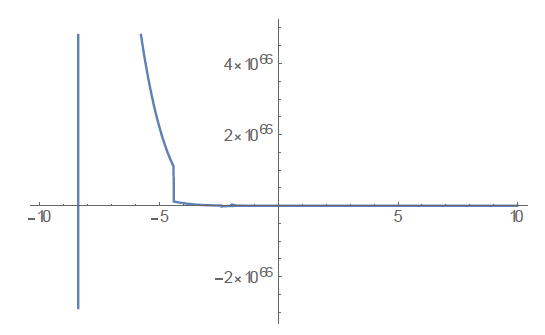
(A) A and B < 0; A=-10; B=-10; ODE=x''[t]+A/x[t]^2-B/x[t]^3==0; sol=ND Solve[{ODE,x[0]==1,x'[0]==1},x[t],{t,-10,10}] Plot[x[t]/.sol,{t,-10,10}].

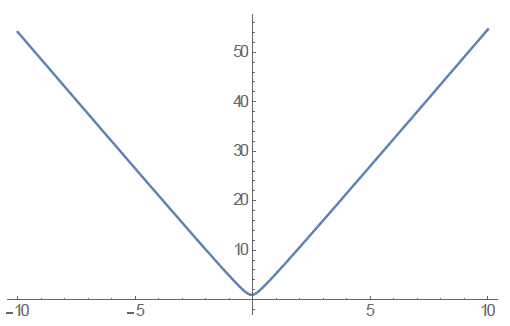
(B) A < 0, B > 0; A=-10; B=10; ODE=x''[t]+A/x[t]^2-B/x[t]^3==0; sol=ND Solve[{ODE,x[0]==1,x'[0]==1},x[t],{t,-10,10}] Plot[x[t]/.sol,{t,-10,10}]

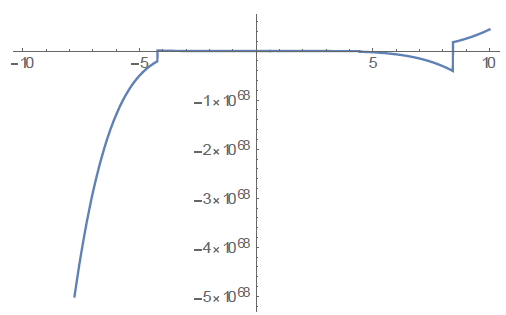
(C) A > 0, B < 0; A=1; B=-10; ODE=x''[t]+A/x[t]^2-B/x[t]^3==0; sol=ND Solve[{ODE,x[0]==1,x'[0]==1},x[t],{t,-10,10}] Plot[x[t]/.sol,{t,-10,10}]

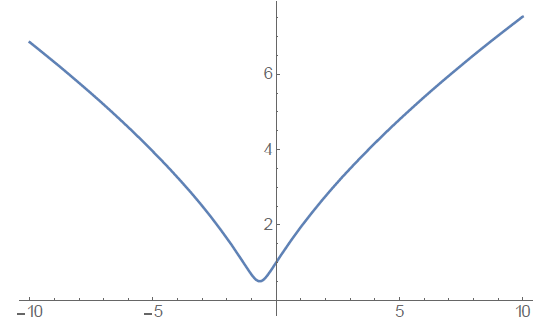
(D) A >0, B > 0; A=1; B=1; ODE=x''[t]+A/x[t]^2-B/x[t]^3==0; sol=NDSolve[{OD E,x[0]==1,x'[0]==1},x[t],{t,-10,10}] Plot[x[t]/.sol,{t,-10,10}]

From the above numerical experiments, we conclude that the evolution of the Universe depends on the constants involved, especially on the rotationalvortex structure of the Universe. This needs to be investigated in more detailed for sure.

Engineering Application: Hurricane Dynamics and Solution of 3d Navier-Stokes

Various methods to describe hurricane dynamics have been proposed in the literature, but most of them are based on 3D Navier-Stokes. Some existing models of tornado dynamics can be found in [9,10].

Now, we will discuss a simplified numerical solution of 3D Navier-Stokes equations based on Sergey Erhskov’s papers [11,12].

In fluid mechanics, there is an essential deficiency of the analytical solutions of Navier–Stokes equations for 3D case of non-stationary flow. The Navier- Stokes system of equations for incompressible flow of Newtonian fluids should be presented in the Cartesian coordinates as below (under the proper initial conditions): [11]

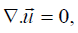(6)

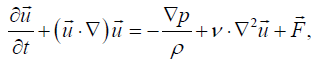(7)

where u is the flow velocity, a vector field; ῥ is the fluid density, p is the pressure, v is the kinematic viscosity, and F represents external force (per unit mass of volume) acting on the fluid [11].

In [11], Ershkov explores the ansatz of derivation of non-stationary solution for the Navier–Stokes equations in the case of incompressible flow, which was suggested earlier. In general case, such a solution should be obtained from the mixed system of 2 coupled Riccati ordinary differential equations (in regard to the time-parameter t). But instead of solving the problem analytically, we will try to find a numerical solution [12-15].

The coupled Riccati ODEs read as follows: [11]

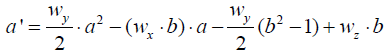(8)

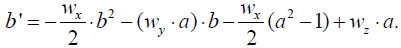(9)

First, equations (8) and (9) can be rewritten in the form as follows:

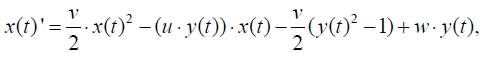(10)

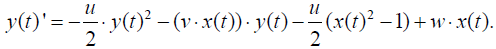(11)

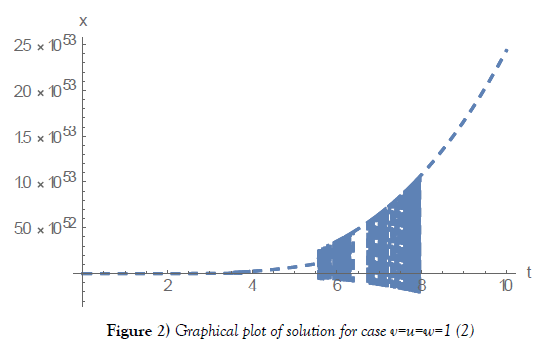
Then we can put the above equations into Mathematica expression: (2)

v=1; u=1; w=1; {xans6[t_],vans6[t_]}={x[t],y[t]}/.Flatten[NDSolve[{x’[t] ==(v/2)*x[t]^2-(u*y[t])*x[t]-(v/2)*(y[t]^2-1)+w*y[t], y’[t]==-(u/2)*y[t]^2- (v*x[t])*y[t]-(u/2)*(x[t]^2-1)+w*x[t], x[0]==1,y[0]==0}, {x[t],y[t]},{t,0,10}]] graphx6=Plot[xans6[t],{t,0,10}, AxesLabel->{“t”,”x”},PlotStyle->Dashing[{0.0 2,0.02}]];Show[graphx6,graphx6]

The result is as shown below Figure 2.

Figure 2) Graphical plot of solution for case v=u=w=1 [2]

It is our hope that the above numerical solution of 3D Navier-Stokes equations can be found useful for engineering purposes, such as controlling large tornadoes which happen quite often in various regions each year.

Conclusion

It has been known for long time that most of the existing cosmology models have singularity problem. Cosmological singularity has been a consequence of excessive symmetry of flow, such as “Hubble’s law”. More realistic one is suggested, based on Newtonian cosmology model but here we include the vortical-rotational effect of the whole Universe. We discuss a plausible model for describing planetary quantization in Solar system and also flattening velocity observed in numerous galaxies. We also review a Riccati-type equation obtained by Nurgaliev, and solve the equation numerically with Mathematica 11.

We also discuss an engineering application of this model, i.e. how to solve 3D Navier-Stokes equations numerically. It is our hope that the above numerical solution of 3D Navier-Stokes equations can be found useful for engineering purposes, such as controlling large hurricanes which happen quite often in various regions each year [16-18].

The solutions obtained here opens up new ways to interpret existing solutions of known 3D Navier-Stokes problem in physics, astrophysics, cosmology and engineering fields, especially those associated with nonlinear hydrodynamics and turbulence modelling [19-20].

It is our hope that the new proposed Cosmology model with vortex can be verified with more extensive observation data.

Acknowledgement

The first author (VC) would like to express sincere gratitude to Sergey Ershkov from Sternberg Astronomical Institute, M.V. Lomonosov’s Moscow State University.

REFERENCES

1. Visser M. Cosmography: Cosmology without Einstein equations. General Relativity and Gravitation. 2004.
2. Ildus S, Nurgaliev E. Peoples Friendship University of Russia (PFUR), Moscow, Russia. Gravitation and Cosmology. 2010;16:313-15.
3. Christianto V, Smarandache F, Umniyati Y. Solving Numerically Ermakov-type Equation for Newtonian Cosmology Model with Vortex. Submitted to Prespacetime J. 2017.
4. Christianto V. A Cantorian Superfluid Vortex and the Quantization of Planetary motion. Apeiron. 2004;11.
5. Christianto V. Comparison of Predictions of Planetary Quantization and Implications of the Sedna Finding. Apeiron. 2004;11.
6. Christianto V. On the origin of macroquantization in astrophysics and celestial motion. Annales de la Fondation Louis de Broglie. 2006;31.
7. Christianto V, Smarandache F. On recent discovery of new planetoids in the solar system and quantization of celestial system. 2005.
8. Vatistas G. The presence of interstellar turbulence could explain the velocity flattening in galaxies.
9. Larcheveque M, Chaskalovic J. A new mathematical model applied to tornado genesis. Int J Engng Sci. 1994;32:187-93.
10. Chaskalovic J, Chauviere A. Appearance of a source/sink line into a swirling vortex. Math. Model and Methods in Appl Sci. 2003;13:121-42.
11. Sergey VE. Non-stationary Riccati-type flows for incompressible 3D Navier–Stokes equations. Computers and Mathematics with Applications. 2016;71:1392-404.
12. Sergey VE. A procedure for the construction of non-stationary Riccati-type flows for incompressible 3D Navier-Stokes Equations. Rend Circ Mat Palermo. 2016;65:73-85.
13. Christianto V, Sergey VE. Solving Numerically a System of Coupled Riccati ODEs for Incompressible Non-Stationary 3D Navier-Stokes Equations.
14. Christianto V, Smarandache F. A Computer Algebra Solution of Ermakov Equation Corresponding to Diffusion Interpretation of Wave Mechanics. Submitted to Prespacetime J. 2017.
15. Shingareva I, Lizarraga CC. Solving Nonlinear Partial Differential Equations with Maple and Mathematica. Dordrecht. 2011:371.
16. Tam PT. A Physicist’s guide to Mathematica. 2nd ed. Amsterdam: Academic Press-an imprint of Elsevier. 2008:749.
17. Landau LD, Lifshitz EM, Fluid mechanics, Course of Theoretical Physics 6, 2nd revised ed., Pergamon Press. 1987.
18. Abu AO. Numerical solutions for the Robin time-fractional partial differential equations of heat and fluid flows based on the reproducing kernel algorithm, International Journal of Numerical Methods for Heat & Fluid Flow. 2017.
19. Abu AO. Fitted reproducing kernel Hilbert space method for the solutions of some certain classes of time-fractional partial differential equations subject to initial and Neumann boundary conditions, Computers & Mathematics with Applications. 2017;73:1243-61.
20. Abu AO, El-Ajou A, Momani S. Constructing and predicting solitary pattern solutions for nonlinear time-fractional dispersive partial differential equations, Journal of Computational Physics. 2015;293:385-99.