Abundant M-Fractional Exact Solutionsfor STOand (3 + 1)-Dimensional KdV-ZK Equations via (m + (G\'/G))-Expansion Method

Received: 18-Feb-2021 Accepted Date: Mar 01, 2021; Published: 09-Mar-2021, DOI: 10.37532/2752-8081.21.5.28

Citation: Ali S. Abundant M-Fractional Exact Solutions for STO and (3 + 1)-Dimensional KdV-ZK Equations via (m + (G′/G))-Expansion Method. J Pur Appl Math. 2021; 5(3):38:42.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

In the field of applied mathematics, fractional calculus is used to contract with derivative as well as the integration of any power. Different definitions of the fractional derivative have been introduced in the literature. For example, these are some important definitions of fractional derivatives, Riemann-Liouville derivative, Caputo derivative and conformable derivative. Recently the generalization of the conformable derivative has been given as M-fractional conformable. Fractional differential equations (FDEs) “equations involving fractional derivatives” are employed invarious areas of science and engineering and others [1-5] have widely been interested. That’s why they have gained many attractions from many researchers. To acquisition, the analytical solutions of the FPDEs is a conspicuous look of scientific research.

Keywords

Fractional Derivative, Riemann-Liouville derivative, Conformable derivative and numerous scholars

Introduction

Consequently, numerous scholars have developed some persuasive methods to acquired approximate and exact solutions for these types of FPDEs. In this investigation, the truncated M-fractional conformable (STO) and (3 + 1)-dimensional KdV-ZK equations are considered. The novel method: (m + G’ )-expansion method are utilized to extract the exact solitons of the aforesaid model equations. Different definitions of fractional derivatives have appeared in the literature. For example, Reimann-Liouville [1], Caputo derivative and conformable derivative. Despite these two most recent definitions are reported as M-fractional conformable and beta derivatives. Many powerful techniques have been reported in the literature for finding exact solutions, see for example [5-9]. Fortunately, it is possible to establish a traveling wave transformation for a fractional order PDE which can convert it to a nonlinear ordinary differential equation (NODE) that can be easily solved by using a variety of different methods. There are many distinct techniques have been applied to gain the exact solitons of (STO) and (3 + 1)-dimensional KdV-ZK equations like : F-expansion method and Improved - expansion methods are used to obtain the bright, dark 1-soliton and other soliton solutions [10], new extended direct algebraic technique is implemented to gain the number of new type of solitons of the conformable fractional (STO) equation [11], dark and bright optical solitons gained by variable coefficient method [12], dispersive exact wave solutions are observed by modified simplest equation method [13], different optical solitons of the (STO) equation are achieved by applying the extended trial method [14], Extended sinh-Gordon equation expansion scheme has utilized to obtain different types of optical solitons of STO equation [15], extended auxiliary equation scheme is applied to gain the dispersive optical wave solitons of time-fractional (SH) equation along power law non-linearity as well as Kerr Law non-linearity [16], undetermined coefficient method is implemented to gain the distinct kinds of dispersive exact solitons in the presence of several perturbation terms are achieved [17], with the use of tanh- coth integration algorithm dispersive solitons in optical nanofibers are obtained with constraint conditions [18], by using the Sine-Cosine function method, different exact solutions are obtained [19], Sech, Tanh and Csch function techniques are utilized to gain the optical solitons of (STO) equation along Kerr law non-linearity [20]. There are many applications of the Sine-Gordon expansion method and (m + G′/G) -expansion method. For instance, with the use of Sine Gordon-expansion scheme, distinct kinds of solitons of the non-linear time-fractional Biological Population equation and the Cahn- Hilliard model have been obtained in [21], hyperbolic and trigonometric functions solitons to the non-linear reaction diffusion equation have achieved [22] etc.

Similarly, (m + G′/G)-expansion method has been utilized to solve the Pochhammer-Chree equations for bell-shaped, kink-shaped and periodic type solitons of with the help of this method [23], discrete and periodic type solitons of the Ablowitz-Ladik lattice system are found [24] etc.

To find the exact solutions of integrable partial differential equations is the most interesting topic. Therefore, we will solve two integrable model equations namely space-time fractional Sharma Tasso-Olever (STO) and space- time fractional (3+1)-dimensional KdV-ZK equations for a variety of solitons with a novel derivative operator by employing (m + G′/G)- expansion method: Abundant M-Fractional Exact Solutions for STO and (3+1)-Dimensional KdV-ZK Equations via (m + G′/G)-Expansion Method

2 Description of (m + G′/G)-Expansion method

In this section, the basic concept of the (m + G/G) method are illustrated as bellow:

Step:1

Assume that the general form of NLPDE is expressed as

                      (1)

Suppose the Wave transformation takes the following form:

                      (2)

Inserting eq.(2) into eq.(1),we obtain

                      (3)

Step:2

Suppose that the trial solution of eq.(3) is given by

                      (4)

where cn, n = 0, 1, , , , , , , , n and m are nonzero constants.

According to the principles of balance,we find the value of n.In this article we define F as

                      (5)

where G(ξ) satisfies,the second order nonlinear ODE:

                      (6)

The Cole-Hopf transformation F = ln(G(ξ))ξ = G’(ξ) reduces equation into the Reccati equation

                      (7)

Substitute equation (4) including Eq. (7) and Eq. (5) into Eq. (3), then we will obtain polynomials in [d + G’(ξ) ]j and

[d + G’(ξ) ]−j ,(j = 0, 1, 2, 3, , N ).

Collect each coefficient of the resulting polynomials and let it be zero. We can obtain the following twenty seven solutions [25-46]

Applications

STO equation by (m+G’/G)

Consider the space-time fractional order STO equation

                      (8)

Using the transformation

                      (9)

((8)) can be changed into an ODE equation

                      (10)

Using the balance principle we get n = 1, so eq. (4) reduces to

                      (11)

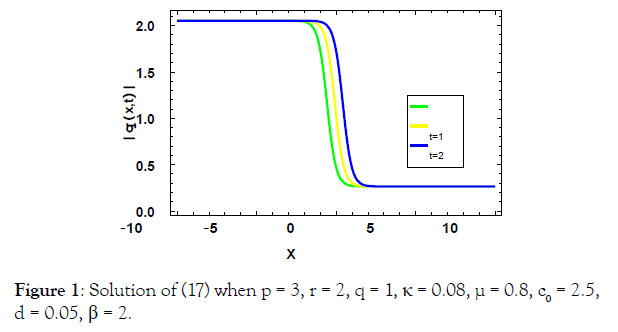
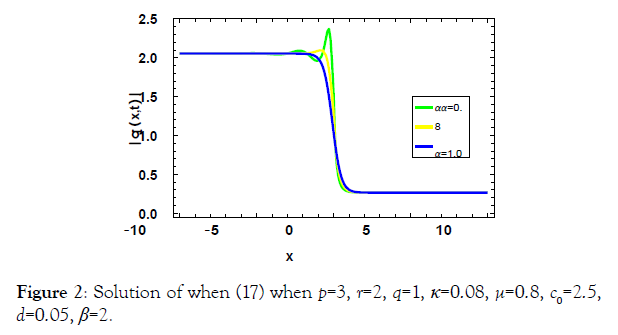
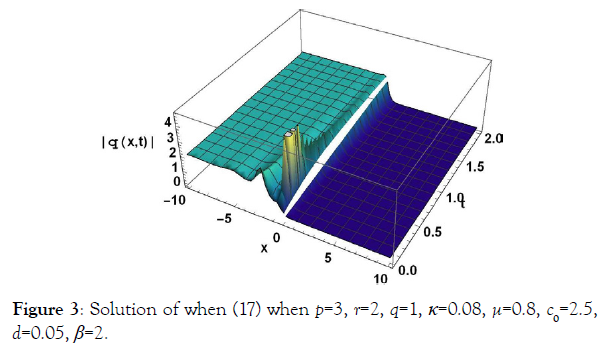
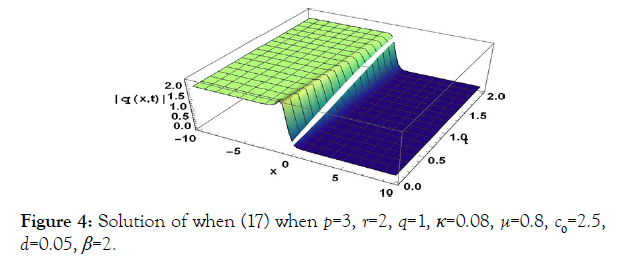
After solving the algebraic equations of (10) we obtained variety of solutions as follows:

Case 01

                      (12)

Case 02

                      (13)

Case 03

                      (14)

Case 04

                      (15)

Case 05

                      (16)

Solution 1

(Corresponding case 01)

Type 01: When p2 − 4q(r − 1) > 0 and p(r − 1) /= 0 (orq(r − 1) =/ 0) the solution of Eqs(10)

Where A and B are two non-zero real constants and Satisfies B2 − A2 > 0

Figure 1: Solution of (17) when p = 3, r = 2, q = 1, κ = 0.08, μ = 0.8, c₀ = 2.5, d = 0.05, β = 2.

Figure 2: Solution of when (17) when p=3, r=2, q=1, κ=0.08, μ=0.8, c₀=2.5, d=0.05, β=2.

Figure 3: Solution of when (17) when p=3, r=2, q=1, κ=0.08, μ=0.8, c₀=2.5, d=0.05, β=2.

Figure 4: Solution of when (17) when p=3, r=2, q=1, κ=0.08, μ=0.8, c₀=2.5, d=0.05, β=2.

Figure 5: Solution of when (17) when p=3, r=2, q=1, κ=0.08, μ=0.8, c₀=2.5, d=0.05, β=2.

Figure 6: Solution of (29) when p=1, r=2, q=1, κ=0.06, μ=0.5, c₀=4.5, d=0.08, β=2.

Figure 7: Solution of (29) when p=1, r=2, q=1, κ=0.06, μ=0.5, c₀=4.5, d=0.08, β=2.

Figure 8: Solution of (29) when p=1, r=2, q=1, κ=0.06, μ=0.5, c₀ =4.5, d=0.08, β=2.

Figure 9: Solution of (29) when p = 1, r= 2,q = 1, κ= 0.06, μ = 0.5, c₀ = 4.5, d = 0.08, β= 2.

Figure 10: Solution of (29) when p=1, r=2, q=1, κ=0.06, μ=0.5, c₀=4.5, d=0.08, β=2.

Solution 04 (Corresponding case 04)

Type:04 When (r-1)/=0andq=p=0the solutions of Eqs(10)

1

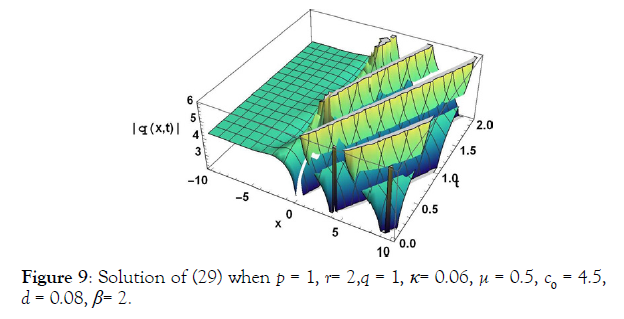
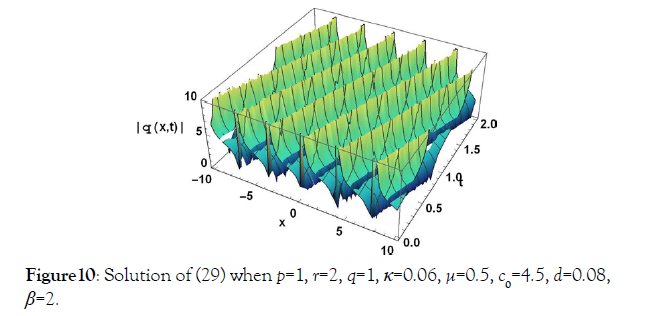
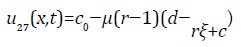              (70)

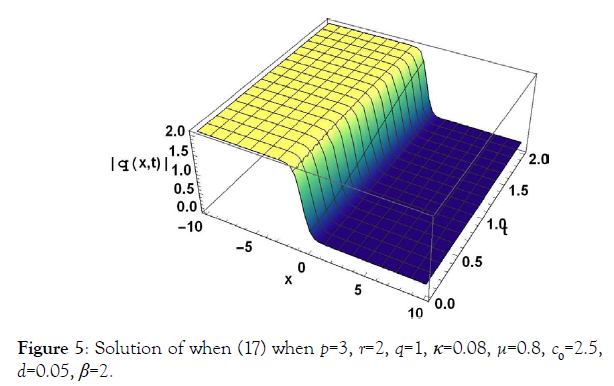
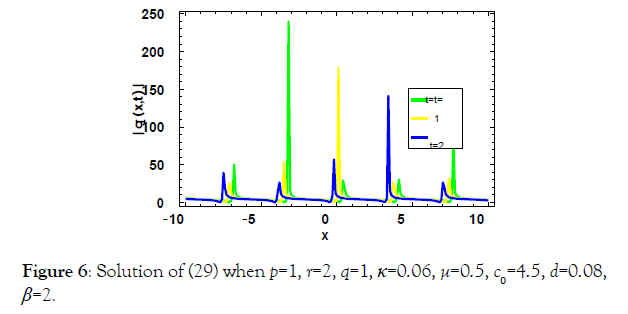
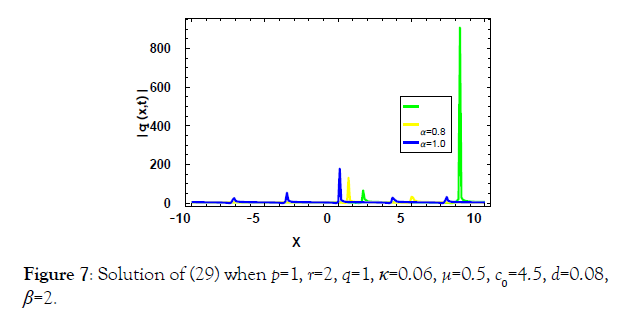
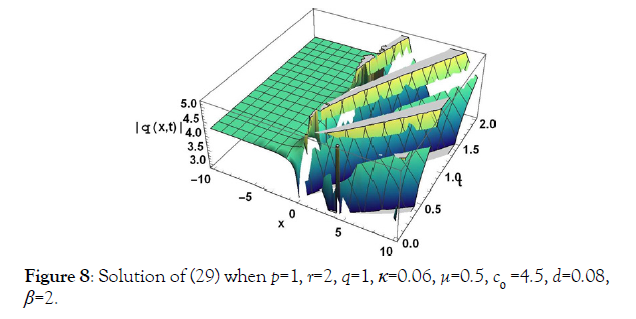
Applications

4 Kdv-ZK equation by (m + G′/G)

Space-time fractional Kdv-ZK equation

consider the space-time fractional Kdv-ZK equation [19]

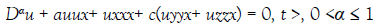              (71)

and the transformation

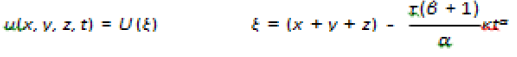              (72)

Where κis nonzero constant,which on substituting in (71) give us the following ODE

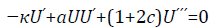              (73)

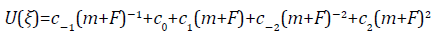              (74)

Case 01

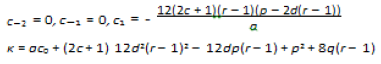
REFERENCES

1. Podlubny I. Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Elsevier. 1998; 27.
2. Inan IE, Ugurlu Y, Bulut H. Auto-Bäcklund transformation for some nonlinear partial differential equation. Optik. 2016;127(22):10780-5.
3. Wazwaz AM. Multiple-soliton solutions for the KP equation by Hirota’s bilinear method and by the tanh–coth method. Applied Mathematics and Computation. 2007;190(1):633-40.
4. Zayed EM, Alurrfi KA. A new Jacobi elliptic function expansion method for solving a nonlinear PDE describing the nonlinear low-pass electrical lines. Chaos, Solitons & Fractals. 2015;78:148-55.
5. Naher H, Abdullah FA, Mohyud-Din ST. Extended generalized Riccati equation mapping method for the fifth-order Sawada-Kotera equation. AIP Advances. 2013;3(5):052104.
6. Sakar MG, Ergören H. Alternative variational iteration method for solving the time-fractional Fornberg–Whitham equation. Applied Mathematical Modelling. 2015;39(14):3972-9.
7. Abdou MA, Soliman AA. New applications of variational iteration method. Physica D: Nonlinear Phenomena. 2005;211(1-2):1-8.
8. Soliman AA. The modified extended direct algebraic method for solving nonlinear partial differential equations. Int J Sci. 2008;6(2):136-44
9. Elwakil SA, El-Labany SK, Zahran MA, Sabry R. Modified extended tanh-function method for solving nonlinear partial differential equations. Physics Letters A. 2002;299(2-3):179-88.
10. Zhang S, Xia T. An improved generalized F-expansion method and its application to the (2+ 1)-dimensional KdV equations. Communications in Nonlinear Science and Numerical Simulation. 2008;13(7):1294-301.
11. Navickas Z, Ragulskis M, Listopadskis N, Telksnys T. Comments on “Soliton solutions to fractional-order nonlinear differential equations based on the exp-function method”. Optik. 2017; 223-231.
12. Navickas Z, Telksnys T, Ragulskis M. Comments on “The exp-function method and generalized solitary solutions”. Computers & Mathematics with Applications. 2015;69(8):798-803.
13. Manafian J, Lakestani M. Application of tan (ϕ/2)-expansion method for solving the Biswas–Milovic equation for Kerr law nonlinearity. Optik. 2016;127(4):2040-54.
14. Akbulut A, Kaplan M, Tascan F. The investigation of exact solutions of nonlinear partial differential equations by using exp (−Φ (ξ)) method. Optik. 2017;132:382-7.
15. Li ZB, He JH. Fractional complex transform for fractional differential equations. Mathematical and Computational Applications. 2010;15(5):970-3.
16. Wen-An L, Hao C, Guo-Cai Z. The (ω/g)-expansion method and its application to Vakhnenko equation. Chinese Physics B. 2009;18(2):400..
17. Zhang Y. Solving STO and KD equations with modified Riemann– Liouville derivative using improved $(G’/G) $-expansion function method. IAENG Int J Appl Math. 2015;45(1):16-22.
18. Kilbas AA, Srivastava HM, Trujillo JJ. Theory and applications of fractional differential equations. elsevier; 2006.
19. Kadem A, Kılıçman A. Note on transport equation and fractional Sumudu transform. Computers & Mathematics with Applications. 2011;62(8):2995-3003.
20. Gao GH, Sun ZZ, Zhang YN. A finite difference scheme for fractional subdiffusion equations on an unbounded domain using artificial boundary conditions. Journal of Computational Physics. 2012;231(7):2865-79.
21. Afzal I. Stationary Solutions and Optical Solitons for Nonlinear Schrodinger Equations (Doctoral dissertation, Department of Mathematics, COMSATS University Islamabad, Lahore campus).
22. Ekici M, Mirzazadeh M, Sonmezoglu A, Ullah MZ, Asma M, Zhou Q, Moshokoa SP, Biswas A, Belic M. Dispersive optical solitons with Schrödinger–Hirota equation by extended trial equation method. Optik. 2017;136:451-61.
23. Naher H, Abdullah FA. Some New Traveling Wave Solutions of the Nonlinear Reaction Diffusion Equation by Using the Improved (G′/G)- Expansion Method. Mathematical Problems in Engineering. 2012.
24. Bulut H, Sulaiman TA, Baskonus HM, Aktürk T. On the bright and singular optical solitons to the ($ $2+ 1$$2+ 1)-dimensional NLS and the Hirota equations. Optical and Quantum Electronics. 2018;50(3):1-2.
25. Zhang Y. Solving STO and KD equations with modified Riemann– Liouville derivative using improved $(G’/G) $-expansion function method. IAENG Int J Appl Math. 2015;45(1):16-22.
26. Kaur L, WazwazAM. Bright–dark optical solitons for Schrödinger-Hirota equation with variable coefficients. Optik. 2019; 179:479-84.
27. Yaşar E, Yıldırım Y, Zhou Q, Moshokoa SP, Ullah MZ, Triki H, Biswas A, Belic M. Perturbed dark and singular optical solitons in polarization preserving fibers by modified simple equation method. Superlattices and Microstructures. 2017;111:487-98.
28. Zhou Q, Ekici M, Sonmezoglu A, Mirzazadeh M. Optical solitons with Biswas–Milovic equation by extended G′/G-expansion method. Optik. 2016;127(16):6277-90.
29. Zhou Q, Ekici M, Sonmezoglu A, Mirzazadeh M, Eslami M. Optical solitons with Biswas–Milovic equation by extended trial equation method. Nonlinear Dynamics. 2016;84(4):1883-900.
30. Hassaballa AA, Elzaki TM. Applications of the improved G/G expansion method for solve Burgers-Fisher equation. Journal of Computational and Theoretical Nanoscience. 2017;14(10):4664-8.
31. Khalil R, Al Horani M, Yousef A, Sababheh M. A new definition of fractional derivative. Journal of Computational and Applied Mathematics. 2014;264:65-70.
32. Sulaiman TA, Bulut H, Baskonus HM. Optical solitons to the fractional perturbed NLSE in nano-fibers. Discrete & Continuous Dynamical Systems-S. 2020;13(3):925.
33. Ray SS. Dispersive optical solitons of time-fractional Schrödinger–Hirota equation in nonlinear optical fibers.Physica A: Statistical Mechanics and Its Applications. 2020;537:122619.
34. Sardar A, Ali K, Rizvi ST, Younis M, Zhou Q, Zerrad E, Biswas A, Bhrawy A. Dispersive optical solitons in nanofibers with Schrödinger- Hirota equation. Journal of Nanoelectronics and Optoelectronics. 2016;11(3):382-7.
35. Sardar A, Ali K, Rizvi ST, Younis M, Zhou Q, Zerrad E, Biswas A, Bhrawy A. Dispersive optical solitons in nanofibers with Schrödinger- Hirota equation. Journal of Nanoelectronics and Optoelectronics. 2016;11(3):382-7.
36. Mohamad-Jawad AJ. The Sine-Cosine Function Method for Exact Solutions of Nonlinear Partial Differential Equations. Journal of Al Rafidain University College. 2013(32):124-43.
37. Kilic B. Improved šG 0/GŽ-Expansion Method for the Time-Fractional Biological Population Model and Cahn–Hilliard Equation. Journal of Computational and Nonlinear Dynamics. 2015 Sep;10:051016-1.
38. Zuo JM. Application of the extended G′ G-expansion method to solve the Pochhammer–Chree equations. Applied mathematics and computation. 2010 Sep 1;217(1):376-83.
39. Zuo JM. Application of the extended G′ G-expansion method to solve the Pochhammer–Chree equations. Applied mathematics and computation. 2010 Sep 1;217(1):376-83.
40. Jumarie G. Table of some basic fractional calculus formulae derived from a modified Riemann–Liouville derivative for non-differentiable functions. Applied Mathematics Letters. 2009 Mar 1;22(3):378-85.
41. He JH, Li ZB. Converting fractional differential equations into partial differential equations. Thermal Science. 2012 Jun 1;16(2):331-4.
42. Bulut H, Sulaiman TA, Baskonus HM, Rezazadeh H, Eslami M, Mirzazadeh M. Optical solitons and other solutions to the conformable space–time fractional Fokas–Lenells equation. Optik. 2018 Nov 1;172:20-7.
43. Ismael HF, Bulut H, Baskonus HM. Optical soliton solutions to the Fokas–Lenells equation via sine-Gordon expansion method and $$(m+ ({G’}/{G})) $$(m+ (G′/G))-expansion method. Pramana. 2020 Dec;94(1):1-9.
44. Cattani C, Sulaiman TA, Baskonus HM, Bulut H. On the soliton solutions to the Nizhnik-Novikov-Veselov and the Drinfel’d-Sokolov systems. Optical and Quantum Electronics. 2018 Mar;50(3):1-1.
45. Gao W, Ghanbari B, Günerhan H, Baskonus HM. Some mixed trigonometric complex soliton solutions to the perturbed nonlinear Schrödinger equation. Modern Physics Letters B. 2020 Jan 30;34(03):2050034.
46. Zhu SD. The generalizing Riccati equation mapping method in non-linear evolution equation: application to (2+ 1)-dimensional Boiti– Leon–Pempinelle equation. Chaos, Solitons & Fractals. 2008 Sep 1;37(5):1335-42.