Enhanced comprehension of the quantum mechanical hidden variables

Received: 24-Dec-2022, Manuscript No. PULJMAP-22-5849; Editor assigned: 28-Dec-2022, Pre QC No. PULJMAP-22-5849(PQ); Accepted Date: Jan 24, 2023; Reviewed: 06-Jan-2023 QC No. PULJMAP-22-5849(Q); Revised: 16-Dec-2022, Manuscript No. PULJMAP-22-5849(R); Published: 29-Jan-2023, DOI: 10.37532/ puljmap.2023 .6(1); 01-03

Citation: Koutandos S. Enhanced comprehension of the quantum mechanical hidden variables. J Mod Appl Phys. 2023; 6(1):1-3.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

We investigate the repercussions of the hypothesis that the volume is altering because of a mass-induced curvature in spacetime. The various thermodynamic quantities take on a local character as a result of the representation of the electron's dipolar nature. In this article, extensive research is continued, and fresh findings are made, further hidden-variable theories in physics propose to explain quantum mechanical events by introducing imaginary (and sometimes unobservable) entities. The mathematical formulation of quantum mechanics makes the assumption that some measurements are fundamentally indeterminate; additionally, the Heisenberg uncertainty principle allows for the quantification of the constraints on indeterminacy. The majority of hidden-variable theories aim to avoid quantum indeterminacy, albeit this may need require the existence of nonslocal interactions.

Keywords

Quantum thermodynamics; Hidden variables of quantum mechanics; Quantum mechanics; Free energy

Introduction

The main logical controversy in quantum mechanics is that thereare point particles. We have solved this issue by proposing that mass should alter space time and induce a space-time curvature. In that case we should have a fluid space time as well as the creation of volume.

The equations for fluid space-time are simple:

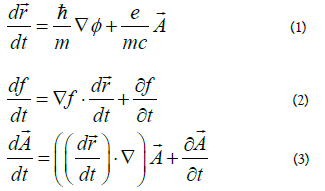
Through the use of equations (1), (2) and (3) we were able to prove London equations in superconductivity. With the further assumptions described in the main part ahead Ginzburg-Landau expansion of free energy for superconductors was given a more physical insght.

In what is to foll0ow the reader is advised to look up at the references included in the last section for more detailed proofs [1-9].

We made the assumption that the volume of the electron or the point particle varies locally as a result of our research.

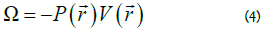
In our work [1] we have proved that the logarithm of probability per volume is the entropy as expected from simple statistical physics arguments:

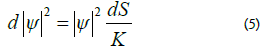
Considering that pressure is correlated with a local variation in temperature, the formula for pressure is as follows:

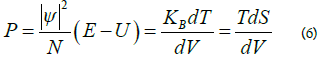
It was also proved that psi squared represents the pressure density as well, a pressure which originates from the equivalence principle applicated:

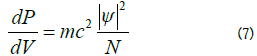
Equation (7) results in:

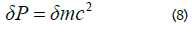
Equations (4), (5), (6), (7) result [1] in the stability of free energy:

We define the true probability (opposite to the probability per volume) as:

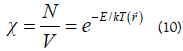
So in that sense the local probability is inversely proportional to the volume as expected.

The dielectric susceptibility is represented by the left side of equation (10). As predicted by Einstein, mass affects the speed of light, according to the author's findings. The equations that we present are as follows:

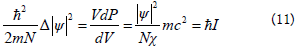
In equation (11) P stands for the pressure. Another formula also is the result of our research:

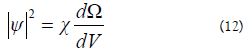
In formula (12) Omega stands for the solid angles of the observer. Combining formulas (10) and (12) we arrive to the conclusion that chi describes yet another form of probability:

Using equations (6) and (11) we find:

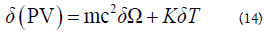
The dipolar nature of the particles should be blamed for these phenomena. We use the force density's divergence to determine the bulk modulus, and the outcome seems reasonable. Therefore:

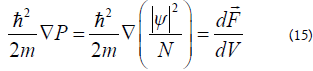
The dipolar character of the particles should be blamed for these events. We use the force density's divergence to get the bulk modulus, and the outcome appears fair. Therefore:

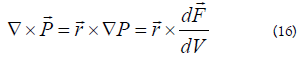
The vorticity, a quantity which in our research has helped explain London s equations is found to be:

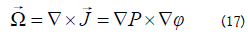
Due to the fact that velocity in quantum mechanics is different for the derivative of the radius compared to time, another formula has provided insight into this series of investigations. More specifically:

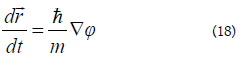
With the help of equations (15) and (18) vorticity (in the absence of magnetic field for simplicity ) is written as:

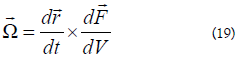
The polarization charge density is associated with the virial theorem actually:

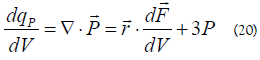
Discussion

An underpinning broad mathematical framework for physical theory is produced by a small collection of axioms and definitions that are justified by operational considerations. This structure is known as the orthomodular or "orthological" structure of physical problems and probabilities. This structure must be further realised or described in terms of a computationally practical structure in order for it to be helpful. We are left with the two models that are currently in use: the classical or Boolean orthologic (Boolean algebra) and the quantum or Hilbert orthologic, until someone figures out a method to do this more directly, utilising simply the qualities intrinsic to the physical ortholattice (subspace of a Hilbert space). Both of these models cannot be ruled out due to their inability to handle complex physical situations, as we noted in Section IV. Consequently, efforts to prove generally, Therefore, efforts to generally demonstrate the impossibility of Boolean hidden variable theories would appear to be fruitless, much like efforts to demonstrate the impossibility of Hilbert orthologics' ability to encompass all physical issues and probability measures. Of course, experimentation can be used in either situation to disprove the mathematical model's associations between certain physical constituents and specific objects. Therefore, it is important to make a clear distinction between general mathematical languages (such as Hilbert ortholattices and Boolean algebras) and specific theories expressed in these languages.

Conclusions

We have attempted to solve the main dilemma of physics concerning the existence of point particles. The dielectric susceptibility alters the speed of light due to the existence of mass in spacetime. It is represented by the Greek letter chi which comes before psi and it is found to represent the true probability. As the volume is changing due to temperature dilation from the relativistic equivalence principle the solid angles with whic-h the observer observes are changing. The dipolar nature of the charge splits space and creates these phenomena.

We would like to add that through the course of our research we have found a lot of symbolism in quantum mechanical quantities which gives further proof for the existence of hidden variables. We hope that we have contributed to this field and hope that there will come further proof from other researchers.

References

1. Koutandos S .Assigning physical quantities to the hidden variables of quantum mechanics. Glo J for Res Anal. August 2022.
2. Koutandos S. An Advanced Study Explaining Ginzburg Landau Equations from First Principles, Newest Updates Phys. Sci. Res 10;2021:74-9.

   [Google scholar][Crossref]

3. Koutandos S.Is Schrodinger equation a relativistic effect? , Phys Sci. Biophys. J. 2021,.5(1)
4. Koutandos S. Regarding the formalism of quantum mechanics, Phys Sci. Biophys. J. 2021;.5(1)
5. Koutandos S. .Exploring the possibility of surface change during Emission of Radiation for the electron, Phys Sci. Biophys. 2021, J.5(1).
6. Koutandos S. Erratum on the author's work so far, Phys Sci. Biophys. 2021, J.5(1).
7. Koutandos S..About a possible derivation of the London equations,Physics Essays;3 (2); 208-10
8. Koutandos S. Regarding the Total Time Derivative of the Radius. IOSR J Appl Phys.2018;10(6): 26-27
9. Koutandos S. An Advanced Study Explaining Ginzburg Landau Equations from First Principles. Newest Updates in Physical Science Research. 10;2021;74-9.

   [Google Scholar][Crossref]