Grand unified theory using permutation group s4 applied to Einstein’s equation
Received: 09-Dec-2024, Manuscript No. PULJPAM-23-6636; Editor assigned: 12-Dec-2024, Pre QC No. PULJPAM-23-6636 (PQ); Reviewed: 01-Jan-2024 QC No. PULJPAM-23-6636; Revised: 10-Jan-2025, Manuscript No. PULJPAM-23-6636 (R); Published: 21-Jan-2025
Citation: Felde KZ. Grand unified theory using permutation group s4 applied to Einstein's equation. J Pure Appl Math. 2025;9(1):1-4.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
We give an informal, brief introduction to string theory. We introduce a new concept, where the whole system of all four forces, is described by one single group, the permutation group S4 and where gravity has eleven dimensions, d=4, i.e., space time and seven internal dimensions. Thus D=11 since the permutation group contains all forces that are known, we can call this a grand unified theory. The additional seven dimensions, six spatial and one dilaton are internal dimensions, that are compactified and are contributing to finally receive D=11 dimensions. Since there’re two super symmetric partners, the quarks and the particle strings from the weak interaction, we receive N=2.
Keywords
String theory; de Moivre's theorem; A solvable quintic equation; A solvable sextic equation; A solvable bisextic equation
Introduction
Physicists introduced theories where the smallest entities aren’t points but strings or objects like, F.e., tiny balls. Thus they got additional dimensions. They got mass and spin and charge and other properties that are a result of quantized vibrations.
In 1969-70, Nambu, Nielsen, and Susskind have been presented a physical interpretation of the π, π scattering, by introducing vibrating one dimensional string [1-4].
1971 Ramond, Neveu and Schwarz found a way to incorporate fermions into the puzzle This is called the RNS formalism. This approach shows conformal invariance [5,6].
In 1974, Schwarz, Scherk and Yoneva found that a bosonic theory has been led to discover the graviton in string theory [7,8].
There have been proposed five consistent versions of superstring theory. Those seem to be all different cases of the so called M-theory that contains eleven dimensions. String theory has two problems. It is not easy to find out the correct theory, because it has so many types of freedom. Das has made a pertubation expansion, showing that the whole Dirac Sea is contributing to the degrees of freedom [9]. And the full theory seems to be a real puzzle, since it doesn’t cover every necessary feature that is needed.
String theory requires super symmetry. Super symmetry is a property of a compound of fermionic and bosonic strings, which let total spin invariant until the super symmetry is lost while fermions and bosons discouple.
A string moves, by being mathematically represented the world sheet, since its movement covers a two dimensional surface. The goal of string theorists is to find the correct action and therefore also the correct symmetry group, since it is necessary that the objects are decaying into the correct objects i.e., a simple model of the bosonic string in Minkowski spacetime shows Poincare, reparametrization and Weyl transformation invariance. Poincare invariant is a global invariance since it is an infinitesimal Lorentz invariance. Reparametrization is invariance of point in space time and Weyl transformation invariance is scale invariance. It doesn’t matter from which distance you look at the system; it has the same physical properties. This is called conformal invariance and results in the fact that super symmetric strings are Ricci flat, i.e., Rμv=0. In other words the world of strings is smooth.
It is necessary that super symmetry is the origin of the theory F.e., the graviton is put together with two Dirac fermions, together are forming a super symmetric entity with spin zero. String theory introduces extra dimensions that are a result of looking close to that particle. F.e., one can imagine a point being a ball if one looks at it at a distance close to l ~10-35m.
The correct symmetry group is necessary, since it got the correct physical properties. Since string theory rely on the length l, it contains no such singularities, like point particles.
The internal space of a string is called a p-brane. It can be regarded as a space with spatial dimensions.
A IIB theory that is SL (2, Z) invariant, better conformal invariant, which says that transformations are mapping circles into circles and lines into lines. The Moebius transformation saves angles and is examined by Schwarz [10,11].

T-duality has been discovered in the eighties [12]. It is revealing the identity of two theories, that are either proportional to the radius 2π·R, or to 1⁄R. We are able to state, that T-duality appears to be a special case of conformal duality.
Witten E, revealed, that T-duality, which is saying two theories that are dual are basically transforming the same way [13]. Before duality, there were existing five basic string theories, e.g., bosonic, I, IIA, IIB, HO and HE. Now suppose we take one of the ten dimensions and form a circle. A string is winding around this circle R n times are leading to the fact that there will be many different states for large R and for small R. It follows IIA theories are bascially the same as IIB theories.
Another approach is F-theory by Vafa that is too based on the group SL (2, Z). This group is describing a torus [14]. A torus is a map from euclidean coordianates a £ Z ⊕ b £ Z that are forming a lattice to the complex plane S £ C. The torus is then given by: z ~ z+a ~ z+b, with b⁄a are defining the shape of the torus. F-theories are based on IIB strings. Those are strings that contain only one chirality.
F-theory is a 12-dimensional theory. Commonly Calabi-Yau manifold theory is used to describe spacetime. F-theory has the metric signature (10, 2),which means that it includes a second time dimension. The two-torus has been compactified to two dimensions.
A torus is invariant under a Moebius transformation, which preserves angles and transforms circles into circles and lines into lines. Equation 1 can be decomposed in three single transformations:
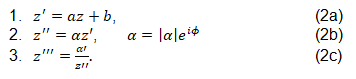
By z'''=(x+iy), z''=(x-iy), we receive α'=x2+y2. This is the string coupling constant. The only free parameter in string theory. It can take any value between 10-35 m and 1019 m.
The dimension full parameter, α', is of dimension:

The intrinisic length and mass scales of the theory are thus ls=2π•√(α') is the string length and M=1/√(α'), is the string mass scale.
Interestingly, the conformal transformation reveals conformal duality. Since α'=(m2), we are discussing the result of a stereographic projection onto a two dimensional disc with radius r. The formula for the plane is F=π.r2. If we are setting: z'''=r.sinλ, z''=r,α' is fixed. Thus α' is the geodesic curvature, which is growing until λ=π⁄ 2. Thus a conformal theory is always dual:

With (2c) a new dimensional parameter appears: the dilaton, i.e., φ. We are able to quantize α', by:
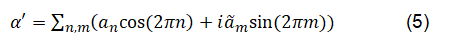
Dualities are revealing everywhere in string theory and physics. F.e., the electric and magnetic fields are exchangeable.
We are discussing a circle. If you increase z, call this increasement δz1 at one point, at a point perpendicular to z, the circle has been decreased by - δz2. The object is now an ellipsis. The increasement is resulting to 1⁄Rgeo and the decreasement to Rgauss. Since the increasement and the decreasement are automatically following each other, one is able to say that theory is dual, equation 4 is holding.
A closed string, that is T-dual, where one dimension of 26 spatial dimensions is a circle, is called compactified on a circle of radius R. T-duality is a transformation of R→ R'=α/R. It leaves the mass formula invariant. This can be compared with Newton’s formula which can be transformed into the Coulomb law by setting.
It follows that:
If we look from a distance on the system, the additional dimensions aren’t visible. To verify this one uses compactification. F.e., a bosonic string, which has 26 dimensions, is divided into 25 dimensions, that are winding around a center, which is described by a winding number, and recognized as the 26th dimension, 2π•R•ω, where ω is the winding number.
The problem with super symmetric string theory is, that there are too many different solutions. Are there only N=1 super symmetry partners or are there more? It is needed to identify different fermionic partners that are connected. Interestingly the electron doesn’t have an internal structure. Does the proton has a connection to gravity or is this restricted to the quarks? The proton and the neutron play a role in the weak interaction. Here the neutron plays a special role. The weak interaction is governed by the neutron which is the only particle interacting with all other three particles.
The strong interaction is mediated by gluons. The gluons are connected to their fermionic partners.
In Raymond-Neveu-Schwarz theory, RNS, D dimensional bosonic string theory contain D fermionic fields [15,16]. The fermionic fields are twocomponent spinors which describe entities that are existing on the worldsheet and transform as vectors under a Lorentz transformation on D dimensional spacetime. They are assuming that the numbers of bosonic and fermionic degrees of freedom are the same. RNS show that their actions are really describes a superstring theory. This superstring theory is called a RNS superstring theory since the theory has supersymmetry on the worldsheet, as opposed to the Green-Schwarz (GS) superstring theory [16,17]. The GS theory cancels all gauge anomalies, mixed anomalies, and gravitational anomalies. Anomalies are relicts of the limit of a symmetry breaking parameter went to zero.
A mystic role is playing by M-theory. For mathematical reasons, M-theory takes place in eleven spactime dimensions. Strings seem to be noticed in our universe as vibrating objects. The nature of vibrations decides if the string shows mass or energy. The problem is which the correct description of nature is. Witten has introduced as the first M-theory [13,18]. There’s some evidence, that an eleventh dimension is real says Witten [13]. We are coming to the same conclusion, since one part of the permutation group S4 is representing a scalar. This scalar is identfied as a Higgs at higher energy being the product of the parameter α' multiplied by eiÃÃÃÂ??ÂÃÂ?ÂÂ?, where ÃÃÃÂ??ÂÃÂ?ÂÂ? is the dilaton.
Grand unified theory of permutation symmetry group S4 realized by Einstein’s equation
We believe that there’s a problem with the description of reality of the standard model. It is missed a link between a, to the standard model unknown, level of hierachy of supersymmetry. We are assuming that the supersymmetry has a symmetry that is hierachial higher than that of the compound, U (1) Ø SU (2) Ø SU(3), of the standard model. Our symmetry is representing all four forces by just one group. We depart from Einstein’s equation where its basic metric is a four dimensional sphere (Table 1).
| Order (Dimension) | Signum | Number elements | Permutations |
| 1 | 1 | 1 | 1 |
| 2 | -1 | 6 | (12); (13); (14) |
| (23); (24); (34) | |||
| 2 | 1 | 3 | (12) (34); (13) (24) |
| (14) (23) | |||
| 3 | 1 | 8 | (123) (132) |
| (124) (142) | |||
| (134) (143) | |||
| (234) (243) | |||
| 4 | -1 | 6 | (1234) (1243) |
| (1423) (1432) | |||
| (1324) (1341) |
Table 1: Our symmetry group is the permutation group in four dimensions S4.
We depart from the metric being the four dimensional sphere, i.e.:
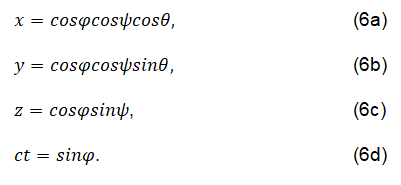
We use Einstein’s equation:
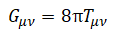
Our Einstein equation to solve is:
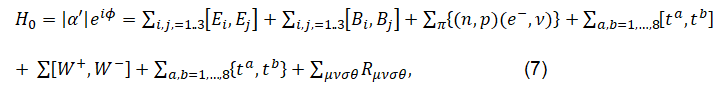
Where Rμ νσθ is made by Christoffel symbols. And with:
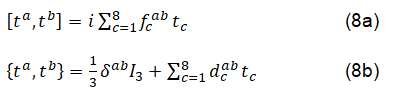
The l.h.s is the Higgs. The equation of the Riemann tensor is the following:
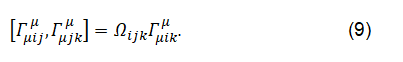
From the table of the permutation group we got: The Riemann tensor is ten dimensional. It contains four spacetime dimensions and six additional dimensions, which form the non-diagonal space of generators, i.e., Γij,i,j=1, …,3.
The non-diagonal parts are dual like the electric and magnetic field of the Faraday tensor. Thus instead of twelve non diagonal generators we got six. The trace defines a Clifford torus. The Clifford torus is given by a product of two circles parametrized in two dimensions by S1 ∈ (0,2 π), i.e.,
S1=(cos φ, sin φ), φ ∈ (0,2 π). (10)
S1 ⊕ S1=S2 ∈ R4. (11)
The overall geometrical value is becoming S1 ⊕ S1=2πr+2πr=4πr.
The fermionic particles are involved in our equations following anticommutation rules. But the neutron has a special role. Its antiparticle is just the neutron itself. The equation is:
n+ν=p+e- (12)
The proton, the electron and the neutrino are having antiparticles, are for now four dimensional spinors:
{Sij,Sjk }=εijk Sik, Sij=σi⊕σj. (13)
The fermions are forming commutation relations with the bosons.
The three dimensional sphere, our point of departure is compactified to a two dimensional plane with a north pole. This is done by a stereographic projection. The stereographic projection on a plane through a specific point, the center, perpendicular to the diameter through the point. The result is a two dimensional compact plane surrounded by a circle filled with points. Spacetime is compactified to a two dimensional disc, where we are examining the conformal Moebius transformation as symmetry transformation.
Departing from the two dimensional system,
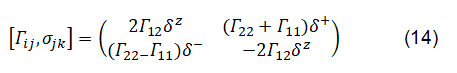
The compactified plane is given by Γ=π•r2. Thus
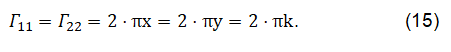
Comparing with (6) we receive:
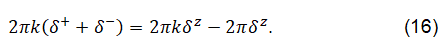
Translating to our system, we are receiving:
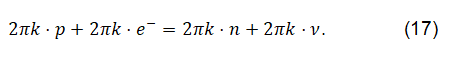
The whole system, Clifford torus plus our two dimensional disc has an overall geometrical value, that is 4πl ⊕ 2πk=8π(l+k). That means geometrically the entities, Clifford torus and the weak interaction are carrying a complex graviton, since 8π is the signature of a graviton. The combination of the Clifford torus and the plane is orientated. This is interpreted as the direction of spin.
Discussion
We were examining a system that contains all four forces. Gravity is incoporated by an D=11 dimensional term. The eleventh dimension is the dilaton, which is the additional dimension of the internal six dimensions. Thus our theortical ansatz is a M-theory. The internal dimensions were compactified. The 4-d spacetime are regarded as a Clifford torus, i.e., S1 ⊕ S1=S2 ∈ R4. The geometrical measure of the Clifford torus is A=2πr ⊕ 2πr=4•πr. We have identified the dilaton as a scalar, which is interpreted as the part of a Higgs at higher energy. The dilaton is responsible for the quantisation of the Higgs and thus of the whole parts of Einstein’s equation:
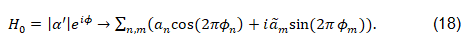
By
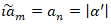
The Higgs follows:
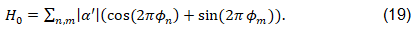
Since the Higgs is quantized all other fields are quantized. Einstein’s equation is now:
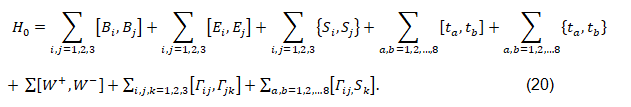
We have presented a N=2,D=4 theory, that is based on the permutation group S4. The permutation group is representing all four forces. The product of three groups of the standard model works heuristically. In our theory, the four forces are described by one group S4.
Our solution shows conformal invariance. The result of Γμνστ, is a Clifford torus linked to a plane encompassed by a circle with geometrical result of Ω=8•π, which is identified geometrically as the value of the graviton.
We were examining conformal duality. That is:
z'=α'/z. (21)
In polar coordinates with z'= it follows that:

Thus α'=(m2). What is conformal invariance? Exactly (22). We are coming back to the example of a circle. A circle, whose radius has been expanded at one point has been shrinked at a point perpendicular to the former, becomes an ellipsis. An ellipsis is still conformal in the sense that α'>1.
Thus,

With β is a scalar.
Back to Equation 19. If we identify the cosine with the Gaussian curvature and the sine with the geodetic curvature, we are receiving:
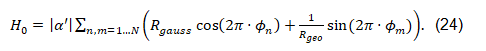
References
- Nambu Y. Quark model and the factorization of the Veneziano amplitude. Broken symmetry: Selected papers of Y. Nambu. 1995;13:258-67.
- Nielsen HB. An almost physical interpretation of the dual N point function. Nordita report, unpublished. 1969.
- Susskind L. Harmonic-oscillator analogy for the veneziano model. Phys Rev Let. 1969 23(10):545.
- Susskind L. Structure of hadrons implied by duality. Phys Rev D. 1970 1(4):1182.
- Ramond P. Dual theory for free fermions. Phys Rev D. 1971;3(10):2415.
- Neveu A, Schwarz JH. Tachyon-free dual model with a positive-intercept trajectory. Phys Lett B. 1971;34(6):517-8.
- Scherk J, Schwarz JH. Dual models for non-hadrons. Nuclear Phys B. 1974;81(1):118-44.
- Yoneya T. Connection of dual models to electrodynamics and gravidynamics. Prog Theor Phys. 1974;51(6):1907-20.
- Das SR. Degrees of freedom in two dimensional string theory. Nuclear Phys B-Proceed Suppl. 1996;45(2-3):224-33.
- Schwarz JH. An SL (2, Z) multiplet of type IIB superstrings. Phys Lett B. 1995;360(1-2):13-8.
- Palan P. Duality in statistical mechanics and string theory. Phys Rev Lett. 1987;58(16):1597-9.
- Witten E. Five-branes and M-theory on an orbifold. Nuclear Phys B. 1996;463(2-3):383-97.
- Vafa C. Evidence for F-theory. Nuclear Phys B. 1996;469(3):403-15.
- Kay Zum Felde. Higgs boson and the evolution of the universe derived from einstein’s equation with a fourdimensional sphere as the metric. J Pure Appl Math. 2023;7(5).291-6
- Green MB, Schwarz JH. Anomaly cancellations in supersymmetric D=10 gauge theory and superstring theory. Phys Lett B. 1984;149(1-3):117-22.
- Frampton PH, Kephart TW. Explicit evaluation of anomalies in higher dimensions. Phys Rev Lett. 1983;50(18):1343.
- Witten E. String theory dynamics in various dimensions. Nuclear Phys B. 1995;443(1-2):85-126.
- Felde KZ. Analysis of the four dimensional sphere being metric of Einstein’s equation. J Pure Appl Math. 2023;7(4):225-6.






