Mathematical analysis of the transmission dynamics of syphilis in china

Tiantian Zhao; Zhipei Zhang; Haiyan Jiao; Ying Liao

doi:10.37532/2752-8081.23.7(1).32-36

Tiantian Zhao^*, Zhipei Zhang, Haiyan Jiao and Ying Liao

Division of Infection Prevention and Control, Puyang People's Hospital, Puyang, 457001, China, Email: zhaott0212@163.com

^*Correspondence: Tiantian Zhao, Division of Infection Prevention and Control, Puyang People's Hospital, Puyang, 457001, China, Email: zhaott0212@163.com

Received: 13-Jan-2023, Manuscript No. puljpam-23-6050; Editor assigned: 14-Jan-2023, Pre QC No. puljpam-23-6050 (PQ); Accepted Date: Jan 19, 2023; Reviewed: 17-Jan-2023 QC No. puljpam-23-6050 (Q); Revised: 18-Jan-2023, Manuscript No. puljpam-23-6050 (R); Published: 30-Jan-2023, DOI: 10.37532/2752-8081.23.7(1).32-36

Citation: Zhao T, Zhang Z, Jiao H, et al. Mathematical analysis of the transmission dynamics of syphilis in china. J Pure Appl Math. 2023; 7(1):32-36.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

Background: Syphilis, a sexually transmitted infectious disease caused by the bacterium treponema pallidum， and it remains a significant cause of morbidity in many developing countries. Mathematical models of the transmission dynamics of sexually transmitted infections have provided insights of relevance both to the interpretation of observed epidemiological patterns and to the design of control programs.

Goal and study design: Based on the syphilis data in China from 2010 to 2020, the SEIRS dynamical model was established to provide theoretical support and quantitative basis for syphilis control in China.

Results: First of all, based on the data of syphilis in China from 2010 to 2020, the parameterizations and model calibration are carried out. The fitting results are in good agreement with the data. And then, we calculate the basic reproduction number R₀, and R₀=1.0556, which means that the syphilis epidemic will continue to be prevalent in China. Moreover, sensitivity analysis shows that the progression rate from incubating to infection (w), treatment rate in infection stage (γ), and treatment rate in incubating stage (α) play a critical role in mitigating the syphilis outbreaks.

Conclusion: These results can help us gain insights into the epidemiology of syphilis and provide guidance for the public health authorities to implement health education programs.

Keywords

Transmission Dynamics; Epidemiological patterns; Dynamical model; Mathematical models

Introduction

Syphilis is a sexually transmitted infection caused by the bacterium Treponema pallidum. According to the World Health Organisation (WHO), 710 million persons have been infected with syphilis [1]. Also, syphilis remains a serious public health problem in China. In 2020, about 464,435 people were infected with syphilis, and prevalence and mortality were 33.0831/100,000, 0.0038/100,000, respectively [2].

Over the years, some mathematical models have been developed to describe the population dynamics of syphilis. For example, Garnett et al. built a mathematical model that includes the basic stages of the disease and assumed that infected individuals acquire temporary immunity only after recovery from the latent and tertiary infections [3]. Grassly et al. established an S-I-R-S model for syphilis using data for the USA from 1941 to 2002 [4]. Tuite et al. developed a risk-structured deterministic compartmental mathematical model of syphilis transmission in a population of sexually active MSM [5]. Iboi et al. rigorously formulated and analysed a mathematical model for syphilis transmission that includes the early and late latent stages of syphilis infection, reversions of early latent syphilis to the primary and secondary stages as well as the three potential outcomes emanating from the late latent stage of infection [6]. Okuonghae et al. built and analysed a new multi-stage deterministic model for the transmission dynamics of syphilis, which incorporates disease transmission by individuals in the early latent stage of syphilis infection and the reversions of early latent syphilis to the primary and secondary stages [7]. Nwankwo et al. investigated the synergistic interaction between HIV and syphilis using a mathematical model that assessed the impact of syphilis treatment on the dynamics of syphilis and HIV co-infection in a human population where HIV treatment is not readily available or accessible to HIV-infected individuals [8]. Feldman et al. conducted a theoretical analysis of a generic S-I-S system with reinfection followed by numerical simulations of a more complex model to capture the natural history of untreated and treated syphilis [9]. While the work by Jing et al. developed a multiple-stage S-I-R-S epidemic model taking into account the public health awareness and behaviors of syphilis [10].

Motivated by the above works, in this paper, we established an S-E-IR- S model for syphilis using data for the China from 2010 to 2020, and calculated the basic reproduction number R0. Further, to provide theoretical support and quantitative basis for the prevention and treatment of syphilis in China.

Materials and Method

Data

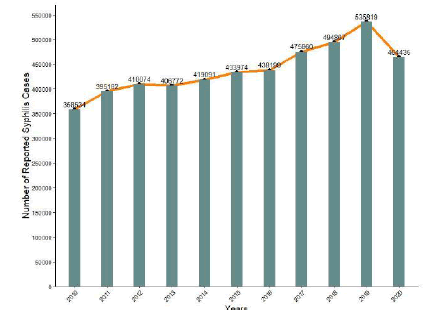
The syphilis cumulative cases in China from 2010 to 2020 were obtained from the National Bureau of Statistics(NBS) See Figure 1.

Figure 1: The syphilis cumulative cases in China from 2010 to 2020

Formulation of Mathematical Model

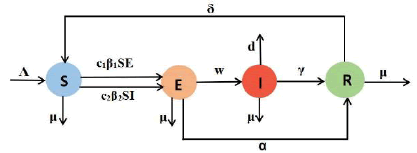
The total sexually active population at time t is denoted by N(t), and it is divided into four mutually exclusive compartments, so that:

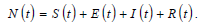
equation

Let S(t) denote the number of individuals who are susceptible to syphilis at time t. E(t) represent the number of exposed individuals (i.e., newly-infected individuals who have not yet shown clinical symptoms of the disease). I(t) indicate the number of infected individuals. And, R(t) is the number of recovered individuals at time t.

According to the flowchart in Figure 2, the syphilis transmission model is given as follows:

Figure 2: The flow chart of syphilis transmission

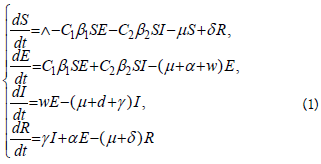
equation

All parameters are positive and the corresponding meanings are given in Table 1.

TABLE 1 Parameter values in model (1)

Symbol	Interpretation	Units	Value	Source
Λ	Recruitment rate of individuals	Number	10010000	fitting
μ	Nature death rate	Number	0.00709	Adapted from China Statistical Yearbook(2021)
d	Death rate due to disease	Number	0.0001393	Adapted from China Statistical Yearbook(2021)
c₁	Rate of sexual partner change with incubating	Sexual partners per year	20	Garnett et al.(1997)
c₂	Rate of sexual partner change with infection	Sexual partners per year	20	Garnett et al.(1997)
b₁	Transmission probability from incubating	Per sexual partnership	0.1211×10^-7	fitting
b₂	Transmission probability from incubating	Per sexual partnership	0.2691×10^-7	fitting
w	Progression rate from incubating to infection	per year	0.13	Nwankwo and Okuonghae(2018)
γ	Treatment rate in infection stage	per year	0.8	Adapted from CDC(2021) and Syphilis.
α	Treatment rate in infection stage	per year	0.9626	Adapted from CDC(2021) and Syphilis.
δ	Relapse rate of recovered return to susceptible sub-population	per year	1.6590×10^-6	Jing et al.(2021)

Model analysis

The basic reproduction number R0, one important threshold quantity to determine whether an epidemic will spread or die out, is defined as the expected number of secondary cases produced by one infected person during its infectious period in a completely susceptible population [11]. Notice that 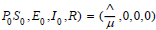equation is the disease-free equilibrium of model (1), where 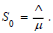Following the next generation matrix methods [12], we can define that

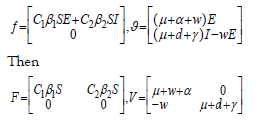
equation

Then, we can calculate that

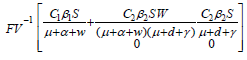
equation

The basic reproduction number of model (1) is the largest eigenvalue of the matrix FV^-1 , that is

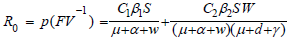
equation

Result

Model calibration

According to existing literature, we can estimate the parameters whose values are given in Table 1. The detailed estimation process of the parameter values are as follows:

a) From the statistic results of China population statistic yearbook during 2010-2020, we obtain the mean of natural death rate(μ) is 7.09 of the whole population.

b) The initial data of model (1) are S(0) = 1411780000, E(0) = 3000000, I(0) = 358534, R(0) = 295000.

c) Using the population equation 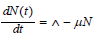and nonlinear least square method, we get ∧ =10010000.

d) Using of the parameters listed in Table 1 and model (1), we simulated the infectious number of syphilis from 2010 to 2020. The parameters β₁ and β₂ are obtained by the nonlinear Least-square method with the help of MATLAB tool fminsearch.

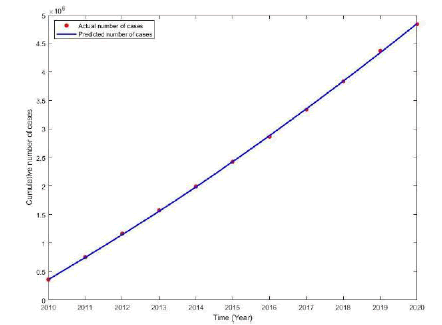
Figure 3 shows the fitted result of model (1) with the syphilis infected data from 2010 to 2020 in China. Obviously, model (1) fits the actual data very well in general.

Figure 3: The fitted result of model (1) with the syphilis infected data from 2010 to 2020 in China. And The solid red dots and blue solid lines indicate the actual and fitted cumulative number of syphilis cases, respectively

Sensitivity analysis

Uncertainty and sensitivity analysis are necessary to explore the behavior of many complex models, since the structural complexity of models are coupled with a high degree of uncertainty in estimating the values of many input parameters. In this section, Latin Hypercube Sampling (LHS) and Partial Rank Correlation Coefficient (PRCC) were used to to quantify the impacts of each parameter in model (1).

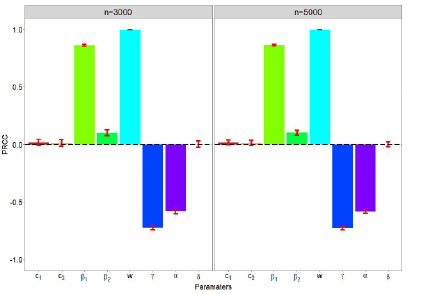
And the PRCC and P values were calculated by sampling n=3000 and n=5000, respectively. With the simulated parameter values and the data of syphilis from 2010 to 2020 in China, we can obtain the numerical distribution of the basic reproduction number R0=1.0556. According to the threshold theory, the disease will not disappear in a short period of time in China [13-15].

Consider the influence of parameter c₁, c₂, β₁, β₂, w, γ, α, δ of model (1) on the basic regeneration number R₀ (See Figure 4). The PRCC of the estimated parameters with respect to R₀ are showed in Table 2. Table 2 and Figure 4 show the exact PRCC and p values of each input parameter and the effect on the basic reproduction number R0, respectively. We assume the significance level α<0.05. The larger the absolute value of PRCC, the stronger the correlation between the input parameters and R₀. It can be seen from Table 2 that only β₁, β₂, w, γ and α have significant impact on R₀. More concretely, parameters γ and α have positive impact on R0 and parameters β₁, β₂ and w have negative impact.

TABLE 2 Partial Rank Correlation Coefficients (PRCCs) for R₀ on each input parameter variable

Parameters	n=3000		n=5000
Parameters	PRCC	P-value	PRCC	P-value
c₁	0.0122	0.5063	0.0158	0.3365
c₂	0.0135	0.4615	0.0116	0.4085
β₁	0.7521	<0.001	0.8653	<0.001
β₂	0.1956	<0.001	0.1013	<0.001
w	0.9974	<0.001	0.999	<0.001
γ	-0.7595	<0.001	-0.7298	<0.001
α	-0.7883	<0.001	-0.5841	<0.001
δ	-0.0162	0.3765	-0.0001	0.5018

Figure 4: Partial Rank Correlation Coefficient (PRCC) results for the dependence of R₀ on each parameter

Assessment of control strategies

In this subsection, we further investigate the impacts of various control strategies on reducing the spread of syphilis in China. Based on the validated parameters listed in Table 1, we carry out the following numerical simulations to explore the control strategies on the infected number.

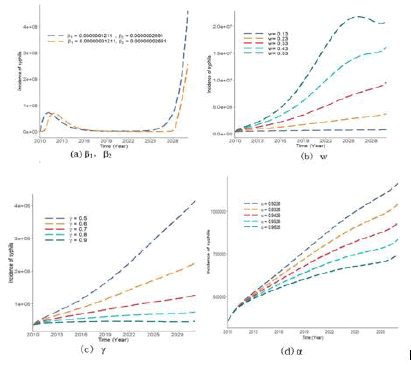
In Figure 5, Based on the dynamics of the total number of syphilis infections, we study the transmission probability β₁, β₂ from incubating and infection syphilis, the progression rate from incubating to infection of syphilis w, the treatment rate in infection stage of syphilis γ, and treatment rate in incubating stage of syphilis α, respectively.

Figure 5 (a) demonstrates that the probability of transmission will not alter the simulation results significantly, even if we replace the values for β₁ and β₂. Figure 5 (b) shows that the infectious number of syphilis is increasing significantly when the progression rate from incubating to infection of syphilis w increases from 0.13 to 0.53. Figure 5 (c) indicates that γ increasing (the treatment rate in infection stage of syphilis) from 0.5 to 0.9, fewer susceptible population will be infected by syphilis. And Figure 5 (d) represents that α (the treatment rate in incubating stage of syphilis) increasing from 0.9226 to 0.9626, the infected number of syphilis is decreasing.

Figure 5: Sensitivity of the solutions of model (1) with respect to parameters β₁, β₂, w, γ and α. (a). Time variation of infectious cases for two different sets of parameters. β₁ and β₂ correspond to the probability of transmission of infection during one partnership to a person from his/her partner with incubating and infection syphilis, respectively. For the orange curve we used our baseline parameters, shown in Table 1. (b). The infectious number of syphilis under migration strategy of increasing w from 0.13 to 0.53; (c) under migration strategy of increasing γ from 0.5 to 0.9; (d) under migration strategy of increasing α from 0.9226 to 0.9626, respectively

Conclusion and Discussion

In face of health threat posed by increasing syphilis worldwide, WHO have publicized plans to eliminate syphilis actively and set syphilis reduction targets for 2030. We have attempted to define a simple mathematical framework for the study of the transmission dynamics of treponema pallidum and to use this to identify the key parameters and processes that determine observed epidemiological patterns.

In this paper, we develop a SEIRS epidemic model considering the relapse rate of recovered return to susceptible sub-population of syphilis. The basic reproduction number R₀ of the model is calculated. As we know, if R₀<1, the disease-free equilibrium is globally asymptotically stable, then syphilis epidemic could be controlled. On the other hand, if R₀>1, the syphilis epidemic will continue to be prevalent.

Based on the data of syphilis in China from 2010 to 2020, the parameterizations and model calibration are carried out. The numerical solution of model (1) is in close agreement with the data (as shown in Figure 3). The basic reproduction number of syphilis is estimated to be approximately R0=1.0556. The sensitivity analysis of parameters with respect to R₀ shows that the transmission probability β1, β2 from incubating and infection syphilis, progression rate from incubating to infection of syphilis w, treatment rate in infection stage of syphilis γ, and treatment rate in incubating stage of syphilis α play an important role in mitigating the syphilis outbreaks. We then explore the impact of various control strategies on reducing the infected number of syphilis, that is, decreasing w, increasing γ, and increasing α, respectively. Since the singular implementation of any one strategy discussed above may be not sufficient to effectively control syphilis at the population-level (as shown in Figure 5), the joint control strategy is more effective to reduce the infectious number of syphilis at a more attainable level. These results can help us understand the epidemiology of syphilis and provide guidance for the public health authorities to implement health education programs.

This study also has several limitations: Firstly, Mathematical models are theoretical means of producing caricatures of real phenomena. In order to simplify our model, we defined the primary syphilis, secondary syphilis and tertiary syphilis as syphilis infected individuals. It suggests that we need for more work to develop a multiple-stage S-E-I-R-S model taking into account more parameters of syphilis. Secondly, whereas we tested many scenarios by varying all the parameters in our model. The results underline the importance of different behavioral patterns in the study of the target population. But we need to consider more intervention strategies, such as public health awareness and notification strategies. Thirdly, development of a syphilis vaccine would be a potential promising step towards control. With the development of economy, whereas it is worth to consider this issue in future.

Acknowledgements

The authors thank to the assistance from editors.

Author Contributions

Tiantian Zhao drafted the article, conducted data analysis and led the writing of the paper. Zhipei Zhang, Haiyan Jiao and Ying Liao conducted data analysis and discussed the data and perspectives. All authors provided contributions to the paper and approved the final version.

Data Availability Statement

Syphilis data to this article can be found online at http://www.stats.gov.cn/tjsj/ndsj/.

Declaration of Competing Interest

The authors declare that there is no conflict of interests regarding the publication of this paper. All authors read and agree to submit this manuscript to your journal.