Möbius and simple loop strips as 2D topological spacetime structures of preonic fermions and bosons

Received: 06-Jun-2023, Manuscript No. puljmap-23-6507; Editor assigned: 08-Jun-2023, Pre QC No. puljmap-23-6507 (PQ); Accepted Date: Jun 29, 2023; Reviewed: 15-Jun-2023 QC No. puljmap-23-6507 (Q); Revised: 23-Jun-2023, Manuscript No. puljmap-23-6507 (R); Published: 10-Jul-2023, DOI: 10.37532.2023.6.3.1-8

Citation: Tang J., Tang B., Tang Q. Mobius and simple loop strips as 2D topological space-time structures of preonic fermions and bosons. J Mod Appl Phys. 2023; 6(3):1-7.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

This work presents a model to treat the relativistic quantum dynamics of particles in a 2D Minkowski spacetime. Using independent 2x2 real-value matrices to represent a time-shift operator E, a space-shift operator P, and a mass operator M, we first derive and show these exist only two types of operator equations, representing a bosonic preon for the symmetric type-I case with commutative E and P, and a fermionic preon for the anti-symmetric type-II case with an anti-commutative relation. We illustrate their topological differences and show that the wave during propagation of the type-II preon as a Weyl-fermion exhibits a twist like a Mobius strip. In contrast, the type-I bosonic preon behaves like a simple loop strip without a twist. We have also examined the case with a rest mass for a 2D particle and a Dirac particle in 4D. Unlike the conventional string theories, our model consists of two fundamental structures, a Mobius-strip fermionic preon, and a simple-loop bosonic preon. These two topological preonic structures can be used as the most fundamental building blocks for constructing elementary particles of higher dimensions.

Key Words

Preons; Mobius strip; Open-loop strips; Fermions; Bosons; Standard Model; String theory; Weyl fermion; Dirac equation

Introduction

Relativity and quantum mechanics have been the two major pillars for modern physics since the dawn of the last century [1,2]. They are the most successful physics theories in human history and their predictions have been put to test with unprecedented accuracy. However, there remain many puzzling mysteries, including some counter-intuitive quantum phenomena such as quantum entanglement, double-slit self-interference of single particles, the collapse of a wave function during measurements absence of righthand neutrinos, the mass oscillations of neutrinos, the causes of three generations of quarks and leptons, the physical origin of the Standard Model, dark matter, dark energy, and quantization of gravity, etc. [3- 15]. In this work, we aim to improve our understanding of the spacetime fabric, its topological structures, and their effects on relativistic quantum fields and particles. We provide a topological analysis of structural deformations as represented by excited quantum fields and particles in a 2D Minkowski spacetime [16,17].

Our analysis is in 2D instead of the actual 4D case, to increase mathematical simplicity while still retaining the core concepts of physics. We present a dual-component model to describe the relativistic quantum dynamics of elementary particles. We will show how this model will naturally lead to the existence of only two kinds of elementary field excitations: fermions with a Mobius strip structure, and bosons with a simple loop structure. We will also elucidate the concepts behind Pauli’s exclusion principle, fermionic statistics, and bosonic statistics a Mobius strip.

Theory

In Newtonian mechanics or Einstein’s special relativity, the dynamics of a particle are vastly different from the motion of electromagnetic waves or other types of waves governed by.

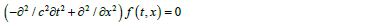
To unite the realms of particles and waves, a model with a dualcomponent real-value wave function is necessary to describe the quantum behavior of particles. The model is based on de Broglie’s particle-wave duality and Einstein’s mass-energy relation

for a particle with a rest mass For a massless particle, we first consider a wave function of a dual-component wave function

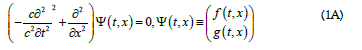
or equivalently after Fourier transform,

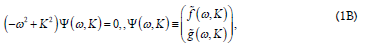
where a natural unit of 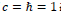is used in this work [18]. A Fourier transform of the above equation leads to a 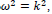relation between the frequency and the wave vector This dispersion relation is equivalent 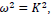to according to 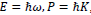or 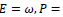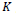, expressed in natural units, of Einstein’s energy relation to momentum for a massless particle, and de Broglie’s particle-wave duality postulate [14]. Eq. (1A) can be expressed in an operator form

Here we use Dirac’s ket-vector notation 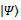to represent a 2x1 column vector of the Fourier-transformed wave function. 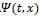Eq. (1B) can be met if

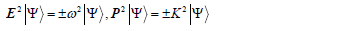
After close examination of Eq. (1C) and the requirement of its Lorentz invariance, we have found exactly two types of solutions exist. For the type-I solution of

one has a commutative relation 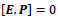and

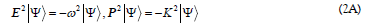
Or

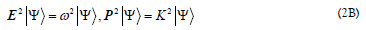
For the type-II solution of 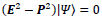one has a noncommutative relation with 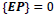and

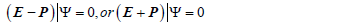
These two types of solutions have different physical properties and distinctive topological structures. Because 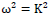we can normalize 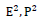to become dimensionless operators and we will use this convention for the case of a massless particle.

Before we solve the operator equation in Eq. (1B) and assign these two operators to 2x2 real-value matrices, or equivalently, converting the 2^nd-order differential equation in Eq. (1A) involving a dualcomponent wave function into a set of linearly coupled 1^st order differential equations, we shall examine the Lorentz transform between a fixed frame and a moving frame. According to special relativity theory, the Lorentz boost for a moving reference frame traveling along the x-axis is given in natural units by [18,19]

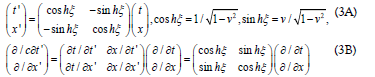
From the above equation, the time-shift and space-shift operators 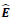and 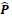at the moving frame become

Based on Eq. (3C) one obtain

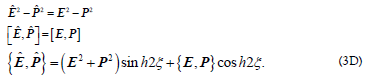
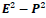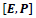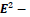
which confirms that and are Lorentz invariants, but are not. Therefore, for type-I particles the wave equation 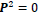and the commutative relation 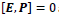are satisfied and invariant under a Lorentz boost.

However, for type-II particles with an anti-commutative relation 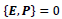one has In addition, one also has 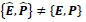which is not Lorentz invariant if one uses the Lorentz boost matrix of Eq. (3C). In order for 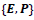to be Lorentz invariant one needs to generalize the transformation matrix for the type-II case by

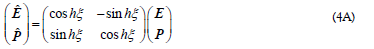
From Eq. (4A), one obtains the invariance of the anti-commutator

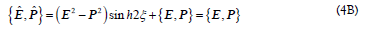
because 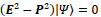for type-II particle. Therefore, both 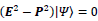and 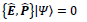are indeed invariant under the Lorentz boost using Eq. (4A). Based on the above analysis, we conclude an important finding: the Lorentz boost matrix for type-I particles in Eq. (3C) are different from that in Eq. (4A) for type-II particles, which therefore must be different from type-I particles. One can also define time and space operators T and X with T 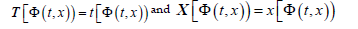respectively.

According to Einstein’s special relativity,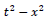 is an invariant under a Lorentz transform? Likewise, in the operator formalism is also an invariant similar 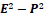to Therefore, one also has two solutions – a commutative type-I with 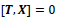and an anticommutative type-II with 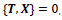just like E and P

Together with our previous definition of 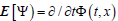and 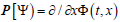we can express these two types of Lorentz boosts for the transformation for the 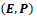and 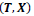pairs using 2x2 real-value matrices. For type-I scalar particles, one has

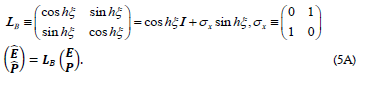
One can show the following commutative relations are invariant under the Lorentz boost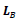

As a reminder, in this work we only use real-value operators or wave functions, so the appearance of these commutators differ slightly from the conventional definition of the operators that involve a pure imaginary number. For type-II spinor particles, one has

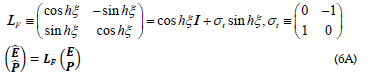
The Lorentz boost matrix shown above for type-II particles is different from those for type-I particles. The commonly used Lorentz boost matrix in literature is only valid for type-I scalar particles where E and p commute. Such a notion has not been reported in literature. Using the above equation one can show the following commutative relations are invariant under the Lorentz boost:

It is important to point out that if the traditional Lorentz boost 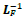were used instead 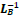for T and X, those commutative relations would no longer be Lorentz invariant.

Now we discuss specific assignments for the operators in both type-I and type-II cases. For the type-I case with 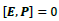and 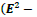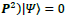which are proven to follow the Lorentz boost of Eq. (3C), we first consider the choice of 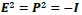would lead to flip-flop oscillations of the f and g components in spacetime. One can assign these 2x2 real-value matrix operators to

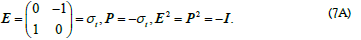
Using the above operator assignment in the frequency-wave vector domain, or the corresponding partial derivatives 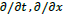in the time-space domain, one can express the wave equation explicitly as

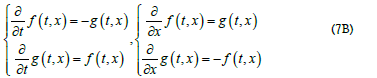
Eq. (3B) exhibits swapping behavior between f and g along both the time and space axes. The topological structure of the above coupling scheme is illustrated in Figure 1a, displaying clockwise rotation of f and g (with red and blue arrows) around four quadrants as time evolves. Conversely, as space evolves the rotation is counterclockwise originally from the 1st quadrant to the 2nd quadrant. The solution of Eq. (3B) with 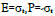corresponds to a spiral wave with a righthand chirality along the x-axis. If one assigns 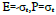with governing equation given by

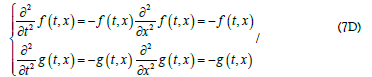
one can show both Eqs. (7B) and (7C) lead to

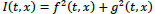
Both Eqs. (7B) and (7C) satisfy the conservation of the intensity 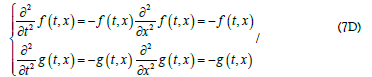in time and space

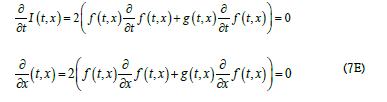
According to Eq. (7C), the quadrant rotates counterclockwise along the time axis but clockwise along the x axis as shown in Figure 1b, and the spiral wave propagation has a left-hand chirality. For the other choice of E² = P² = 1, there exist two possible assignments

i.e., 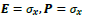and 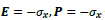where 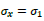is the first Pauli 2x2 matrix where we define 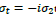to avoid the use of an imaginary number, which might cause some confusion. While there is an isomorphism between the algebra of the dimensional vector space and the complex plane, in this work we are dealing with purely real-value wave functions and 2x2 matrix operators. One can show that for 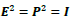the wave equations governed by and 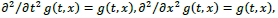an exponentially expanding or contracting amplitude. The topological representations of these two cases are illustrated in Figure 1c and Figure 1d, respectively. Therefore, the unphysical choice of 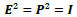cannot be used here.

Only Eq. (3B) with 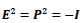an describe the flip-flop behavior for f and g across the lattice plane, as schematically illustrated in Figure 1 showing two types of possible flip-flop schemes

Figure 1: Topological 2D spacetime structures of the type-I particles. In subplot (a) for mode-1, according to the recursive scheme, the quadrant formed by f (red arrow) and g (blue arrow) rotates clockwise along the t-axis and counter-clockwise along the x-axis, representing left-hand chirality for the rotation viewing along the time axis. The diagonal dot line denotes the wave propagation along x â?? ct . For mode-2 in the subplot (b) it shows a reverse rotation direction for f and g, representing right-hand chirality. In subplots (c) and (d), their specific inversion or reflection exchange schemes between f and g lead to either contraction or expansion with exponentially decreasing or increasing amplitudes

One can obtain a plane-wave solution of 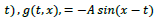as illustrated in Figure 2A. If one assigns 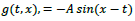instead, its plane-wave solution becomes 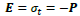The difference is in the propagation chirality. If one chooses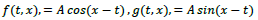 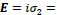the wave propagates along the reverse direction. For the other type-II solution of Eq. (2B) with 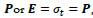one has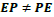

For the above equation to be satisfied, one has 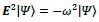and 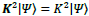Because of the special case of a massless particle 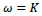we normalize the operators E and P to become unitlessoperators for simplicity. Therefore, one must have the following constraints

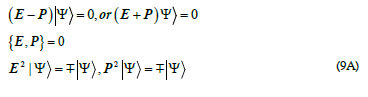
The above anti-commutative property between E and P for this typeII case is characteristically from the type-I case with commutative E and P . Based also on the condition of the wave function being real, one has the following assignment.

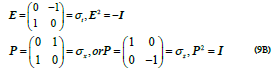
Using the above operator assignment, the wave equation for E =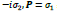

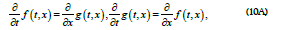
and for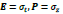

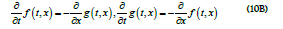
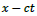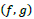The coupling scheme can be schematically illustrated in Figure 2, showing a binary exchange between the f and g components along the axi s. For mod the re is an alt ernate exc hange between and 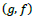like a Mobius strip¹⁵ betw een the f an d g components. The topological representation for these two types of wave propagation is illustrated in Figure 3. For mode-2, the process between 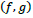and 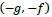rese mbles anot her type of a Mobius strip²⁰ twisting. Both above equations lead to the wave equation for each of the dual components

Figure 2: The topological structures for type-II spinor particles and their wave propagation along x-ct, exhibiting two modes of the intertwined dynamics like the twisting of a Mobius strip. (a) Mode-1 with a swapping between (F,G), representing partial derivatives in time and space for the top row and the bottom row, and (G,F). (b) Mode-2 with an exchange between (F,G) and ( ), meaning an inverse amplitude (-G,-F). (c) Mode-3 with an exchange between (F,G) and (G,F). (d) Mode-4 with an exchange between (F,G) and ( ) . The last two modes correspond to an exponentially decreasing or increasing amplitude.

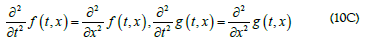
According to the analysis in this work, both type-I and type-II massless particles all travel at the speed of light. For the type-I particle, which represents a scalar particle, E and P are commutative; however, for the type-II particle, which has an intrinsic structure, E and P are anticommutative.

In the type-I case, the recursive relation does not involve direct coupling between time and space, while in the type-II case, the recursive relation involves an intertwined coupling between space and time like a Mobius strip as shown in Figure 3.

Figure 3: The topological structure representation of the antisymmetric typeII fermionic preon vs. the symmetric type-I bosonic preon. The fermionic preon has a topological structure like a Mobius strip, and possesses a half-spin, whereas the bosonic preon possesses a simple closed-loop strip. The operators E and P are time-shift and space-shift operators, respectively, and subscripts represent anti-symmetry (A) and symmetry (S) for the fermionic preon and bosonic preon, which could be used to construct other operators in 4D spacetime.

The equation of Eq. (4B) with the choice of 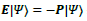in the continuum limit has a plane-wave solution as

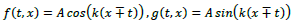which is 90- degrees out of phase as illustrated in Figure 4a. For the other choice of 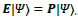its plane wave solution becomes

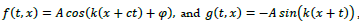indicating a wave propagating along the opposite x-axis or t-axis. The wave propagation for the type-I is shown in Figure 4a with the f and g components 90-degrees out of phase. In contrast, for the type-II case, the wave propagation is illustrated in Figure 4b, showing the f and g components in phase or 180-degrees out of phase. The plane-wave solutions of Eq. (6B) are given by

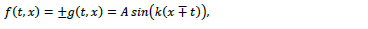
with the same phase or 180-degrees out of phase. The subplots shown in Figure 4c and 4d represent type-II wave propagation with f and g in-phase or 180-degrees out of phase. There also exist two modes, called L- and R-chirality depending on the relative phase relation between f and g.

Figure 4: Two types of wave propagation for the f and g components, each with two modes. (a) The wave propagation of the type-I waves with a chirality model L. The wave oscillations for f and g, 90-degrees out of phase, are along the x-axis. They are plotted orthogonal to each other for a better view, unlike an EM wave with the electric and magnetic fields along x and y. Depending on the recursive scheme, there exists a left-hand chirality and a right-hand chirality mode as shown in subplot (b). The subplots in (c) and (d) represent type-II wave propagation with F and g in-phase or 180-degrees out of phase. There also exist two modes, called L- and R-chirality depending on the relative phase relation between f and g.

The type-II particle described above represents a 2D half-spin massless particle, which is a 2D analogy of a 4D Weyl particle [20,21]. If one uses angular momentum operators of spin-1 particles instead of Pauli’s matrices in the treatment, the wave propagation of in-phase f and g components appear to be like the electric and magnetic field of a photon wave.

So far, we have considered type-I and type-II quantum lattice dynamics for massless particles. Let us now extend the treatment to particles with a rest mass. We first consider the rest frame, where there exists an internal oscillation with a frequency 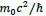dictated by its rest mass energy.

The wave equation in Eq. (1A) for a massless particle needs to be replaced by

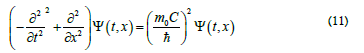
which is the Klein-Gordon equation in a discrete lattice. The above equation can be expressed in an operator form like Eq. (1B) but now with a mass term as

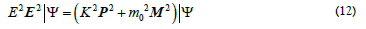
Eq. (7B) in natural units is equivalent to the de Broglie-Einstein relation of 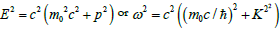satisfy the Pythagorean Theorem for 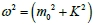Here we seek a solution for the type-II case that satisfies as an eigenvalue result of One can obtain a solution with if these operators satisfy

and To satisfy we can assign these operators to three anti-commutative 2x2 matrices as

The wave equation based on the above assigned operators, can be expressed explicitly by

A 2^nd kind of operator assignment of leads to

A 3^rd kind of operator assignment of leads tos

A 4th kind of operator assignment of leads to

Both above equations represent a massive half-spin particle, as a 2D analogy of Dirac’s equation for an electron in 4D spacetime. According to our analysis, there are four possible coupling schemes as illustrated in Figure 5, showing how the original massless spinor structures are coupled to the 2D Higgs fields with an attached spring. Such coupling leads to the spinless fermion acquiring its mass, slowing down the wave propagation from the speed of light.

Figure 5: Topological structures of spinor particles with a rest mass. There are four different coupling schemes between F and G, representing the dualcomponent wave function of type-2 particles. f and g represent the dualcomponent wave function of the spacetime fabric. The coupling of type-2 particles to the adjacent spacetime fabric causes the particles to acquire mass through the Higgs mechanism, but in 2D. Such couplings lead to a slower propagation velocity than the speed of light, owing to the nonlinear dispersion relation between the frequency and the wave vector.

The second possible solution, as an extension of the massless particle in the type-I case for a boson can be obtained if

Where,

In the above equation we need to use a tensor product of another 2x2 matrix to satisfy the constraints of and The above equations describe separate oscillations in time and space, unlike Eq. (8) which describes an intertwined link between partial differentials with respect to time and space. The third possible solution can be obtained if

Direct-products of two 2x2 matrices are required in order to satisfy the Klein-Gordon equation and these types of wave equations and solutions do not meet the constraints of the dualcomponent model with two real-value functions. Strictly speaking,Eq. (15B) with is the only qualified wave equation for a particle with a rest mass.

Before making a conclusion, it is worth pointing out the extension of our preon model to a Dirac electron. According to Dirac’s theory for the electron, using the gamma matrices, one has

where the natural unit is used. Equivalently, using the matrices and it can be expressed as Dirac’s1^st -order differential equation in spacetime leads to Einstein’s relativistic mass-energy relation in a natural unit. In Figure 6, we illustrate the topological structure of the antisymmetric type-II fermionic preon operators vs. the symmetric type-I bosonic preon in 4D spacetime. Unlike the 2D case with only one way to pair up the time and the space-derivatives, for a Dirac electron in 4D spacetime, the Dirac equation involves four gamma matrices, including a time-like operator and three space-like operators.

Figure 6: The topological structure representation of the antisymmetric typeII fermionic preon operators vs. the symmetric type-I bosonic preon in 4D spacetime. Unlike the 2D case in which there is only one way to pair up the time-derivative and the space-derivative, for a Dirac electron in 4D spacetime, the Dirac equation involves four gamma matrices, including a time-like operator and three space-like operators. Therefore, an electron has a highdimensional topological structure pf a fiber-bundle, with intertwined Mobius strips. The fermion-type preon operator has a topological structure like a Mobius strip, and possesses a spinor structure, whereas the boson-type preon operator possesses a simple closed-loop strip.

Therefore, an electron has a high-dimensional topological structure of a fiber-bundle, with intertwined Mobius strips , The fermionic preon operators has a topological structure like a Mobius strip, and possesses a spinor structure, whereas the bosonic preon possesses a simple closed-loop strip. One can generalize Dirac’s equation using hyper complex operators such as octonions to incorporate the extra degrees of freedom for leptons or quarks, which are assumed in the Standard Model to be a point-like object without a size. In the hyper complex operator formalism, such as quaternions, octonions or sedenions, all other operators are anti-commutative with each other, except the identity unit operator [22-23]. And all leptons or quarks should be regarded as particles with an internal structure and a finite size. Therefore, each pair of these operators could be regarded as a Mobius strip, and an elementary particle could be viewed as having a fiber-bundle structure like a higher dimensional Mobius structure [24].

Conclusion

In summary, we presented a dual-component model with two realvalue wave functions f and g to describe the relativistic quantum dynamics of fields/particles in a 2D Minkowski spacetime. Using an operator algebra approach with a time-shift operator E and a spaceshift operator P, together with another mass operator represented by three independent 2x2 real-value matrices, we can construct linearly coupled 1^st -order partial differential equations to describe the excitation and propagation of these quantum fields and their associated particles. We systematically analyzed all possible excitations of the 2D Minkowski spacetime fabric sheet that satisfy the de Broglie-Einstein relations between mass energy, frequency, and wave vector. From our analysis of all possible structural deformations, we have identified two types of solutions that satisfy the Lorentz invariance of

For a type-I massless bosonic preon, one has commutative relations of and for a type-II massless fermionic preon, one has anticommutative relations of This model leads naturally to only two kinds of field excitations and their associated particles as bosons and fermions. We shed light on the concepts behind Pauli’s exclusion principle, fermionic statistics, and bosonic statistics. We point out that spacetime itself consists of a dual-component fabric to allow the excitation and propagation of type-I bosonic preons and type-II fermionic preons. Unlike the conventional preon modes that encounter the mass paradox22, we have only two types of preons, antisymmetric fermionic and symmetric bosonic preons, both of which are massless. Our model also differs from the conventional string theory that invokes 1D string. Our model invokes the most fundamental unit with time-like and space-like 2D Mobius strips and simple-loop strips as building blocks of the actual elementary particles.

According to the history of the development of the conventional string theories, only 1D vibrating strings were considered, which could only account for boson excitations. The extension to fermionic excitation was made a decade later with the inclusion of supersymmetry. In contrast, our model consists of two most fundamental 2D spacetime structures, a Mobius-strip fermioni preon, and a simpleloop bosonic preon.

These two topological preonic structures can be used as the building blocks for construct of the known elementary particles of higher dimensions, in conjunction of the use of hyper-complex operators for the higher-dimensional spacetime. The Mobius strip and simple loop structures, which arise naturally from the wave equation as prescribed by Einstein’s special relativity and de Broglie’s wave-particle duality, could potentially be used as building blocks to construct actual particles in 4D, and to investigate the topological properties of elementary particles in the Standard Model. The extension of this 2D model to 4D spacetime and an inclusion of hyper complex operators as potential building blocks to construct elementary particles deserve further studies.

References

1. Mullarkey CA. Imaging and Sensing Applications with Atomic-Like Systems. Univ. Rochester; 2020.

   [Googlescholar]

2. Greiner W. Relativistic quantum mechanics. Springer, 2000.

   [Googlescholar]

3. Horodecki R, Horodecki P, Horodecki M, et al. Quantum entanglement. Rev. mod. phys. 2009; 81(2):865.

   [Googlescholar] [Crossref]

4. Erhard M, Krenn M, Zeilinger A. Advances in high-dimensional quantum entanglement. Nat. Rev. Phys.2020; 2(7):365-81.

   [Googlescholar] [Crossref]

5. Steeds J, Merli PG, Pozzi G, et al. The double-slit experiment with single electrons. Phys W. 2003; 16(5):20.

   [Googlescholar] [Crossref]

6. Zimmermann B, Rolles D, Langer B, et al. Localization and loss of coherence in molecular double-slit experiments. Nat Phys. 200; 4(8):649-55.

   [Googlescholar] [Crossref]

7. Marchewka A, Schuss Z. Measurement as absorption of Feynman trajectories: Collapse of the wave function can be avoided. Phys Rev A. 2002; 65(4):042112.

   [Googlescholar] [Crossref]

8. Liventsev D, Adachi I, Aihara H, et al. Search for heavy neutrinos at Belle. Phy Rev D. 2013; 87(7):071102.

   [Googlescholar] [Crossref]

9. Kajita T. Nobel Lecture: Discovery of atmospheric neutrino oscillations. Rev of M Phys. 2016; 88(3):030501.

   [Googlescholar] [Crossref]

10. Bilenky SM, Petcov ST. Massive neutrinos and neutrino oscillations. Rev of M Phys. 1987; 59(3):671.

    [Googlescholar] [Crossref]

11. Frampton PH, Hung PQ, Sher M. Quarks and leptons beyond the third generation. Phys R. 2000; 330(5-6):263-348.

    [Googlescholar] [Crossref]

12. Gaillard MK, Grannis PD, Sciulli FJ. The standard model of particle physics. Rev of M Phys. 1999; 71(2):S96.

    [Googlescholar] [Crossref]

13. Bertone G, Hooper D. History of dark matter. Rev of M Phys. 2018; 90(4):045002.

    [Googlescholar] [Crossref]

14. Chernin AD. Dark energy and universal antigravitation. Physics-Uspekhi. 2008; 51(3):253.

    [Googlescholar] [Crossref]

15. Nicolai H, Peeters K, Zamaklar M. Loop quantum gravity: an outside view. Class & Q Grav. 2005; 22(19):R193.

    [Googlescholar] [Crossref]

16. Catoni F, Boccaletti D, Cannata R, et al. Geometry of Minkowski space-time. Springer Sci. Bus. Media. 2011.

    [Googlescholar]

17. Stein H. On Einstein--Minkowski Space--Time. j. Philos. 1968; 65(1):5-23.

    [Googlescholar] [Crossref]

18. French AP. Special relativity. CRC Press; 2017.

    [Googlescholar]

19. Robertson HP. Postulate versus observation in the special theory of relativity. Rev of M Phys. 1949; 21(3):378.

    [Googlescholar] [Crossref]

20. Tanda S, Tsuneta T, Okajima Y, et al. A Möbius strip of single crystals. Nature. 2002; 417(6887):397-8.

    [Googlescholar] [Crossref]

21. Lutchyn RM, Sau JD, Sarma SD. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys rev letters. 2010; 105(7):077001.

    [Googlescholar] [Crossref]

22. D'Souza IA, Kalman CS. Preons: Models of leptons, quarks and gauge bosons as composite objects. World Scientific; 1992.

    [Googlescholar]

23. Dixon GM. Division Algebras: Octonions Quaternions Complex Numbers and the Algebraic Design of Physics. Springer Sci. Bus. Media; 2013.

    [Googlescholar]

24. Avrin, J.S., A Visualizable Presentation of the elementary particles,  J. Knot Theory Ramif.1793-6527.