Standard model of a binary digit of memory with multiple covalent modifications in a cell
Received: 30-Jan-2018 Accepted Date: Feb 09, 2018; Published: 13-Feb-2018, DOI: 10.37532/2752-8081.18.2.3
Citation: Ohnishi I. Standard model of a binary digit of memory with multiple covalent modifications in a cell. J Pur Appl Math. 2018;2(1):5-11.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
A model system of ordinary differential equations describing cyanobacteria’s circadian rhythm by use of a binary digit of memory induced by multiple covalent modification in a cell level is considered. It is mathematically rigorously proved that this system possesses bifurcation structure of hysteresis type in 1-site model. We apply it to the cyanobacterial circadian rhythm to make comparisons between some important biochemical experimental results and our simulations. These show very good agreement to elucidate theoretically fine skeleton structure with memory reinforcement effect in cell level.
Keywords
Cyanobacteria’s circadian rhythm; Binary digit of memory; Multiple covalent modification; Cell level; Bifurcation structure
LIfe can be considered to be a complex, but delicate, sensitive, and efficient system of organism obtaining high reproducibility and high evolvability in order to grow up, to undergo metabolic change, to react to stimulation, to control its feature, and so forth. For embodying these purposes, it is important to memorize and to communicate information on the past about themselves as precisely as possible. An organism can survive more stably, if the memorization is more correctly and more steadily, and if the communication is more rapidly. It is considered that these characters must be realized by a combination of some biochemical reactions. Especially, it is important how a strage element is constructed in a cell. In this paper we propose a kind of standard structure of mathematical model constructing a binary digit of storage element in a cell by use of covalent modifications and analyse it to elucidate its characteristic and important properties.
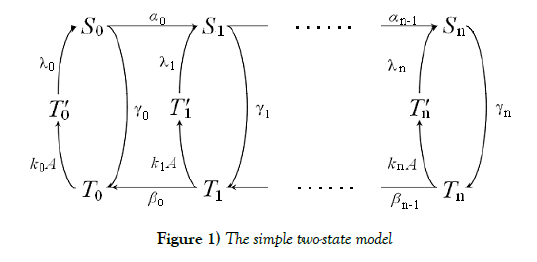
We consider a simple two-state (S and T ) model for receptor proteins. This is based on and is modified the model a little in the classical work of Professors S. Asakura and H. Honda [1], where they have originally considered about the problem of temporary reaction and postadaptation process in a cell. T stands for a state which has accepted attractants and is likely to take a convalent modifier, and T stands for the opposite state. S receives convalent modifiers one by one in a definite order, while S releases them in the reverse order. There are n possibly modifying sites receiving convalent modifiers in a receptor protein. Here we assume that a very rapid equilibrium of S and T is realized according to the mass-action law. We change some of important parameters’ directions to get a kind of hysterically switching structure of steady states, which is a foundation on the desirable storage element. In fact, the receptor protein constructs a binary digit in such a way that a state taking more convalent modifiers than a threshold number is regarded as \1”, the inverse state as \0”. In order to realize it, there must be a kind of bistability and hysterically switching mechanism of the system. In order to get this desirable nature, we adjust paramerers in the system in which the equilibrium between S and T goes to S side more, when the receptor protein has more convalent modifiers, and vice versa. This can make a state changing hysterically according to quantity of attractants, and as a result, it can make a digitally switching function robustly.
One of our important and interesting points is a correlation between the number of the possibly modifying sites and a kind of stability of the storage element. We therefore investigate how the width of hysteresis range varies, as the number of the sites becomes larger. The result is that the wider the hysteresis range is, the bigger the number is. Thus it is considered that the existence of a lot of sites contributes the stability of the storage element.
In order to verify usefulness of this fact more concretely, for example, later in § 3, we apply this model [2] to the phosphorylation–dephosphorylation circadian rhythm of clock proteins of cyanobacteria. Cyanobacteria are among the simplest organisms that show circadian rhythm. As this model is coupled with equations of attractants and repellents adequately as in Figures 1 and 2 and as time constant moves appropriately, the system undergoes Hopf bifurcation to get a time periodic solution, and moreover, the periodic solution survives more robustly, as the number of sites is larger. In a consequence, we elucidate a piece of significant meaning of existence of a lot of sites in the receptor protein. In fact, in the case of circadian rhythm of cyanobacteria [3-4], a receptor protein monomer has two sites and it usually composes a hexamer, so that there are 12 sites per a hexamer of recepter protein. It seems that there is slightly many modification sites, but this contributes a stable oscillation daily. In our study, we ensure this fact by use of both deteministic and stochastic ways of simulations here. These two ways are not conflict with each other, but rather, these work to complement to each other. In fact, generally speaking, there may be fewer genes, proteins, and molecular than we can discuss about some qualitative and quantitative properties in a cell. In the case, it seems that we can hardly apply the model of differential equations to the interesting object. But in this paper, we ensure that the system preserves the hystrecally switching structure and robustness of time periodical behavior of solutions even in the corresponding model system of stochastic way. Moreover, we compute the average and variance of rotation number of the time-periodical solutions of the stochastic model to verify the advantage of a lot of site numbers.
Structure of a binary digit of memory in a cell
It is important how a binary digit of memory is realized in a cell, because a strange element must be steady and robust. In this section we propose a simple structure where the binary digit is constructed cleverly, and make an analysis of it. We are especially interested in correlation between the total site number and the steadiness of the binary digit. Moreover, we examine the robustness by changing several parameters in the model system.
Model equations
The basic assumptions are the following:
The receptor protein converges very rapidly to equilibrium between two configulations (S and T ).
S stands for a state which has accepted attractants and receives covalent modifiers one by one in a definite order. T stands for the opposite.
The equilibrium shifts towards the S form as the number of covalent modifiers is increasing. The total sites of the receptor protein is n. The total quantity of the receptor protein denotes Ctotal, and
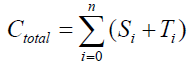 {1}
{1}
We illustrate our model in the following:
The total quantity of the attractant protein is denoted Atotal, and A represents a density of attractants and moreover, a part of the attractants is trapping in T'i . It is therefore satisfies that
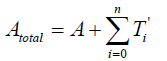 {2}
{2}
The intermediate state (T'i) satisfies
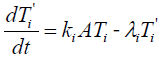 {3}
{3}
As it is assumed that the equilibrium state is realized very rapidly,
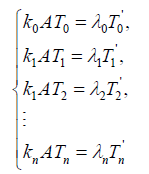 {4}
{4}
When we solve {2} and {4} about A , we have
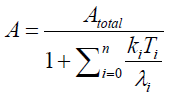 {5}
{5}
As a result, the model equation is the following:
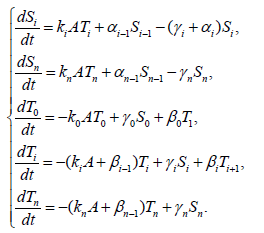 {6}
{6}
Here, i=1,2,3,…,n, and αi, βi, ki, λi, γi are positive constants. It is easy to understand that the quantity of the Ctotal is preserved. In fact, clearly we understand that 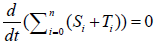 by summing up all the equations of the system of equations {6}.
by summing up all the equations of the system of equations {6}.
Mathematically rigorous analysis for 1-site model (n = 1)
If n=1, λ0=λ1=k0=k1=α0 =β0=1.0, and γ1=qγ0, then the system is {7}
where the constants satisfy
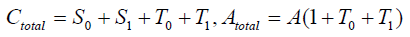
and where q>0 is the switching real parameter between two states. We can analyse it mathematically rigorous manner to get a theorem. The following theorem means that, if q is a moderate value, then the stationary problem of the system has a unique solution, but if q is a extreme big or small value, then the system has a hysteresis bifurcation structure in the stationary problem in the typical case.
Theorem 2.1: If 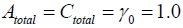 , then there are two real numbers
, then there are two real numbers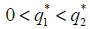 such that, if
such that, if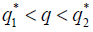 then the stationary problem of the system {7} has a unique solution, but either
then the stationary problem of the system {7} has a unique solution, but either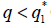 or
or 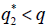 , then it has three stationary solutions.
, then it has three stationary solutions.
Proof: We use a linear transformation:
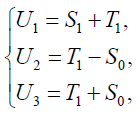 {8}
{8}
and get the transformed stationary problem:
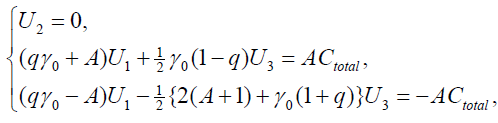 {9}
{9}
And
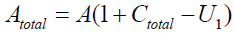
Therefore, we get the following, as U1’s equation:
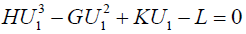
where the positive parameters are defined by
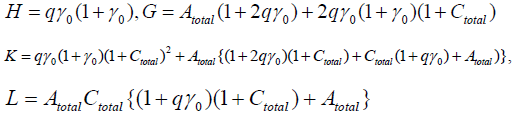
X and Y are different solutions of the above U1’s equation, and we see
H(X2+XY+Y2)–G(X+Y)+K=0.
Therefore the existence of X and Y are dependent upon the parameters’ value. Moreover, we can decide the number of the stationary solutions more precisely, if Atotal , Ctotal ,γ0 are adequately given.
Now we use the conditon: Atotal = Atotal = γ0 = 1.0, then
H=2q,G=10q+1,K=13q+4,L=2q+3.
We define the function y=f(x) by
f(x) =Hx3–Gx2+Kx–L,
and we can investigate to decide the positions of the roots of the equation f(x)=0 by use of primitive method (for instance, the positions of the extremal points are made determined, and the sign of the extremal value are also determined, and so forth), although the way is slightly long and complicated, but with simple idea. Then we obtain conclusion of the theorem.
Remark: Here we have shown the theorem in very special parameters, but in a slightly wider parameters’ area, the same kind of theorem holds actually. That fact can be ensured directly, although it is the same essentially as the above. Moreover, as the system of equations has a kind of covariance under some change of variables, it can be verified by this covariance, too.
Analysis
In previous subsection, we have gotten the rigorous theorem where we can see the system possessing hysteresis bifurcation structure in 1 site case. In multiple covalent modification sites case, we do not have the similar rigorous theorem, but numerical simulations reveal such a structure even in multiple site cases. Moreover, we see the width of hysteresis area be wider and wider, as the site number is bigger and bigger. This nature is very much related to memory reinforcement. For this purpose, we prepare some notations in the following:
Degree of covalent modification, P, is defined by
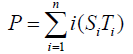 {10}
{10}
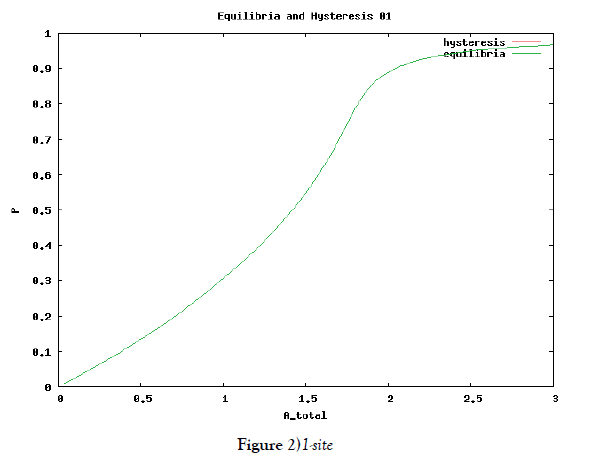
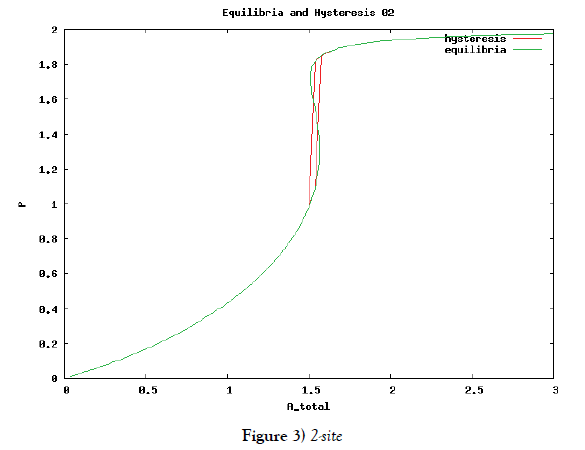
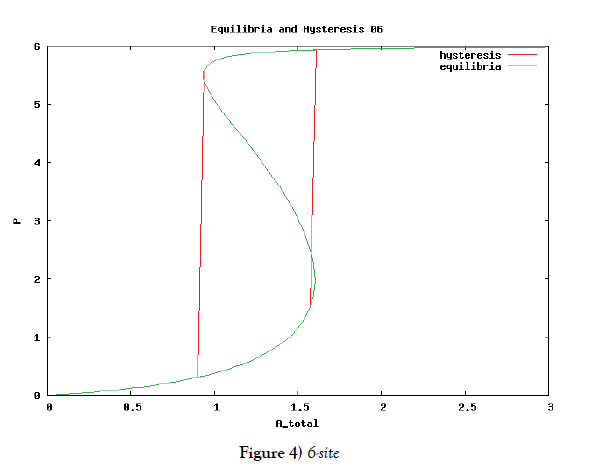
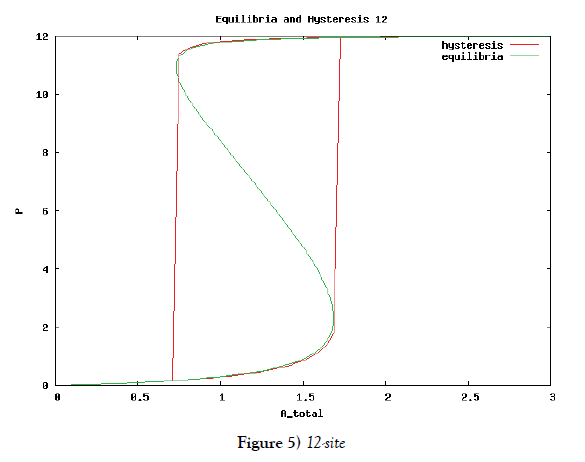
which means how many covalent modifiers the receptor protein totally possesses. How does P varies as the total attractants change? We investigate P’s behavior according to change of Atotal in {5}. Initial conditions of {6} are T0 =1.0 , Ti = 0.0, and Sj = 0.0 (i=1,2,3,…, and j=0,1,2,…,n) at first. We increase the value of Atotal from 0.01 to 10.0 step by step as a width of step is 0.01, and we plot the value of P after enough time goes by. Then an each initial state is successively made the final state just in the previous simulation. Inversely, we decrease the value of Atotal from 10.0 to 0.01 in the opposite manner, and plot it in the same figure. We repeat the same kind of numerical experiment in each possibly modifying site number. Moreover, we exactly solve the stationary problem of {6} in another way, and we make an infinitesimal stability analysis for each stationary solution. See Figures 2-5, and we see a bistable region existing and hysteresis occuring when the site number is bigger than two. In the figures, curves outside bistable region stand for stable branches of stationary solution, and a curve inside bistable region stands for unstable branch. The stable branches overlap completely with the final states in solving the time evolution equation, but the unstable branch goes inversely up (or down) the interior of in the bistable region, although at the end points the final states are jumping up (or down) to the nearest stable states in the same parameters. These are not overlapped with each other at all.
Circadian rhythm of cyanobacteria
In this section we consider the mathematical model of circadian rhythm of cyanobacteria by use of the model of a binary digit of strage element constructed and analized in the previous section. Before presenting our model, we briefly explain the circadian rhythm of cyanobacteria and the recent development.
The circadian rhythm of cyanobacteria is discovered in 1986 by Prof. s Kondo’s and Iwasaki’s [4-7] research group in Nagoya University. It is the most primitive life of organism obtaining circadian rhythm known so far. The clock genes (kaiA, kaiB, kaiC) and proteins (KaiA, KaiB, KaiC) have been already determined in [5]. Transcription–Translation roop had been considered as the core negative feedback roop of the circadian rhythm, but recently phosphorylation–dephosphorylation cycle of the clock protein, KaiC, continues to oscillate with 24 hours period in the constantly dark condition in [3], when all the transcription stop, although. Nowaday, at least in the case of cyanobacteria, the core cycle is thought of as this phosphorylation–dephosphorylation feedback roop composed of the clock proteins, KaiA, KaiB, and KaiC. Here KaiC is a receptor protein, and KaiA and KaiB are enzymes and work as attractants and as repellents, respectively. The possibly modifying number n is regarded as phosphorylation site of KaiC. Usually KaiC constructs hexamer and it has twelve phosphorylation sites. But according to T. Nishiwaki et al. [6], there are approximately 7.44 sites utilized in the average, when the phosphorylation of KaiC’s hexamer is maximum. In this section we let n moving from 2 to 12 to compare the qualitation properties.
Model equations
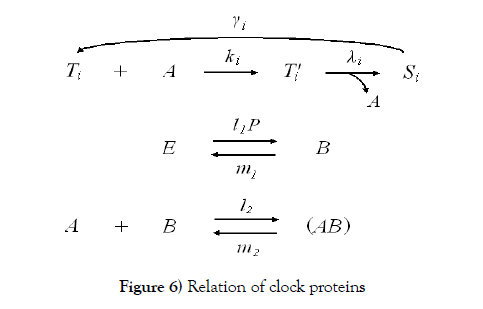
The clock protein KaiC is the receptor protein of phosphoric acids, and as it conbined with KaiA (which is another clock protein), it is likely to promote phosphorylation. The other clock protein KaiB is known as a repellent, which operates the complex KaiA–KaiC to let the receptor protein be likely to be dephosphorylation. The correlation is illustrated in Figure 6. As we consider that the total quantities of the three proteins must be preserved, respectively, by writing these as Atotal , Btotal , and Ctotal then we see
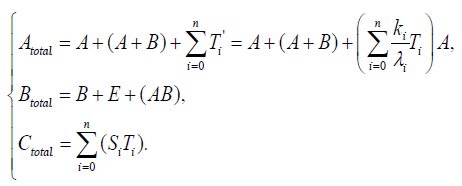 {11}
{11}
According to Figure 6, we present our model equations of A, (AB), and B, respectively.
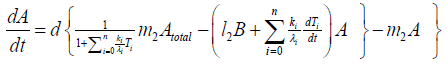 {12}
{12}
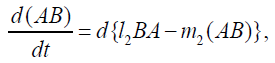 {13}
{13}
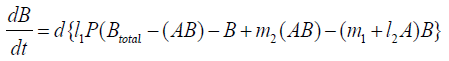 {14}
{14}
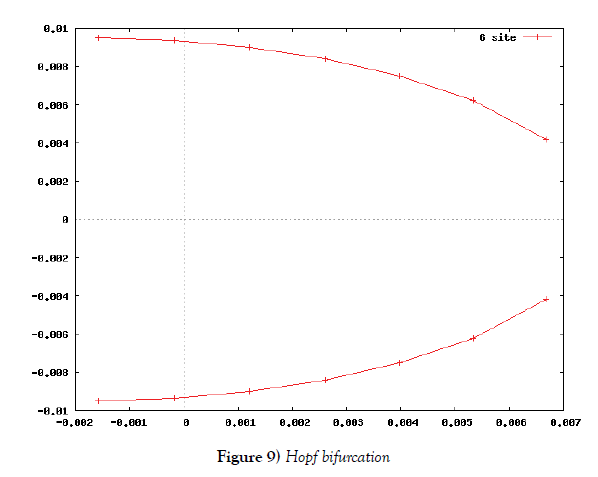
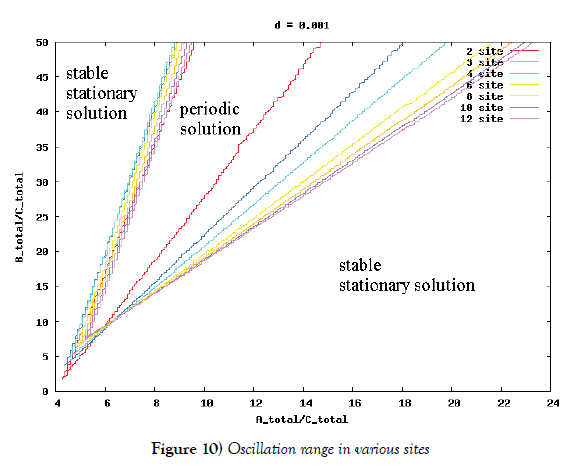
λi, ki (i=0,1,2,…,n), lj, mj (j=1,2), d are positive constents. We remark that {6}, {10}, {11}, {12}, {13}, and {14} are a consistent system of equations, although it seems to be surplus, apparently. In fact, we can derive the conservation law of Atotal in {11} by use of {12} and {13} easily. We remark that the right hand side of {12} has the terms dependent upon Ti or  , which come from the implicit change of A because of shift of chemical equilibrium according to A' s and B' s varying explictly. These terms need for conservation law of Atotal of [8-10]. We also list figures which means that Figures 7-9 shows bifurcation diagram of hysteresis loop and that Figure 10 shows how wider the hysteresis loop area grows, as the site number becomes larger, respectively.
, which come from the implicit change of A because of shift of chemical equilibrium according to A' s and B' s varying explictly. These terms need for conservation law of Atotal of [8-10]. We also list figures which means that Figures 7-9 shows bifurcation diagram of hysteresis loop and that Figure 10 shows how wider the hysteresis loop area grows, as the site number becomes larger, respectively.
Analysis
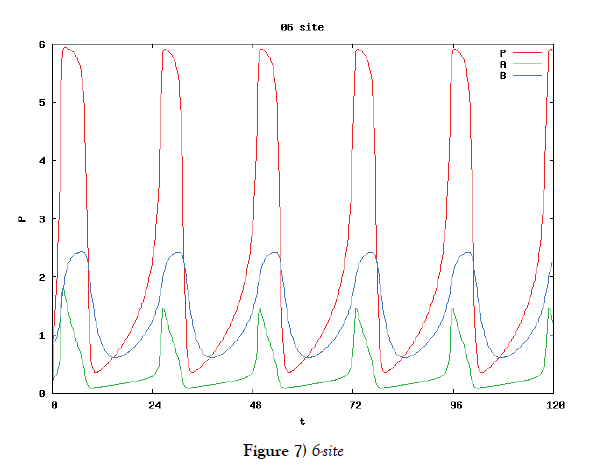
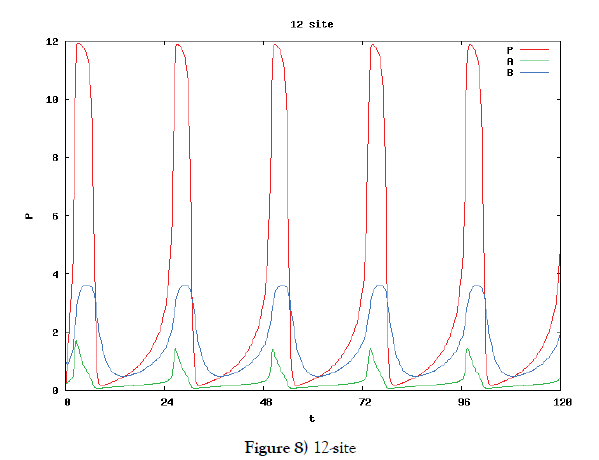
In this subsection we solve the system {6}, {10}, {11}, {12}, {13}, and {14}, numerically. First of all we ensure that it has a time periodic solution shown in Figures 7 and 8. These are generated by the corresponding hysteresis roop to bifurcations of hysteresis type of Figures 4 and 5.
Poisson process simulation
In this section we investigate the same system by use of stochastic process. In fact, this is important and useful, as each event of the chemical reactions in the system should be regarded as one following Poisson process.
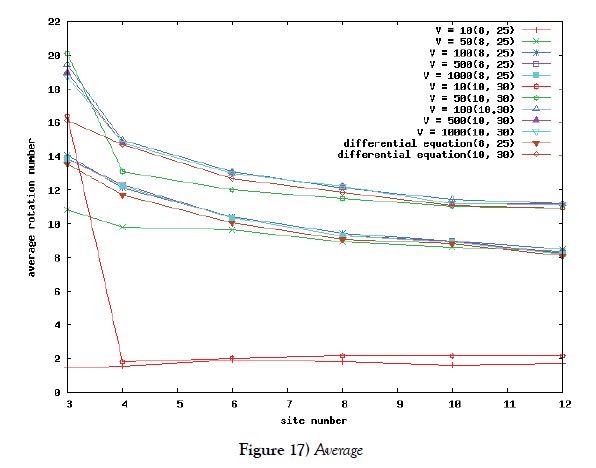
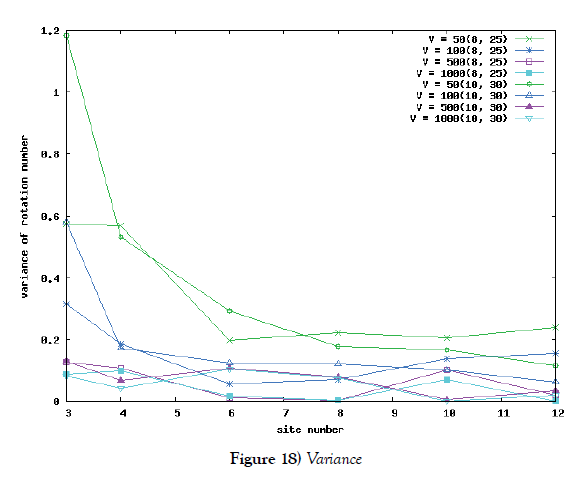
But in the case of a lot of site-numbers, it seems that shakes are relatively small. To ensure the site-number’s effect, we calculate the rotation number in the phase space of the system. The rotation number is defined as how many times the corresponding orbit rotates around the proper center point in the phase space. We first compare the average value of rotation number of Poisson process system with the rotation number of the system of differential equations. We moreover compute the variance of the value. By use of these value, we see a kind of stability of periodic solution of the system for this kind of shakes.
Discussion & Conclusion
We have proposed a standard structure of a binary digit of memory with multiple covalent modifications in a cell. This is composed of a receptor protein, attractants, repellents and covalent modifiers illustrated in Figure 1. As it is, the receptor protein operated by attractants becomes a state (say S ) which is likely to combine with a covalent modifier, and the one operated by repellents becomes a state (say T ) which is likely to release it. The receptor protein obtains n possibly modifying sites for covalent modifiers. S –T equilibrium is achieved very rapidly, and the equilibrium moves to S side more if the receptor protein has covalent modifiers more.
In § 2, we investigate the structure of a binary digit of strage element derived from our system of equations. If the possibly modifying site is exactly one, then the system does not have hysterical structure of stable stationary solution nor have digitally switching function. On the other hand, if the possibly modifying site is more than or equal to two, then it obtains both the structure and the function. We especially ensure that, if the site number is larger and larger, then both the structure and the function is more and more robust. We see this by the fact that, if the site number is more and more, then width of hysteresis is bigger and bigger. Furthermore, we investigate it by changing some parameters parameters of the system to get the relation between the site number and the robustness.
In § 3, we apply it to the circadian rhythm of cyanobacteria. The system of equations is derived from the known functions of KaiA and KaiB experimentally, as seen in {11}, {12}, {13}, and {14}. Especially, we note that {12} is more slightly complicated than expected, but this is from the considerlation of KaiA’s changing implicitly with shift of chemical equilibria in the equations {6) by the active KaiA’s varying explicitly. Interestingly, without using this exact formof KaiA’s equation, we can not see solutions of the system oscillating. This may sugest that the subtle adjustment of the equilibria shift to the KaiA’s changing has an important meaning for maintaining the oscillation solution.
Based on the biochemical reactions’ occuring in minutes order, we make time-rescaling to ensure that the 24-hour (1440-minutes) oscillation solutions exist if the site number is bigger than or equal to two. This fact is the first evidence of the contribution of many site numbers for stability of oscillation. We have also ensured that the oscillation solution comes from Hopf bifurcation by Figure 9.
Next, we investigate the oscillation range in ‘KaiA total’–‘KaiB total’plane to get Figure 10. According to this figure, if the site number is larger and larger, then the oscillation area is wider and wider. This is the second evidence for stability of oscillation. According to Kitayama et al. [8], the appropriate ratio of ‘KaiA total’, ‘KaiB total’, and ‘KaiC total’ is 3:9:1, which is computed in the number of molecules by use of both the moleculars weight and the mass ratio written in [8]. If the site number is bigger than six, then the half straight line of inclination three (which means the ratio 3:9 of ‘KaiA total’ and ‘KaiB total’) is include completely in the oscillation area, and vice versa. This also means the advantage of lots of site number.
In Ishiura et al. [5], they have made several biochemical experiments by use of mutants of Kai proteins to investigate change of the period of the circadian rhythm [9]. In the experiments using KaiA1 or KaiA2 mutants, they have reported that the period is made longer (33 hours or 30 hours) because the phosphorylation rate is smaller than in the wild type case. Our numerical simulations tell that surely in the case of KaiB’s total mass changing, the period is changed less than in the case of KaiA’s total mass changing. Moreover, they have also made a lot of experiments by use of KaiC’s mutants to get the result that the period changes from 16 hours to 60 hours or, in other cases, they obtain that the oscillation does not preserved. We also see the period changing qualitatively as long as the oscillations are surviving by our simulations. If we regard using KaiC mutants as all the KaiA’s and KaiB’s time constants’ or their reaction rates’ changing, then we understand why the width of change of the period is it in their experiments at least qualitatively.
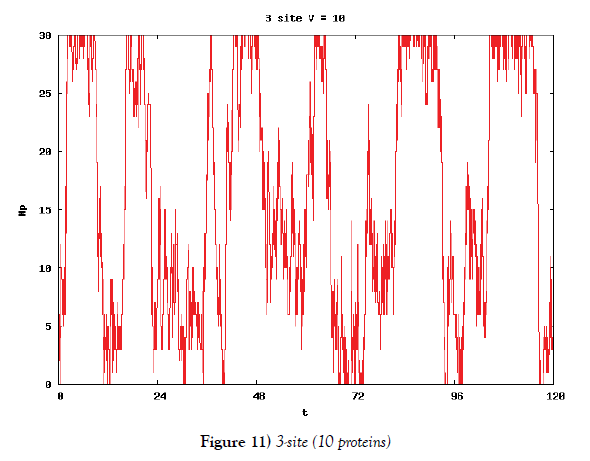
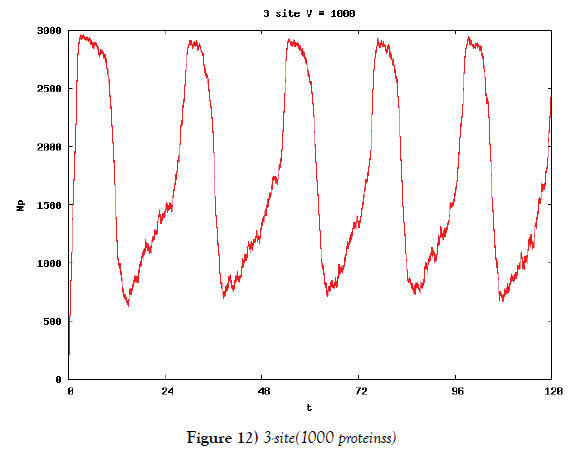
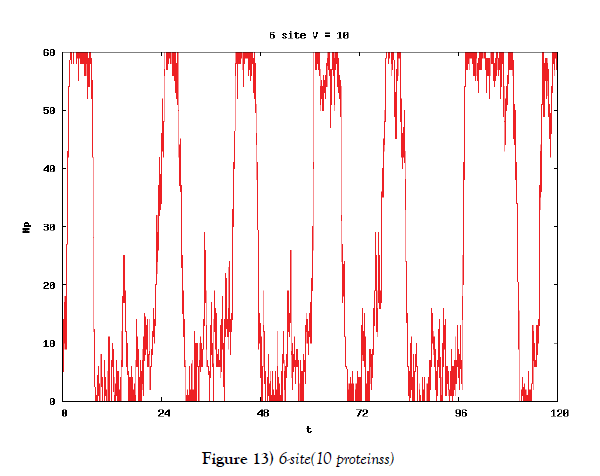
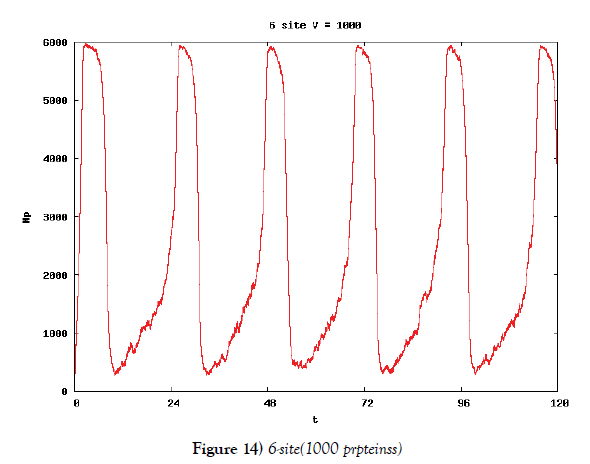
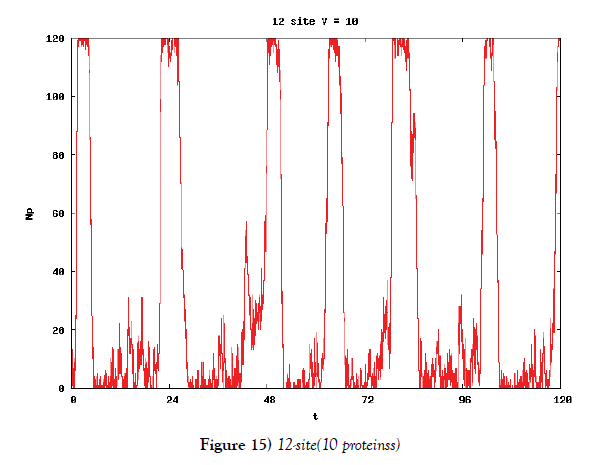
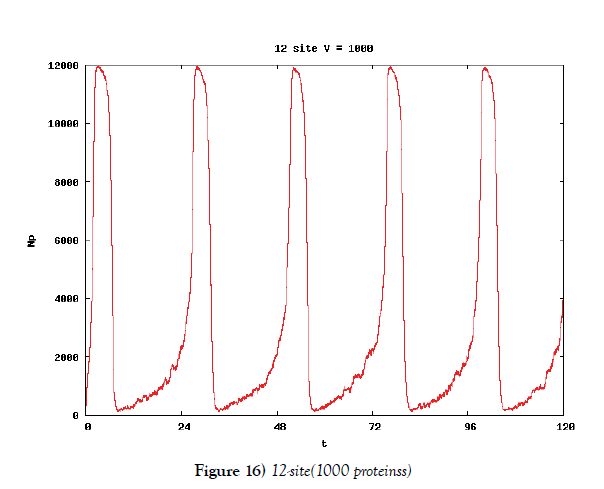
We make poisson process simulations to see how much the oscillations are robust in noisy situations, as real biochemical reactions occur stochastically. The result is that the oscillations are very robust, as seen from Figures 11- 16, in various site numbers and the number of molecules, V. Moreover, we make a calculation of change of the average values and the variance of the rotating number of the orbits in the phase spaces to get Figures 17 and 18. According to these figures, if V=10, then the average value is quite different from the rotation number of the orbit gotten by computations of differential equations. As seen in Figures 11, 13 and 15, these cases have too few numbers of molecules to preserve the similar oscillations to the original differential equations’ one, although, if the site number is twelve, then it seems that the difference is comparably little. From V=10 to V=1000, we calculate the variance of the rotating numbers, whose result is seen in Figure 18. If the site number is bigger than six, then the variance value is small independent from V ‘s values. This fact supports the advantage of a lot of possibly phosphorylating site number’s existence. Moreover, we can see the average used site number of a real KaiC–hexamer be 7.44 approximately in the paper, Nishiwaki et al. [6], when KaiC–hexamers are phosphorylated maximally. Our calculations also explain that comparably many sites are utilized actually in circadian rhythm of cyanobacteria, from the viewpoint of stability of 24-hours oscillations, very well. We furthurmore note that they reported there are more than 10000 molecules of Kai–proteins on a cell of cyanobacteria in Kitayama et al. [8]. This fact and our poisson process simulations tell us that it is significant to disscuss about the qulitative natures by use of properties of the solution-orbits of the system of ordinally differential equations. Recently, in Yoda et al. [10], they have reported that KaiC’s phosphorylations are shuffled to get averaged in a cell. This also supports our disscussions by the system of ordinary differential equations.
We eventually summarize our conclusions in the followings:
a) We propose a standard structure in which a binary digit of memory is constructed in a cell.
b) We give a rigorous proof of occurrence of hysteresis bifurcation of KaiA-KaiC stationary problem in 1-site case (n=1).
c) The robustness of the memory is reinforced more, if the possibly phosphorylating site numbers are larger.
d) If the site number is bigger than six, then the oscillations are comparably more stable even in fewer molecules.
e) Several biochemically experimental results about this circadian rhythm of cyanobacteria are comprehensible partially by our theory.
Acknowledgement
The author aprreciates Professor Tatsuo Shibata in Laboratory for Physical Biology RIKEN Quantitative Biology Center / RIKEN Center for Developmental Biology very much. He suggests that the Asakura-Honda improved model is very useful to make “A binary digit of memory” in a cell from the view point of Physical Biologist.
REFERENCES
- Asakura S, Honda H. Two-state Model for Bacterial Chemoreceptor Proteins. The Role of Multiple Methylation. J Mol Biol. 1984;176:349-367.
- Zon JS, Lubensky DK, Altena PRH, et al. An allosteric model of circadian KAiC phosphorylation, Proc Natl Acad Sci U S A. 2007;104:7420-7425.
- Tomita J, Nakajima M, Kondo T, et al. No transcription-translation feedback in circadian rhythm of KaiC phosphorylation. Science. 2005;307:251-254.
- Nakajima M, Imai K, Ito H, et al. Reconstitution of Circadian Oscillation of Cyanobacterial KaiC Phosphorylation in vitro. Science. 2015;308:414-415.
- Ishiura M, Kutsuna S, Aoki S, et al. Expression of a gene cluster kaiABC as a circadian feedback process in Cyanobacteria. Science. 1998;281:1519-1523.
- Nishiwaki T, Satomi Y, Nakajima M, et al. Role of KaiC phosphorylation in the circadian clock system of Synechococcus elongatus PCC 7942. Proc Natl Acad Sci U S A. 2004;101:13927-13932.
- Iwasaki H, Nishiwaki T, Kitayama Y, et al. KaiA-stimulated KaiC phosphorylation in circadian timing loops in cyanobacteria. Proc Natl Acad Sci U S A. 2002;99:15788-15793.
- Kitayama Y, Iwasaki H, Nishiwaki T, et al. KaiB functions as an attenuator of KaiC phosphorylation in the cyanobacterial circadian clock system, EMBO J. 2003;22:2127-2134.
- Mehra A, Hong CI, Shi M, et al. Circadian rhythmicity by autocatalysis. PLoS Comput Biol. 2006;2:e96.
- Yoda M, Eguchi K, Terada T, et al. Monomer-Shuffling and allosteric transition in KaiC circadian oscillation. Plos One. 2007;5:1-8.