The links of Pythagorean prime 137 to the fine structure constant, electrons’ Coulomb to gravitational force ratio, and the mass ratios of elementary particles

Received: 27-May-2023, Manuscript No. puljmap-23-6470; Editor assigned: 30-May-2023, Pre QC No. puljmap-23-6470; Accepted Date: Jun 23, 2023; Reviewed: 06-Jun-2023 QC No. puljmap-23-6470; Revised: 13-Jun-2023, Manuscript No. puljmap-23-6470; Published: 04-Jul-2023

Citation: Tang J, Tang B, Tang Q. The links of Pythagorean prime 137 to the fine structure constant, electrons��?��?��?���¢��?��??��?��?? Coulomb to gravitational force ratio, and the mass ratios of elementary particles. J Mod Appl Phys. 2023; 6(3):1-5.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

In this work, we present a model to unfold the century-old mysteries surrounding the fine structure constant and explain the physical origin of its value of ~1/137 due to gauge invariance, Einstein’s mass energy relation, and space time quantization. Using a generalized Dirac equation in a spacetime lattice, we obtain an estimate of an electron’s radius RRRR and also link the magic 137 beyond electromagnetism, to the ratio of the Coulomb and gravitational forces between a pair of electrons at 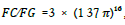, and t he m ass ratio s of an el ect ron to ot her particles such as a proton, Higgs boson, W/Z bosons, and quarks. With the proposed quantized space time, singularity divergence, and vacuum catastrophe problems in continuum quantum field theory can be avoided.

Key Words

Fine structure constant; Gauge invariance, Special relativity, Spacetime quantization

Introduction

One of the biggest mysteries in modern physics is the dimensionless fine structure constant, α = e² hc / , which happens to be about 1/137 [1]. This constant plays a crucial role in electromagnetism, and it strongly influences many physical processes in nature, including the evolution of stars and chemical reactions, yet no one knows why it takes such a value. The value of 137 has a substantial impact on life because should this value differ by more than 4%, stellar fusion would not produce carbon, and there will be no life on this planet [2, 3].

In this report, we present a theory to explain the origin of this value by linking the number theory [4, 5], regarding Pythagorean primes to Einstein’s mass-energy relation and the gauge theory in electromagnetism. In addressing this century-old mystery, we must postulate Spacetime Quantization (STQ), i.e., time and space are not divisible indefinitely, but possess a fundamental size. How STQ affects the foundations of physics would be like how Planck’s energy quantization influenced the quantum revolution. In this work, we will show how the fundamental unit of length and time leads to an electron’s quantized electric charge and mass.

We will also show how the gravitational constant is intricately connected to the fine structure constant for electromagnetism, implying the possible existence of a common root that unifies these two forces, and the potential unification of the quantum theory for gravity with other forces. In Dirac’s theory for electrons, the electric charge and mass are free parameters that must be determined experimentally. Currently, no accepted theories explain the origin of the electron’s charge and the value of the dimensionless fine structure constantα. In this work, we present an approach to link these values, along with the gravitational constant G, to more fundamental constants such as the speed of light and the Planck constant.

Theory

In this work, we present a model for the physical origin of the fine structure constant, based on spacetime quantization, gauge symmetry, and Einstein’s mass-energy relation. In quantized spacetime, space and time are not continuous and cannot be divided indefinitely. The concept of spacetime quantization is also assumed in the loop quantum gravity theory to treat the quantization of gravity [3, 4].

As will be shown later, by applying Einstein’s mass-energy relation to the quantized gauge function we could obtain the following equations:

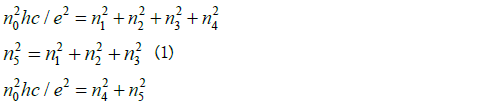
where hc/e² and n5 must be prime numbers, and n₀ = 1 for the primary set of integer solutions.

These constraints are necessary for the solution to represent the fundamental mode instead of higher harmonic modes. Before deriving Eq. (1) here we present the number theory of this magic prime 137 [5]. The constraints for the primary set of solutions for Eq. (1) lead naturally to hc/ e² =137

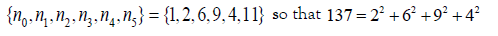
with 137 as a Pythagorean prime quintuple, and 137 = 4² +11² with 137 as a Pythagorean prime triple. In addition, one has 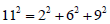with 11 as a prime and a Pythagorean quadruple. We have derived the ideal fine structure constant The small deviation from its experimental value 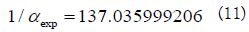of exp α is likely due to gauge symmetry breaking by weak interaction or the 654321`interaction of an electron with its own field [6]. Such a situation arises in the deviation of the gyromagnetic ratio from 2 for an ideal Dirac’s electron [7]. A slight increase in the effective fine structure constant observed at ~90 GeV is not surprising, because at such a regime hadron contribution due to interaction increases. The ideal 1/137 is like Dirac’s theory of a “bare” electron before QED renormalization.

We have obtained an empirical fit to the experimental value 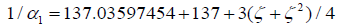by with in error for two expansion terms 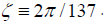of With five correction terms, one has 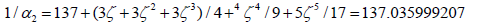shown an error of 10^-11

We now explain how to derive Eq. (1), based on the quantized gauge function in lattice spacetime. In continuous spacetime, the gauge transform of the wave function is invariant if λ(t, r) satisfies [8].

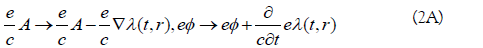
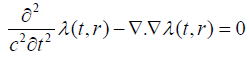and with discrete time and space, coordinates one has 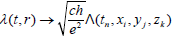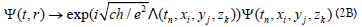Where,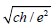and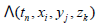are dimensionless, and the latter is related to the electric potential and vector potential. In quantized spacetime,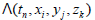 is no longer a continuous scalar function of time and space, so it needs to be replaced by operators, and the spacetime coordinates need to be expressed in terms of a fundamental length unit L and time unit T=L/c . Because the standing wave of the fundamental mode has a wavelength λ equals to twice the lattice length L, the fundamental unit for the wave vector and frequency is given by K = π/L and Ω = cπ/L, respectively.

Using an operator approach and a discrete Fourier transform, the gauge transformation 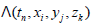which has a unit like momentum, can be replaced by a dimensionless operator Λ in 4D spacetime. One can define fundamental units for the wave vector π/L and frequency Ω = cπ/L. The gauge 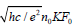function can be expressed in terms of four anti-commutative operators as

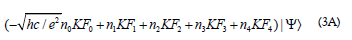
and

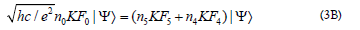
Where,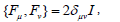

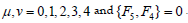One can use anti-commutative and orthonormal matrices α_k and β as in Dirac’s original paper [9] to represent, F_µ as

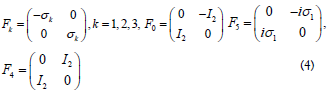
Where, F_k =α_k and F₄=β are idempotent, i.e.,

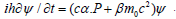By taking the square of these operators in Eq. (3A), one has

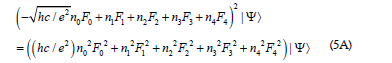
where all the cross terms vanish because of the anti-commutative relations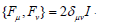

One has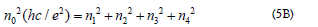

Finally, from Eqs. (3A) and (3B) we obtain the following equation involving a set of integers as

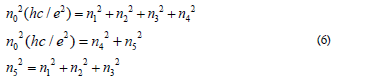
Where, hc/e² and n5 must be prime numbers for the solution to represent a fundamental mode, instead of higher harmonic modes For the fundamental mode’s solution, we obtained n₀=1= and hc/e² .

With the value of hc/e² determined, we found

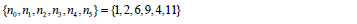
It indicates that 137 is not only a prime but also a Pythagorean prime quintuple 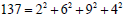with and a Pythagorean prime triple with 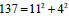.One also has 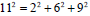,showing 11 a Pythagorean quadruple. From Eq. (6) one can notice that the index 11 is related to the magnitude of the total momentum vector, whereas the indices 2,6,9 are related to the momentum components along three spatial axes, and 4 is related to the internal energy due to the electromagnetic interaction. It is interesting to point out that 2×6×9 ×4=432 the product of the four integers for the Pythagorean prime quintuple of 137, equals approximately to 137π .

The lowest set of integers is called the primary set, and all other solutions correspond to higher harmonic modes with the index n0 greater than 1.

Using this primary set of integers, one can restore Eq. (6) to the original fundamental units K=π/L and frequency Ω=cπ/L to obtain

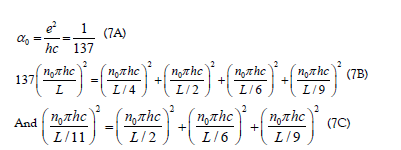
For the primary mode with n₀=1,Eq. (7B) is analogous to Einstein’s mass-energy-momentum relation

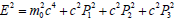
The last three terms 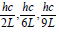are related to the particle’s kinetic energy along three spatial axes, and the term on the lefthand side of the equation represents the total mass energy. Eq. (7) contains different axial lengths in 4D spacetime and represents a hyper-cell structure. An electron can be regarded as in entangled coherent superposition of these degenerate eigenstates, and because of the couplings of the 4D coordinates to those anti-commutative operators, an electron possesses a ½ spin and can be regarded as a hyper-dimensional Mobius-type structure.

In Eq. (7) L is a scalable length factor, one might consider to assign it to the Planck length, but the corresponding energy of ~1018 GeV, a scale for grand unification, is unsuitable for the known elementary particles [9,10]. It is reasonable to assign its value to cover all elementary particles in the Standard Model [11]. Because of the ubiquitous presence of the scaling factor 137π in those empirical m formulae in Table 1, in addition to the constraints in Eq. (6), we also include a constraint for the search of the prime value for 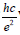with the ratio of the hyper-cell volume to the suitable prime be sufficiently close to an integer multiple of π . Because 432 137 ≈1.0037π ~π in our screening procedure for the prime value for 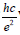we impose that it remain of the quotient to be <0.5%. After a screening algorithm to search all combinations of integer’s below10000,we have only found one primary solution with {n₁, n₂, n₃, n₄, n₅} = {2, 6, 9,4,11} that meets the constraints. The adjustable parameter K in Eq. (7) with K =π/L is related to L, the cube lattice constant, half wavelength of the fundamental standing wave. Before we discuss its link to the mass of elementary particles, we present in Table 1 a list of mass ratios between some elementary particles and that of an electron which is the lightest and most accurately determined value among fermions. We found links between 137 and the ratio between the Planck length and Re, and the mass ratios of the Higgs boson, W/Z bosons, top quark, and proton [12]. All these findings are summarized in Table 1. These simple relations provide hints about a possible role of 137 in all these particles.

TABLE 1. Links between 137 and the empirical mass ratios formulae of fundamental particles

Electron	Higgs boson
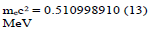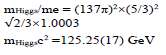W boson	Z boson
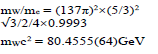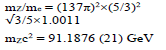Proton	Top quark
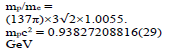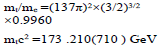Bottom quark	Charm quark

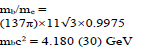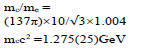To determine a suitable unit length, we use the electron as a reference. We obtain 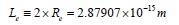with 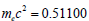[13], and the radius of an electron is

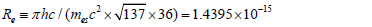
This factor 36 is the least common multiple of four axial length 4, 2, 6 and 9 for constructing a 4D perfect hyper-cube from hyper-cuboids. An electron can be regarded as in entangled coherence of three degenerate eigenstates, therefore, an electron has a symmetric shape. By equating the mass energy of an electron to the electrostatic energy of two point-like particle with the same electric charge as an electron, the distance is found to be 2.8179×10^-15 m, which is very close to the we obtained.

In comparison, the theoretical classical radius of an electron is 2.818×10^-15m, the experimental proton’s radius is about 0.842×10^-15, and the radius of a quark is about 10^-18m [14-16]. We have shown in Table 1, there are three tiers for the mass distribution of these elementary particles according to the power of their dependence on 137π.

Thus, it is reasonable for us to define the value of the minimum unit length 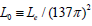so that the effective mass energy could cover the particles belonging to the 2nd tier, such as the Higgs boson, W/Z bosons and top quark. we do not assume that the size of an electron is the Planck length unit, but according to our lattice spacetime hypothesis we do assume all relevant physical sizes of elementary particles should be an integer multiple of the Planck length. The estimated radius of an electron is meant to represent the electron’s charge distribution.

According to Heisenberg uncertainty principle, the quantized energy of a particle in a box is inversely proportional to its size quantization. For an electron with a rest mass of only 0.511 Mev, an estimate size of about fm is reasonable, in comparison with a quark (with an estimate size of 10^-3 fm), which involves a much stronger force from the color charge than the electromagnetic force of an electric charge. Aside from the role that 137 plays in the electromagnetic force, the ratio between the Planck length and L₀, we have also discovered a link between 137 and the gravitational force. More specifically, by closely analyzing the ratio of the Coulomb to gravitational forces for a pair of electrons 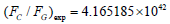we found a very simple formula 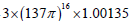with an error of only one part per thousand. Therefore, the presence of 137 in the simple dimensionless constant ratio 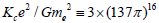strongly suggests a link of the fine structure constant in both the Coulomb force and the gravitation force. This formula hints that the prime 137 also plays an intricate role in gravity, and the power of 16 is likely related to sixteen pairwise operators in 4D spacetime according to the geometry algebra formalism. Our conjecture could provide a guideline for the theoretical development of quantum gravity.

We obtained an estimate 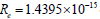of and found a relation for the ratio between the Planck length 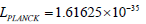and the electron’s radius R_e as

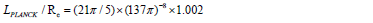
The comparisons between the experimental values and our empirical formulae that link these values to 137 are summarized in Table 2.

TABLE 2. The links between 137 and the Planck length and the ratio between Coulomb and gravitational forces for two electrons

Speed of light	Electron’s charge
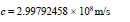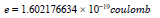Electron mass and radius Re	Planck constant
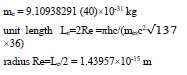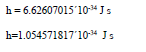Gravitational constant & Planck length	Coulomb constant
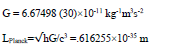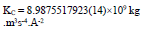Ratio between electrons’ Coulomb and gravitational forces	Ratio between Planck length and electron’s radius

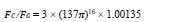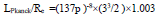Conclusion

In summary, we presented a model to explain the origin of the fine structure constant, and via Eq. (1) we can relate its inverse value to the number theory behind 137 as a Pythagorean prime of a triple, i.e., 137= 4² +11² , and also a Pythagorean prime of a quintuple, 137=4² +2² +6² +9² . We show that Eq. (1) is a natural consequence of spacetime quantization, gauge symmetry of the Lorentz group, and Einstein’s mass-energy relation. Due to spacetime quantization, the gauge function is shown to be quantized and can be expressed as a sum of 4×4 anti-commutative matrix operators αk and β, which are used by Dirac in his theory of electrons. The derivation of the prime 137 as an ideal value of the fine structure was constant compels us to postulate spacetime quantization. In this work, we unravel the mysterious role of prime 137 in the fine structure constant. We also found some very simple empirical formulae, such as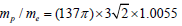

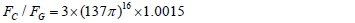
for the ratio of Coulomb and gravitation forces between two electrons. In addition, we also obtained a formula

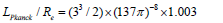
for the ratio between the Planck length and the electron’s radius. All these surprisingly simple relationships seem to imply that magic 137 plays an important role not only in electromagnetism but also has an intricate link to the other fundamental forces in nature. The hypothesis of the quantized spacetime is essential in our model, otherwise, this 137 value could not have arisen. We have found that with a quantized spacetime lattice the energy is quantized as an integer multiple of hπ/L, which is the lowest quantized energy with one quantum, and the vacuum corresponds to a state with no quanta that has no energy. This leads to the so-called vacuum catastrophe for the universe, where the predicted total energy for each kind of quantized field becomes a value about 120 orders of magnitude greater than the experimental value. The core hypothesis in our model that links 137 to the fine structure constant is the quantized spacetime. Also shared by loop quantum gravity community. It could alleviate some problems such as the self-energy divergence of an electron as a point-like object and the vacuum catastrophe problem in the quantum field theory of a continuum spacetime.

We have provided possible links between 137 to the masses of the quarks, proton, W and Z bosons, Higgs boson, the Planck length, and the Coulomb-to-gravitational force ratio, as shown in Tables 1 and 2, and these simple formulae appear to imply deep relationships among all four forces in nature. In this work, we present a model to explain the origin of the mysterious fine structure constant and shed light on the links between 137 and other types of forces.

The prescribed formulae in this work could potentially point a viable path toward the development of quantum gravity and grand unification theories. The perturbation refinement of the fine structure is constant due to symmetry breaking of the Lorentz group or interactions of an electron with its own field awaits further studies. Further theoretical developments are needed to quantitatively explain the origins behind the simple formulae that we have found and described in this report.

References

1. Kragh H. Magic number: A partial history of the fine-structure constant. Arch. Hist. Exact Sci. 2003; 57(5):395-431.

   [Googlescholar] [Crossref]

2. Sherbon MA. Fine-structure constant from Sommerfeld to Feynman. J. Adv. Phys. 2019; 16(1):335-43.

   [Googlescholar]

3. Ashtekar A, Bianchi E. A short review of loop quantum gravity. Reports on Progress in Physics. 2021; 84(4):042001.

   [Googlescholar] [Crossref]

4. Takloo Bighash, R. A Pythagorean Introduction to Number Theory. Springer Press. 2018

   [Googlescholar]

5. Morel L, Yao Z, Clade P, et al. Determination of the fine-structure constant with an accuracy of 81 parts per trillion. Nature. 2020; 588(7836):61-5.

   [Googlescholar] [Crossref]

6. Brodsky SJ, Drell SD. Anomalous magnetic moment and limits on fermion substructure. Physical Review D. 1980; 22(9):2236.

   [Googlescholar] [Crossref]

7. O’Raifeartaigh L, Straumann N. Gauge theory: Historical origins and some modern developments. Reviews of Modern Physics. 2000; 72(1):1.

   [Googlescholar] [Crossref]

8. Dirac PA. The quantum theory of the electron. Proceedings of the Royal Society A. 1928; 117(778):610-24.

   [Googlescholar] [Crossref]

9. De Boer W. Grand unified theories and supersymmetry in particle physics and cosmology. Progress in Particle and Nuclear Physics. 1994; 33:201-301.

   [Googlescholar] [Crossref]

10. Schwartz MD. Quantum field theory and the standard model. Cambridge university press; 2014.

    [Googlescholar]

11. Magic number: A partial history of the fine-structure constant
12. Mohr PJ, Newell DB, Taylor BN. CODATA recommended values of the fundamental physical constants. 2016; 45(4):043102.

    [Googlescholar] [Crossref]

13. Pythagorean prime. Wikipedia. 2023 [Googlescholar]
14. Gaarder Haug E. The gravitational constant and the Planck units. A simplification of the quantum realm. Physics Essays. 2016; 29(4):558-61.

    [Googlescholar] [Crossref]

15. Golden angle. Wikipedia. 2023
16. Quigg C. Gauge theories of the strong, weak, and electromagnetic interactions. Princeton University Press; 2013.

    [Googlescholar].