Modeling virus as elastic sphere in newtonian fluid based on 3d Navier-Stokes equations

Received: 26-Nov-2017 Accepted Date: Feb 05, 2018; Published: 15-Feb-2018

Citation: Christianto V, Smarandache F. Modeling virus as elastic sphere in newtonian fluid based on 3d Navier-Stokes equations. J Nanosci Nanomed.. March-2018;2(1):1-2.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

Although virus is widely known to significantly affect many biological form of life, its physical model is quite rare. In this regard, experiments on the acoustic vibrations of elastic nanostructures in fluid media have been used to study the mechanical properties of materials, as well as for mechanical and biological sensing. The medium surrounding the nanostructure is typically modeled as a Newtonian fluid. In this paper, we present a mathematical model of virus as an elastic sphere in a Newtonian fluid, i.e. via 3D Navier-Stokes equations. We also obtain a numerical solution by the help of Mathematica 11.

Keywords

Newtonian fluid; virus model; nonlinear physics; 3D Navier-Stokes equations; computational physics

Introduction

Although virus is widely known to significantly affect many biological form of life, its physical model is quite rare. In a paper, L.H. Ford wrote:

“Two simple models for the particle are treated, a liquid drop model and an elastic sphere model. Some estimates for the lowest vibrational frequency are given for each model. It is concluded that this frequency is likely to be of the order of a few GHz for particles with a radius of the order of 50nm” [1].

Such an investigation on acoustic vibration of virus particles may resonate with other reports by Prof. Luc Montagnier [2,3] and also our own hypothesis [4,5] on wave character of biological entities such as DNA, virus, water, etc.

In this regard, there are studies on the mechanical properties of (biology) materials based on experiments on the acoustic vibrations of elastic nanostructures in fluid media, where the medium surrounding the nanostructure is typically modeled as a Newtonian fluid.

In this paper we will also discuss a Newtonian fluid, i.e. 3D Navier-Stokes equations.

It is our hope that the new proposed method can be verified with experiments.

A Model of Linearized Navier-Stokes Equations

In 2015, Vahe Galstyan, On Shun Pak and Howard A. Stone published a paper where they discuss breathing mode of an elastic sphere in Newtonian and complex fluids [6]. They consider the radial vibration of an elastic sphere in a compressible viscous fluid, where the displacement field of the elastic fluid medium is governed by the Navier equation in elasticity. This spherically symmetric motion is also called the breathing mode.

They use a linearized version of Navier-Stokes equations, as follows: [6]

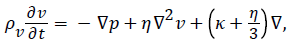(1)

where ρv is the density of the fluid, η is the shear viscosity, κ is the bulk viscosity, and p is the thermodynamic pressure.

There are other authors who work on linearized NS problem; here we mention a few of them: Foias and Saut [7], Thomann and Guenther [8], A. Leonard [9].

Numerical Solution of 3D Navier-Stokes Equations

In fluid mechanics, there is an essential deficiency of the analytical solutions of non-stationary 3D Navier–Stokes equations. Now, instead of using linearized NS equations as above, we will discuss a numerical solution of 3D Navier-Stokes equations based on Sergey Erhskov’s papers [10,11].

The Navier-Stokes system of equations for incompressible flow of Newtonian fluids can be written in the Cartesian coordinates as below (under the proper initial conditions): [10]

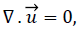(2)

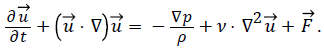(3)

Where u is the flow velocity, a vector field, ρ is the fluid density, p is the pressure, v is the kinematic viscosity, and F represents external force (per unit mass of volume) acting on the fluid. [10]

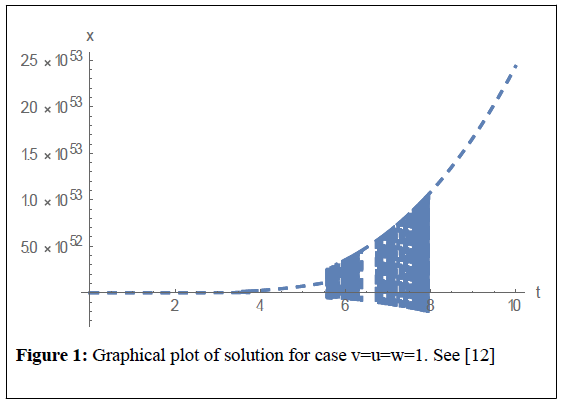
In ref. [10], Ershkov explores new ansatz of derivation of non-stationary solution for the Navier–Stokes equations in the case of incompressible flow, where his results can be written in general case as a mixed system of 2 coupled-Riccati ODEs (in regard to the time-parameter t). But instead of solving the problem analytically, we will try to find a numerical solution with the help of computer algebra package of Mathematica 11 (Figure 1).

Figure 1: Graphical plot of solution for case v=u=w=1. See [12]

The coupled Riccati ODEs read as follows: [10]

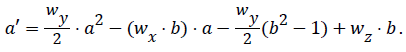(4)

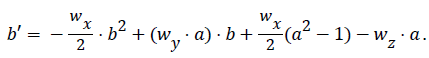(5)

First, equations (4) and (5) can be rewritten in the form as follows:

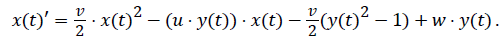(6)

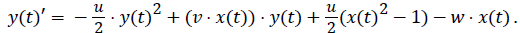(7)

Then we can put the above equations into Mathematica expression: [12]

v=1;

u=1;

w=1;

{xans6[t_],vans6[t_]}={x[t],y[t]}/.Flatten[NDSolve[{x'[t]==(v/2)*x[t]^2- (u*y[t])*x[t]-v/2)*(y[t]^2-1)+w*y[t], y'[t]==-(u/2)*y[t]^2+(v*x[t])*y[t] +(u/2)*(x[t]^2-1)-w*x[t], x[0]==1,y[0]==0}, {x[t],y[t]},{t,0,10}]]

graphx6 = Plot [xans6[t],{t,0,10}, Axes Label->{"t","x"}, Plot Style- >Dashing[{0.02,0.02}]];

Show [graphx6,graphx6]

The result is as shown below: [12]

Concluding Remarks

In this paper we review 3D Navier-stokes equations obtained by Ershkov, as a model of virus as an elastic sphere in Newtonian fluid, and we solve the equations numerically with the help of Mathematica 11.

It is our hope that the above numerical solution of 3D Navier-Stokes equations can be found useful in mathematical modeling of virus.

All in all, here we would like to emphasize that such an investigation on acoustic vibration of virus particles may resonate with other reports by Prof. Luc Montagnier and also our own hypothesis, on wave character of biological entities such as DNA, virus, water, etc. [2-4][13,14].

We are quite optimistic that this novel approach can lead to new kinds of nanomedicine of virus based on acoustic vibration in Newtonian fluid medium.

Acknowledgement

Special thanks to three anonymous reviewers for comments, and also to Sergey Ershkov from Lomonosov’s Moscow State University for reading our initial manuscript and suggesting improvement.

REFERENCES

1. Ford LH. An estimate of the Vibrational Frequencies of Spherical Virus Particles 2003.
2. Montagnier L, Aissa J, Giudice ED, et al. DNA waves and water 2010.
3. Montagnier L. DNA between physics and biology 2014.
4. Umniyati Y, Christianto V. A non-particle view of DNA and implications to cancer therapy 2016.
5. Christianto V, Umniyati Y. A few comments of Montagnier and Gariaev's works. DNA Decipher Journal 2016.
6. Galstyan V, Pak OS, Stone HA. A note on the breathing mode of an elastic sphere in Newtonian and complex fluids 2015.
7. Foias C, Saut JC. Linearization and normalization of Navier-Stokes equations with potential forces. Annales de l’I.H.P., section C, tome 4 no. 1 1987;1-47.
8. Thomann EA, Guenther RB. The Fundamental Solution of the Linearized Navier Stokes Equations for Spinning Bodies in Three Spatial Dimensions-Time Dependent Case.  Journal of Math. Fluid Mech.2006;8:77-98.
9. Leonard A. Approximate Solutions to the Linearized Navier-Stokes Equations for Incompressible Channel Flow 2016.
10. Ershkov SV. Non-stationary Riccati-type flows for incompressible 3D Navier–Stokes equations. Computers and Mathematics with Applications 2016;71:1392–1404.
11. Ershkov SV. A procedure for the construction of non-stationary Riccati-type flows for incompressible 3D Navier–Stokes Equations. Rend. Circ. Mat. Palermo 2016;65:73–85.
12. Christianto V, Ershkov SV. Solving Numerically a System of Coupled Riccati ODEs for Incompressible Non-Stationary 3D Navier-Stokes Equations 2017.
13. Shingareva I, Lizarraga-Celaya C. Solving Nonlinear Partial Differential Equations with Maple and Mathematica. Dordrecht : Springer 2011;371.
14. Tam PT. A Physicist’s guide to Mathematica. 2nd ed. Amsterdam: Academic Press - an imprint of Elsevier 2008;749.