Theoretical study of obliquely propagating whistler mode wave for ring distribution in the magnetosphere
2 Department of Physics, Amity Institute of Applied Sciences, Amity University, Uttar Pradesh, India, Email: JyotiKumari@amity.edu
Received: 19-Apr-2018 Accepted Date: May 04, 2018; Published: 11-May-2018
Citation: Varughese G, Kumari J, Pandey RS, et al. Theoretical study of obliquely propagating whistler mode wave for ring distribution in the magnetosphere. J Mod Appl Phys. 2018;2(1):13-17.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
Changes in plasma density and magnetic fields have a strong influence on the propagation of very low frequency waves in the Whistler mode. It is suggested that the earth’s magnetic field be called the ‘magnetosphere’ region. Van Allen and others observations show that this area reaches 5 to 10 Earth radii depending on the degree of magnetic interference. In the present paper, whistler mode waves in the magnetosphere of Earth have been investigated. For whistler mode waves, linear properties of ring distribution function are used to derive the dispersion relation. Method of characteristics by the kinetic approach has been used to investigate whistler waves. The present analysis shows that the growth rate of electromagnetic circularly polarized whistler mode wave has been found to be increasing with increasing temperature anisotropy and number density. It has been found that the growth rate decreases with an increase in the angle of propagation. As the electron energy shows significant effect on growth rate. The growth rate increases along with a significant shift in wave number with increasing temperature anisotropy, number density and energy density. The analytical model developed can also be applied to the other planetary magnetospheres for understanding various types of instabilities.
Keywords
Magnetosphere of Earth; Whistler mode waves; Ring distribution function
Introduction
In all planets with magnetic fields, the main energy driving sources for the magnetic layer process are planetary rotation and solar wind. On Earth, the main source of energy is solar wind. A magnetosphere is that area of space around a planet which is controlled by the planet’s magnetic field. Its shape is a direct result of being blasted by solar wind. The effect of solar wind is the compression of its sunward side up to 6 to 10 times the radius of the earth (RE=6400 Km). Due to this a supersonic shock wave is created known as Bow shock at which most of the solar wind particles are heated and slowed and detour in the magnetosheath around the Earth. The Earth’s magnetosphere is the strongest one of all the rocky planets among the solar system. Convective motion of charged molten iron far below the surface of Earth’s outer core is one of the reasons for the generation of its magnetosphere. The auroral magnetosphere of Earth is an active region for numerous activities of plasma waves. The plasma in auroral region is characterized by 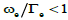 where
where 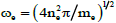 is the plasma frequency and
is the plasma frequency and 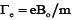 is the gyrofrequency. Large number of ground based observations and spacecrafts have shown that wave particle interactions are very important processes in the auroral region. The basic concepts of wave particle interaction have been reported by [1] in the collision-less plasma. Radio wave emissions in the ground level of auroral region have been observed by [2] in the frequency range of 150-700 kHz. Theoretical study done by [3] indicates that the whistler mode waves propagating parallel in the frequency range of 150-700 kHz are excited by the energetic electrons trapped in the auroral region with higher energies of keV due to the temperature anisotropy. Different sources of free energy existing in the earth’s magnetosphere give rise to instabilities, like uneven distribution of temperature, ambient magnetic field, energy density etc. Earth’s magnetic field can be viewed as a dipole with north and South Pole which are acting as a bar magnet. It is now possible to study the area above the ionosphere, where the Earth’s magnetic field has dominant control over the movement of gases and rapidly charged particles. It is known that the area extends to a distance of 10 Earth radii and is called the magnetic layer. Although only the most basic information about the behavior of the area is available at the moment, it makes sense to investigate the laws that dictate the movement of material there. One of the global wave modes observed in the space plasma is Whistler mode waves. Their observations in the magnetosphere, in the solar wind, in upstream of planetary bow shocks, in cometary foreshocks and in upstream of interplanetary shocks have been reported by [4-8]. Very low frequency whistle mode waves are omnipresent in the Earth’s magnetosphere, especially the plasma layer. It is well known that whistle can be confined to an enhanced or depleted field-aligned plasma density irregularity or duct region, in a process called as ducting. The observations made by spacecrafts have proven the presence of ducts in the plasma sphere near equator [9,10], which are correlated with a considerable whistler activity, mainly near the plasmapause [9]. These waves are righthand polarized electromagnetic waves. Whistler mode waves can propagate along the magnetic field, perpendicular to the magnetic field and obliquely to the magnetic field as a quasi- electrostatic mode near the resonance cone [11]. These waves provide a variety of emissions in the magnetoplasma [12] Energetic electrons triggered by external emissions can cause coherent whistler emissions [13]. It is assumed that whistler mode waves are driven unstable by temperature anisotropies of electrons in the magnetosphere [14]. Because of the strong interaction of whistler mode waves with energetic particles [14,15], it has been accepted that these waves play an important role in global radiation belt dynamics. Thus, whistler mode waves have been a topic of attention for over 40 years in magnetospheric physics. In 1966, scattering of electrons into the loss cone by incoherent whistler’s radiation was treated by Kennel, et al. [14]. Unan [16] considered pitch angle scattering by emissions of coherent whistlers. The effect of temperature anisotropy and pitch angle anisotropy on growth rate and emission frequency in case of hot energetic electrons has been studied. HuangL et al. [17] calculated the characteristics of incoherent whistler mode waves which are generated in the magnetosphere along L=5 geomagnetic field line. Measurements of plasma waves are mainly consisted of time-averaged spectral intensity data for the past 30 years. For electric field, time averaged spectral zero-to-peak amplitudes for whistler mode waves are ∼0.5 mV/m [18] and for magnetic field, it is ∼0.01-0.1 nT [19,20]. Large amplitude whistler mode waves were discovered in the radiation belts having amplitude >200mV/m using the STEREO spacecraft [21], and afterwards it was observed by spacecraft Wind [22] and THEMIS [23]. Electrons can gain energy by more than an MeV in less than a second by these waves [21] and consistency between this and test particle stimulation has been found by [24,25].
is the gyrofrequency. Large number of ground based observations and spacecrafts have shown that wave particle interactions are very important processes in the auroral region. The basic concepts of wave particle interaction have been reported by [1] in the collision-less plasma. Radio wave emissions in the ground level of auroral region have been observed by [2] in the frequency range of 150-700 kHz. Theoretical study done by [3] indicates that the whistler mode waves propagating parallel in the frequency range of 150-700 kHz are excited by the energetic electrons trapped in the auroral region with higher energies of keV due to the temperature anisotropy. Different sources of free energy existing in the earth’s magnetosphere give rise to instabilities, like uneven distribution of temperature, ambient magnetic field, energy density etc. Earth’s magnetic field can be viewed as a dipole with north and South Pole which are acting as a bar magnet. It is now possible to study the area above the ionosphere, where the Earth’s magnetic field has dominant control over the movement of gases and rapidly charged particles. It is known that the area extends to a distance of 10 Earth radii and is called the magnetic layer. Although only the most basic information about the behavior of the area is available at the moment, it makes sense to investigate the laws that dictate the movement of material there. One of the global wave modes observed in the space plasma is Whistler mode waves. Their observations in the magnetosphere, in the solar wind, in upstream of planetary bow shocks, in cometary foreshocks and in upstream of interplanetary shocks have been reported by [4-8]. Very low frequency whistle mode waves are omnipresent in the Earth’s magnetosphere, especially the plasma layer. It is well known that whistle can be confined to an enhanced or depleted field-aligned plasma density irregularity or duct region, in a process called as ducting. The observations made by spacecrafts have proven the presence of ducts in the plasma sphere near equator [9,10], which are correlated with a considerable whistler activity, mainly near the plasmapause [9]. These waves are righthand polarized electromagnetic waves. Whistler mode waves can propagate along the magnetic field, perpendicular to the magnetic field and obliquely to the magnetic field as a quasi- electrostatic mode near the resonance cone [11]. These waves provide a variety of emissions in the magnetoplasma [12] Energetic electrons triggered by external emissions can cause coherent whistler emissions [13]. It is assumed that whistler mode waves are driven unstable by temperature anisotropies of electrons in the magnetosphere [14]. Because of the strong interaction of whistler mode waves with energetic particles [14,15], it has been accepted that these waves play an important role in global radiation belt dynamics. Thus, whistler mode waves have been a topic of attention for over 40 years in magnetospheric physics. In 1966, scattering of electrons into the loss cone by incoherent whistler’s radiation was treated by Kennel, et al. [14]. Unan [16] considered pitch angle scattering by emissions of coherent whistlers. The effect of temperature anisotropy and pitch angle anisotropy on growth rate and emission frequency in case of hot energetic electrons has been studied. HuangL et al. [17] calculated the characteristics of incoherent whistler mode waves which are generated in the magnetosphere along L=5 geomagnetic field line. Measurements of plasma waves are mainly consisted of time-averaged spectral intensity data for the past 30 years. For electric field, time averaged spectral zero-to-peak amplitudes for whistler mode waves are ∼0.5 mV/m [18] and for magnetic field, it is ∼0.01-0.1 nT [19,20]. Large amplitude whistler mode waves were discovered in the radiation belts having amplitude >200mV/m using the STEREO spacecraft [21], and afterwards it was observed by spacecraft Wind [22] and THEMIS [23]. Electrons can gain energy by more than an MeV in less than a second by these waves [21] and consistency between this and test particle stimulation has been found by [24,25].
The unstable ring distribution function provides an important source of free energy, so it can excite plasma waves [8,26,27]. In weakly collisional plasma, for different types of instabilities, the ring distribution function acts as a source of free energy [28,29]. Effective temperature anisotropies and differential scattering are found to be the reason of this [30-32]. Electromagnetic whistler waves, below the electron cyclotron frequency, are excited by temperature anisotropy in hot ring distribution [33]. We have studied whistler mode waves using ring distribution function. Therefore, in the present work, we investigate linear growth of whistler mode waves in the Earth’s magnetosphere. Since Earth’s magnetospheric plasma consists of a huge number of particles and waves interacting with each other [34], it is suitable to present a macroscopic description of plasma phenomena by using a statistical approach. [35] were first to develop Kinetic approach. Thus in present work analytical approach has been applied to derive the dispersion relation for ring distribution. Using dimensionless integrals, dependence of wave growth rate has been determined. We have obtained analytical solutions in terms of Bessel functions in the following section.
Dispersion Relation
Spatially homogeneous anisotropic, collisionless plasma subjected to external magnetic field has been considered to get dispersion relation. Linearized Vlasov-Maxwell equations are obtained after neglecting higher order terms and separating the equilibrium and non-equilibrium parts. Following the technique of [36,37], Vlasov equations are given as below:
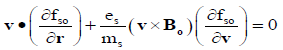 (1)
(1)
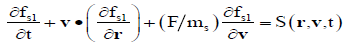 (2)
(2)
Where force is given as 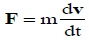
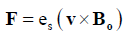 (3)
(3)
The particle trajectories are obtained by solving an equation of motion defined in equation (3) and S(r, v, t) is defined as:
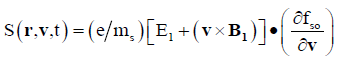 (4)
(4)
Where S denotes species and E1, B1 and fs1 are perturbed quantities and are assumed to have harmonic dependence in E1, B1 and fs1=exp i(k.r − ωt).
The method of characteristic solution is used to determine the perturbed distribution function, fs1, which is obtained from Eq. (2) by
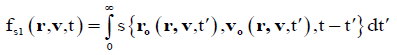 (5)
(5)
The phase space coordinate system has been transformed from (r,v,t) to 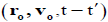 . The particle trajectories which are obtained by solving eq. (3) for the given external field and wave propagation,
. The particle trajectories which are obtained by solving eq. (3) for the given external field and wave propagation, 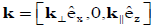 are:
are:
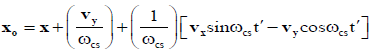 (6a)
(6a)
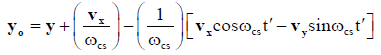 (6b)
(6b)
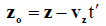 (6c)
(6c)
And the velocities are
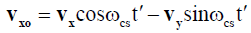 (7a)
(7a)
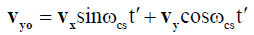 (7b)
(7b)
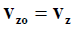 (7c)
(7c)
Where 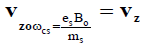 cyclotron frequency of species After some algebraic simplifications and integration, the perturbed distribution function is given as:
cyclotron frequency of species After some algebraic simplifications and integration, the perturbed distribution function is given as:
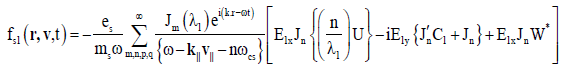
Where 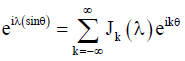 is the Bessel identity. It has been used as an argument of the following functions:
is the Bessel identity. It has been used as an argument of the following functions:
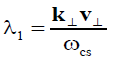 (8a)
(8a)
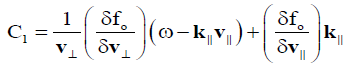 (8b)
(8b)
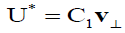 (8c)
(8c)
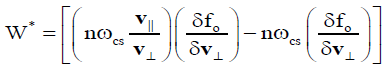 (8d)
(8d)
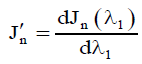 (8e)
(8e)
The conductivity tensor is written as:
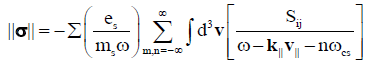 (9)
(9)
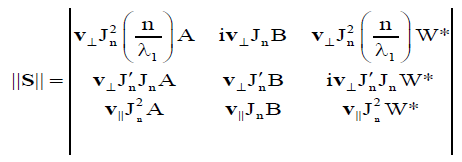 (10)
(10)
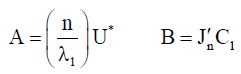 (11)
(11)
From J = ||σ||.E1 and two Maxwell’s curl equations for the perturbed quantities, the wave equations can be written as:
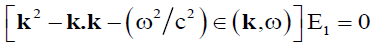 (12)
(12)
Where ||∈(k,ω)|| =1− (4π iω)||σ(k,ω)|| =dielectric tensor (13)
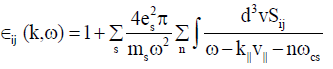 (14)
(14)
Expression for Growth Rate
For whistler mode propagation and instability with 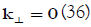 , the branch of general dispersion relation [14] reduces to:
, the branch of general dispersion relation [14] reduces to:
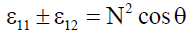 (15)
(15)
Where N2 = (k2c2 )/ω2 is refractive index. Therefore dispersion relation for n=1 may be written as:
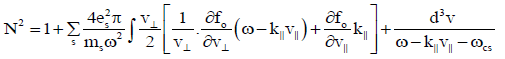 (16)
(16)
The distribution function for trapped electron is taken as Maxwellian Ring velocity distribution [38,39]:
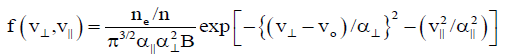 (17)
(17)
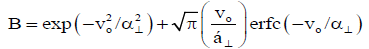 (18)
(18)
In equation (17), ne/n is the ratio of trapped energetic electrons to total electron density (ne/n=no). Equation (18) gives the expression for complimentary error function. The v|| and v⊥ are parallel and perpendicular velocities with respect to magnetic field. vo is the drift speed.
Following are the expressions for associated parallel and perpendicular electron thermal velocities:
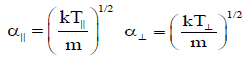
Using equation (17) and substituting 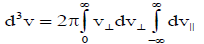 in equation (16) we solve the integrals to get dispersion relation as:
in equation (16) we solve the integrals to get dispersion relation as:
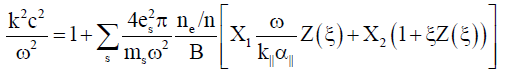 (19)
(19)
Where,
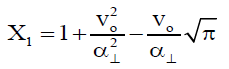
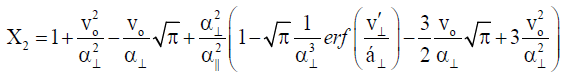
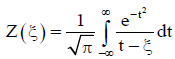 is the plasma dispersion function with
is the plasma dispersion function with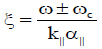
Applying condition 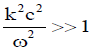 for whistler waves
for whistler waves
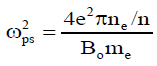
ω = ω + iγ
The equation (19) reduces to
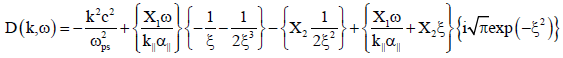 (20)
(20)
Introducing the dimensionless parameters as 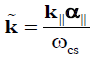
The growth rate in terms of the dimensionless parameters 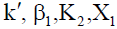 and
and 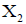 is obtained as
is obtained as
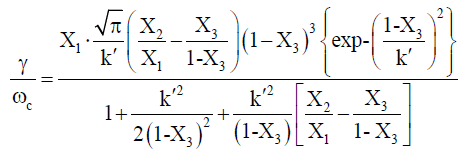 (21)
(21)
The real part of eq. (20) is:
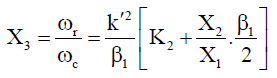 (22)
(22)
Where 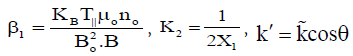 and
and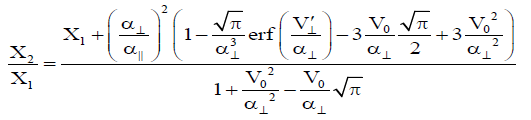
Plasma Parameters
Following plasma parameters have been adopted for the calculation of growth rate for the whistler instability in the magnetosphere. Ambient magnetic field Bo=2 × 10-7T, electron density no=5 × 106m-3 and magnitude of A.C electric field Eo=1 × 10-2V/m has been considered. Temperature anisotropy is supposed to vary from 1.25 to 1.75 and loss cone angle θ is to vary from 0° to 30°. Electron energy, KBT|| is taken to be 3KeV, 5KeV and 7KeV. According to this choice of plasma parameters, the explanations and details of the results are given as follows.
Discussion
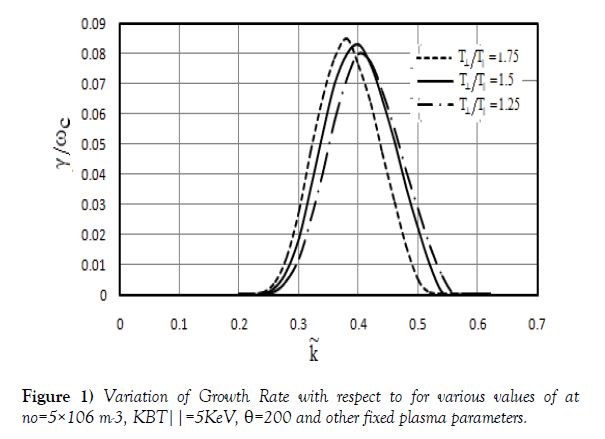
In Figure 1 dimensionless growth rate 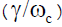 has been plotted for various values of
has been plotted for various values of 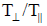 with respect to wave number. It basically shows the variation of temperature anisotropy
with respect to wave number. It basically shows the variation of temperature anisotropy 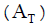 as
as 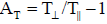 . As ratio of
. As ratio of 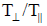 increases from 1.25 to 1.75, growth rate increases from 0.079863 to 0.08499 with slight shift in wave number from 0.4 to 0.38. It shows that whistler mode waves have grown due to loss of perpendicular kinetic energy of ring electrons. It implies that temperature anisotropy act as a source of free energy for the amplification and propagation of waves. It has been shown that with increase in the temperature anisotropy, growth rate shows a significant increase [40]. Therefore, the minimum electric field strength is sufficient to trigger the whistle emission and increase the growth rate.
increases from 1.25 to 1.75, growth rate increases from 0.079863 to 0.08499 with slight shift in wave number from 0.4 to 0.38. It shows that whistler mode waves have grown due to loss of perpendicular kinetic energy of ring electrons. It implies that temperature anisotropy act as a source of free energy for the amplification and propagation of waves. It has been shown that with increase in the temperature anisotropy, growth rate shows a significant increase [40]. Therefore, the minimum electric field strength is sufficient to trigger the whistle emission and increase the growth rate.
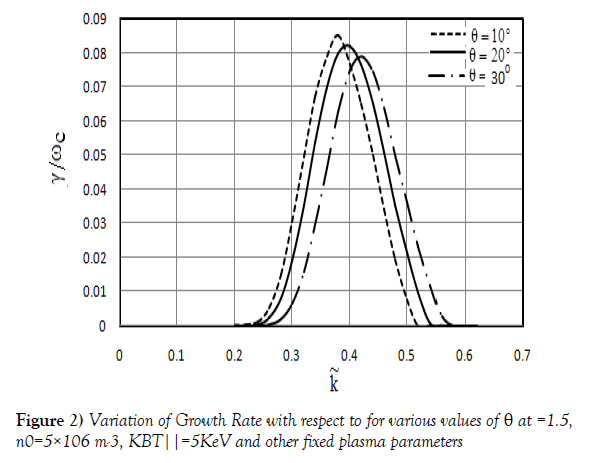
Figure 2 shows the variation in growth rate of whistler mode waves with respect to wave number for different values of propagation angle (θ). The study considers propagation of these waves at an angle of 10o , 20o and 30o with respect to ambient magnetic field of Earth. This figure shows that the growth rate decreases with increasing value of loss cone angle and shifting the bandwidth for higher order of loss cone angle. The maximum growth rate decreases from 0.084985 to 0.079034 as the angle of propagation changes from 10 o to 30 o with k shifting from 0.38 to 0.42. It means that the loss cone angle does not provide sufficient energy to produce the instabilities and propagation of waves. This result is in agreement with the result shown by [41], they concluded that there will be decrease in the growth rate as the wave becomes more oblique either due to landau damping or cyclotron resonant frequency and the broadness of frequency range increases.
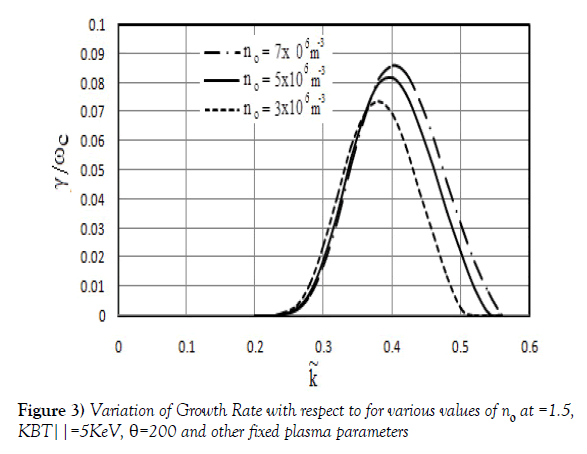
Figure 3 shows the graph with growth rate of whistler mode waves versus wave number for different values of number density. In Figure 3, the growth rate changes from 0.073547 to 0.085959 for increasing value of number density from 3 x 106 m-3 to 7 x 106 m-3 with wave number changing from 0.38 to 0.0.4. Therefore, as the number density of electrons in plasma regime increases growth rate of whistler mode waves increases.
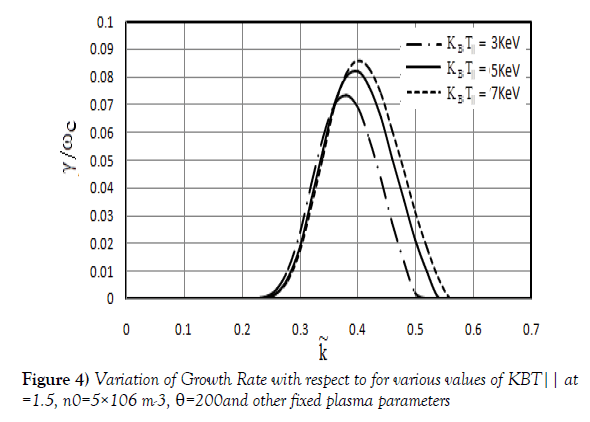
Figure 4 shows the change in dimensionless growth rate 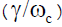 for different values of energy density
for different values of energy density 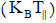 of electrons. The electron temperature varies from about 3KeV to 7KeV. Therefore, the growth rate of whistler waves has been calculated in the same range of energy density in the present paper. In Figure 4, the maximum growth rate calculated as 0.074457, 0.082843 and 0.086059 with a peak value at wave number 0.38, 0.4 and 0.4 respectively. It is observed that growth rate increases by increasing the thermal energy and the bandwidth increases for the higher order of
of electrons. The electron temperature varies from about 3KeV to 7KeV. Therefore, the growth rate of whistler waves has been calculated in the same range of energy density in the present paper. In Figure 4, the maximum growth rate calculated as 0.074457, 0.082843 and 0.086059 with a peak value at wave number 0.38, 0.4 and 0.4 respectively. It is observed that growth rate increases by increasing the thermal energy and the bandwidth increases for the higher order of 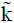 . This implies emission is possible for extended values of
. This implies emission is possible for extended values of 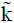 . So it can be seen that the energy density of electrons is one of the important parameters affecting the growth rate of whistler mode waves.
. So it can be seen that the energy density of electrons is one of the important parameters affecting the growth rate of whistler mode waves.
Conclusion
This paper presents the parametric analysis of growth rate of whistler mode waves in the magnetosphere of Earth using ring distribution function. Numerical calculations were performed by considering the kinetic approach and applying the characteristic solution method. The derivation expressions of the dispersion relation and the growth rate of the whistler waves propagated obliquely along the ambient magnetic field are analyzed. Detailed studies show that the growth rate of electromagnetic whistle mode waves increases with the increase of temperature anisotropy. This can also be used to study various instabilities in the planetary magnetosphere. The graphs show that temperature anisotropy acts as a source of free energy in the magnetosphere of Earth. Also increase in number density and energy density of the electrons increases growth rate of whistler waves. It can be said that loss of perpendicular kinetic energy is the cause of whistler mode waves.
Acknowledgement
The authors are grateful to the Founder president Dr. Ashok K. Chauhan Amity University, Dr. Atul Chauhan (President, Amity University) and Dr. Balvinder Shukla (Vice Chancellor, Amity University) for their immense encouragement. We also express our gratitude to the reviewers for their expert comments for the manuscript.
REFERENCES
- Tsurutani BT, Lakhina GS. Revs Geophys. 1997;35:491.
- Benson RF, Desch MD, Hunsucker RD, et al. J Geophys Res. 1988;93:277.
- Wu CS, Yoon PH, Freund HP. 1989;16:1461.
- Burtis WJ, Helliwell RA. Banded chorus: A new type of VLF radiation observed in the magnetosphere by OGO 1 and OGO 3. J Geophys Res. 1969;74(11):3002-10.
- Neubauer FM, Musmann G, Dehmel G. Fast magnetic fluctuations in the solar wind: Helios 1. J Geophys Res. 1977;82:3201-3212.
- Wilson LB III, Cattell CA, Kellogg PJ, et al. Low-frequency whistler waves and shocklets observed at quasi-perpendicular interplanetary shocks. J Geophys Res. 2009;114:A10106.
- Hoppe MM, Russell CT, Frank LA, et al. Upstream hydromagnetic waves and their association with backstreaming ion populations: ISEE 1 and 2 observations. J Geophys Res. 1981;86:4471-4492.
- Tsurutani BT, Thorne RM, Smith EJ, et al. Steepened magnetosonic waves at comet Giacobini-Zinner. J Geophys Res. 1987;92:11074-82.
- Moullard O, Masson A, Laakso H, et al. Density modulated whistler mode emissions observed near the plasmapause. Geophys Res Lett. 2002;29(20).
- Haque N, Inan US, Bell TF, et al. Cluster observations of whistler mode ducts and banded chorus. Geophys Res Lett. 2011;38:(L18107).
- Bell TF, Ngo HD. Electrostatic lower hybrid waves excited by electromagnetic whistler mode waves scattering from planar magnetic-field-aligned plasma density irregularities. J Geophys Res. 1990;95(A1):149-72.
- Pandey RP, Singh KK, Singh KM, et al. A theoretical study of whistler mode instability at uranian bow Shock. Earth Moon and Planets (The Netherlands). 2001;87:59-71.
- Helliwell RA. A Theory of Discrete VLF Emissions from the Magnetosphere. J Geophys Res. 1967;72:4773.
- Kennel CF, Petschek HE. Limit on stably trapped particle fluxes, J. Geophys. Res. 1966;71:1-28.
- Lyons LR, Thorne RM, Kennel CF. Pitch-angle diffusion of radiation belt electrons within the plasmasphere. J Geophys Res. 1972;77:3455-74.
- Inan US, Bell TF, Helliwell RA. Nonlinear pitch angle scattering of energetic electrons by coherent VLF waves in magnetosphere. J Geophys Res. 1978;83:3235.
- Huang JG, Hawkins, Lee LC. On the Generation of the Pulsating Aurora by the Loss Cone Driven Whistler Instability in the Equatorial Region. J Geophys Res. 1990;95:3893.
- Meredith NP, Horne RB, Anderson RR. Substorm dependence of chorus amplitudes: Implications for the acceleration of electrons to relativistic energies. J Geophys Res. 2001;106:165-173.
- Horne RB, Thorne RM, Glauert SA et al. Timescale for radiation belt electron acceleration by whistler mode chorus waves. J Geophys Res. 2005;110:A03225.
- Horne RB, Glauert SA, Thorne RM. Resonant diffusion of radiation belt electrons by whistle-mode chorus. Geophys Res Lett. 2003;30(9):1493.
- Cattell C. Discovery of very large amplitude whistler-mode waves in Earth’s radiation belts. Geophys Res Lett. 2008;41:L01105.
- Kellogg PJ, Cattell CA, Goetz K, et al. Electron trapping and charge transport by large amplitude whistlers. Geophys Res Lett. 2010;37:L20106.
- Cully CM, Bonnell JW, Ergun RE. THEMIS observations of long-lived regions of large-amplitude whistler waves in the inner magnetosphere. Geophys Res Lett. 2008;35:L17S16.
- Omura Y, Furuya N, Summers D. Relativistic turning acceleration of resonant electrons by coherent whistler mode waves in a dipole magnetic field. J Geophys Res. 2007;112: A06236.
- Bortnik J, Thorne RM, Inan US. Nonlinear interaction of energetic electrons with large amplitude chorus. Geophys Res Lett. 2008;35:L21102.
- Sharma OP, Patel VL. Low-frequency electromagnetic waves driven by gyrotropic gyrating beams. J Geophys Res. 1986;91: 1529.
- Goldstein ML, Wong NK. A theory for Low-frequency waves observed at comet Ciiacobini-Zinner. J Geophys Res. 1987;92: 469.
- Wu CS, Krauss-Varban D, Huo TS. A mirror instability associated with newly created ions in a moving plasma. J Geophys Res. 1988;93:11527.
- Gary SP, Madland CD. Electromagnetic ion instabilities in a cometary environment. J Geophys Res. 1988;93:235.
- Killen K, Omidi N, Krauss-Varban D, et al. Linear and nonlinear properties of ULF waves driven by ring-beam distribution functions. J Geophys Res. 1995;100:5835.
- Gray PC, Smith CW, Matthaeus WH, et al. Heating of the solar wind by pickup ion Alfvén ion cyclotron instability. Geophys Res Lett. 1996;23:113.
- Vandas M, Hellinger P. Liner dispersion properties of ring velocity distribution functions. Physics of Plasma. 2015;22: 062107.
- Umeda T, Ashour-Abdalla M, Schriver D, et al. Particle-in-cell simulation of Maxwellian ring velocity distribution. J Geophys Res. 2007;112:A04212.
- Frank LA, Burek BG, Ackerson KL et al. Plasmas in Saturn's magnetosphere. J Geophys Res. 1980;85(A11):5695.
- Lee YC, Kaw PK. Parametric instabilities of ion cyclotron waves in a plasma. Phys Fluids. 1972;15:911.
- Kumari J, Kaur R, Pandey RS. Effect of hot injection on electromagnetic ion cyclotron waves in inner magnetosphere of Saturn. Astrophys Space Sci. 2018;363:33.
- Kaur R, Pandey RS. Study of whistler mode waves for ring distribution function in Saturn’s magnetosphere. Advances in Space Research. 2017;59:2434-41.
- Wu CS, Yoon PH, Freund HP. A theory of electron cyclotron waves generated along auroral field lines observed by ground facilities. Geophys Res Lett. 1989;16(12):1461.
- Kumar S, Singh SK, Gwal AK. Effect of upflowing field-aligned electron beams on the electron cyclotron waves in the auroral magnetosphere. Pramana J Phys. 2007;68(4):611.
- Pandey RS, Kaur R, Bhadoria S, et al. Study of Whistler Mode Waves for Loss Cone Distribution Function with Perpendicular AC Electric Field in Magnetosphere. Astron Space Sci. 2016;2:009.
- Zhou Q, Xiao F, Shi J, et al. Instability and propagation of EMIC waves in the magnetosphere by a kappa distribution. J Geophys Res. 2012;117:A06203.